【pytorch】使用pytorch构建线性回归模型-了解计算图和自动梯度

使用pytorch构建线性回归模型

线性方程的一般形式

衡量线性损失的一般形式-均方误差

pytorch中计算图的作用和优势

在 PyTorch 中，计算图（Computational Graph）是一种用于表示神经网络运算的数据结构。每个节点代表一个操作，例如加法、乘法或激活函数，而边则代表这些操作之间的数据流动。

计算图的主要优点是可以自动进行微分计算。当你在计算图上调用 .backward() 方法时，PyTorch 会自动计算出所有变量的梯度。这是通过使用反向传播算法来实现的，该算法从最后的输出开始，然后根据链式法则回溯到输入。

以下是一个简单的计算图示例：

import torch

# 定义两个张量
x = torch.tensor([1.0], requires_grad=True)
y = torch.tensor([2.0], requires_grad=True)

# 定义计算图
z = x * y
out = z.mean()

# 计算梯度
out.backward()

print(x.grad) # tensor([0.5])
print(y.grad) # tensor([0.5])

在这个例子中，我们首先定义了两个需要求导的张量 x 和 y。然后，我们定义了一个计算图，其中 z 是 x 和 y 的乘积，out 是 z 的平均值。当我们调用 out.backward() 时，PyTorch 会自动计算出 x 和 y 的梯度。

注意，只有那些设置了 requires_grad=True 的张量才会被跟踪并存储在计算图中。这样，我们就可以在需要时计算这些张量的梯度。

import torch

x_data = [1.0, 2.0, 3.0] #x输入，表示特征
y_data = [2.0, 4.0, 6.0] #y输入，表示标签

w = torch.tensor([1.0], requires_grad=True) #创建权重张量，启用自动计算梯度

def forward(x): #前向传播
    return x * w #特征和权重的点积，构建乘法计算图

def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2 #均方误差，构建损失计算图

线性模型的计算图的一般形式

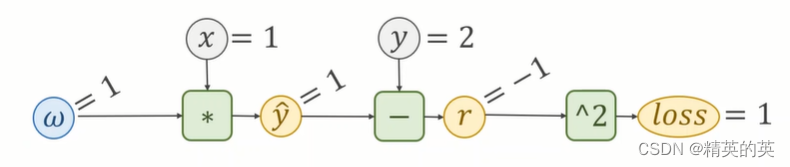
print("predict before training is {}".format(forward(4).item()))

for epoch in range(100):
    for x,y in zip(x_data, y_data):#组合特征和标签
        l = loss(x,y) #定义计算图，包括前向传播和计算损失
        l.backward() #反向传播，计算梯度
        print("\tgrad:", x,y,w.grad.item())#梯度的标量
        w.data = w.data - 0.01 * w.grad.data#使用“.data”表示是更新数据，而不是创建计算图
        w.grad.data.zero_()#梯度清零，准备创建下一个计算图
    print("progress:", epoch, l.item())
print("predict after training:{}".format(forward(4).item()))

使用pytorch API

pytorch的张量计算

准备数据集

x_data = torch.tensor([[1.0],[2.0],[3.0]])
y_data = torch.tensor([[2.0],[4.0],[6.0]])

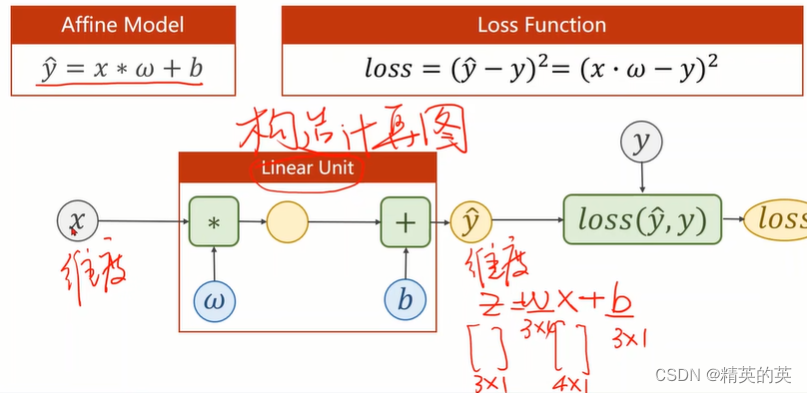
class LinearModel(torch.nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super(LinearModel, self).__init__(*args, **kwargs)
        self.linear = torch.nn.Linear(in_features=1, out_features=1)
        
    def forward(self, x):
        y_pred = self.linear(x)
                return y_pred
    
model = LinearModel()

定义损失函数和损失优化函数

关于小批量随机梯度下降

小批量随机梯度下降（Mini-batch Stochastic Gradient Descent）是批量梯度下降的一种变体。与批量梯度下降相比，小批量随机梯度下降在每次迭代时只使用一小部分数据（称为小批量）来计算梯度，然后根据这个梯度来更新模型的参数。

小批量随机梯度下降的目标函数为：

$$J(\theta )=\frac{1}{m}\sum _{i=1}^{m}L(y^{(i)},f_{\theta }(x^{(i)}))$$

其中，$J(\theta )$ 是目标函数，$m$ 是数据集的大小，$L(y^{(i)},f_{\theta }(x^{(i)}))$ 是第 $i$ 个样本的损失函数，$f_{\theta }(x^{(i)})$ 是模型对第 $i$ 个样本的预测。

小批量随机梯度下降的更新规则为：

$$\theta =\theta ?\alpha ?J(\theta )$$

其中，$\alpha$ 是学习率，$?J(\theta )$ 是目标函数关于 $\theta$ 的梯度。

小批量随机梯度下降的优点是它结合了批量梯度下降的优点（即可以利用整个数据集的信息来更新参数）和随机梯度下降的优点（即可以在每次迭代时使用新的数据）。这使得它在处理大规模数据集时具有更好的计算效率，同时也能避免随机梯度下降的问题（即可能会陷入局部最优）。

criteria = torch.nn.MSELoss()#使用均方误差做损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)#使用随机梯度下降做损失优化函数
for epoch in range(1000):
    y_pred = model(x_data)
    loss = criteria(y_pred, y_data)
    print(epoch, loss)
    optimizer.zero_grad()#梯度清零
    loss.backward()#反向传播
    optimizer.step()#梯度下降更新参数

预测

print("w=", model.linear.weight.item())
print("b=", model.linear.bias.item())

x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print("y_pred=", y_test.data)
print("w=", model.linear.weight.item())
print("b=", model.linear.bias.item())