盛最多水的容器（力扣11题）

例题：

分析：

这道题给出了一个数组，数组里的元素可以看成每一个挡板，要找到哪两个挡板之间盛的水最多，返回盛水量的最大值。这其实是一个双指针问题。

我们可以先固定第一个挡板( i )和最后一个挡板( j )，? height[0] = 1, height[8] = 7，看看盛水量。

现在盛水量比较少，要让盛水量尽可能多，假设我们先移动 j 指针

? ? ? ? ?

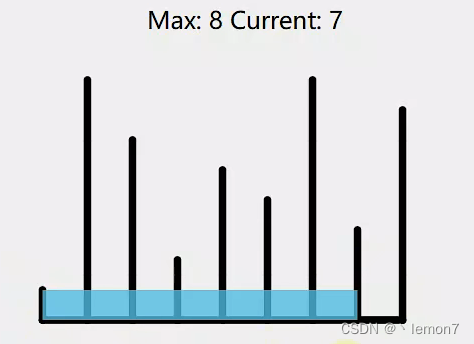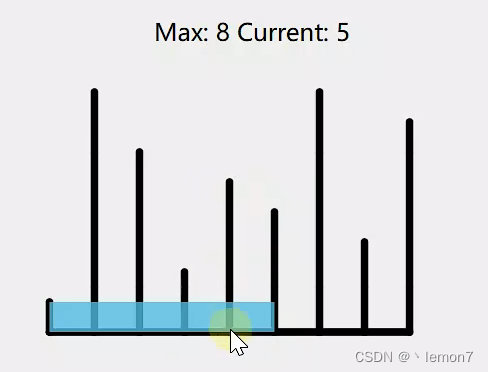
我们发现，固定了两个挡板，当移动高的挡板时，盛水量随着 j 指针的左移在不断减少，必然小于最初的盛水量，因此我们不能移动高挡板。

如果移动较低的挡板，如下图：

移动较低的挡板，盛水量是有可能增多的。

核心思想：向中间不断缩减距离，每次改变较短的挡板。

代码实现：

public class MostWaterLeetcode11 {

    public static int maxArea(int[] height) {
        int i = 0, j = height.length - 1;
        int max = 0;  //最大盛水量
        while(i < j){
            int min = Integer.min(height[i], height[j]);
            max = Math.max(max, (j - i) * min);
            while(i < j && height[i] <= min){
                i++;
            }
            while(i < j && height[j] <= min){
                j--;
            }
        }
        return max;
    }

    public static void main(String[] args) {
        System.out.println(maxArea(new int[]{1, 8, 6, 2, 5, 4, 8, 3, 7})); // 49
        System.out.println(maxArea(new int[]{2,1})); // 1
    }
}