认识&对比 React、Vue2、Vue3 三者的 diff 算法

React Diff 算法

认识 React Diff 算法

React 是 Fiber 架构的，Fiber 其实是一个链表的结构，但是由于没有设置反向指针，因此没有使用双端比对的方式去优化 Diff 算法（没有反向指针，从右往左遍历链表会很困难）。这一点在 React 源码 reconcileChildrenArray 函数的注释中也有说明。

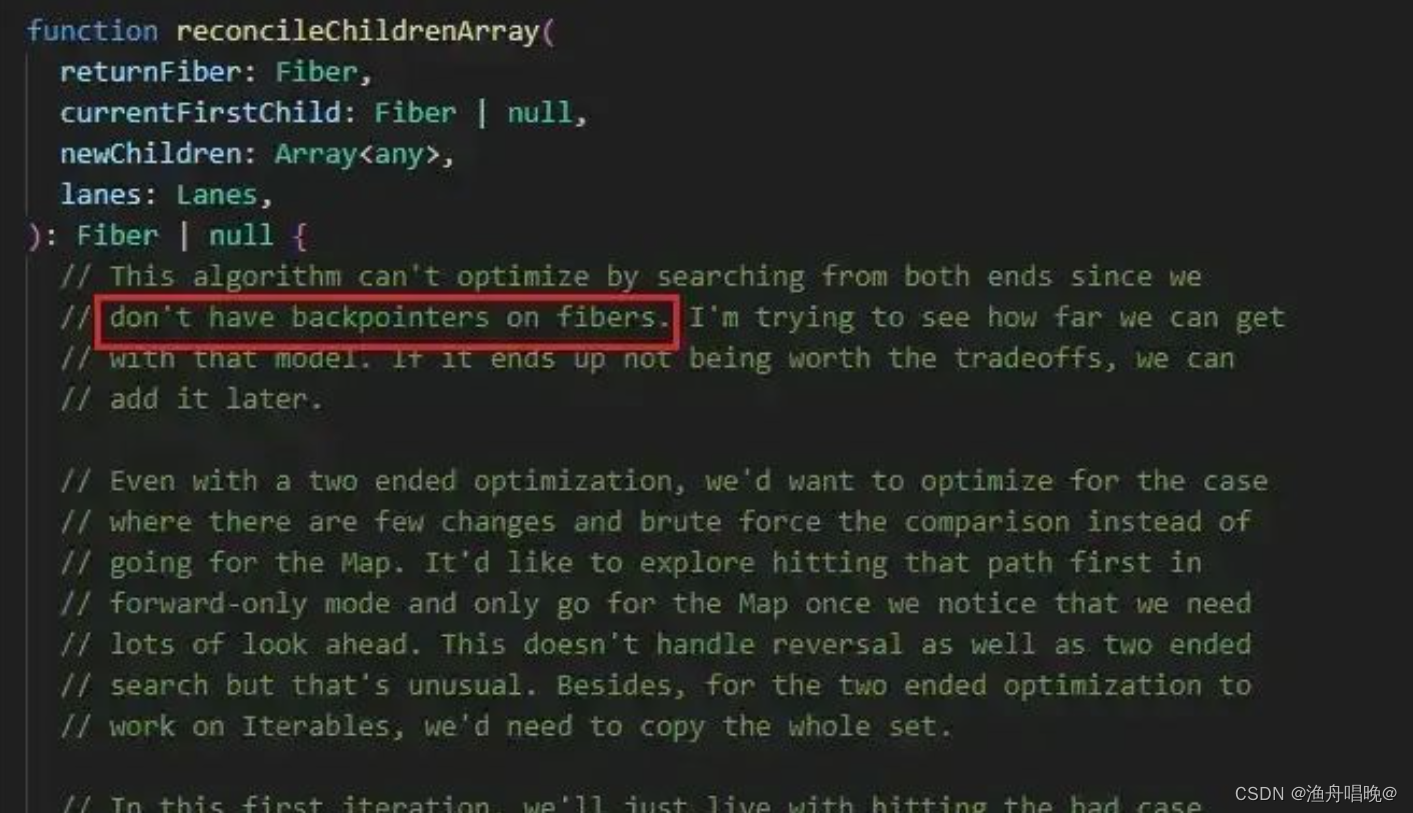
React 采用 Fiber 架构的原因是 JavaScript 的运行会阻塞页面的渲染，React 为了不阻塞页面的渲染，采用了 Fiber 架构，Fiber 也是一种链表的数据结构，基于这个数据结构可以实现由原来不可中断的更新过程变成异步的可中断的更新。

Fiber 节点的定义在 packages\react-reconciler\src\ReactFiber.old.js 文件中

function FiberNode(
  tag: WorkTag,
  pendingProps: mixed,
  key: null | string,
  mode: TypeOfMode,
) {
  // Instance
  this.tag = tag;
  this.key = key;
  this.elementType = null;
  this.type = null;
  this.stateNode = null;

  // Fiber
  this.return = null;
  this.child = null;
  this.sibling = null;
  this.index = 0;

  this.ref = null;

  this.pendingProps = pendingProps;
  this.memoizedProps = null;
  this.updateQueue = null;
  this.memoizedState = null;
  this.dependencies = null;

  this.mode = mode;

  // Effects
  this.flags = NoFlags;
  this.nextEffect = null;

  this.firstEffect = null;
  this.lastEffect = null;

  this.lanes = NoLanes;
  this.childLanes = NoLanes;

  this.alternate = null;

  // 省略一些无关的属性...
}
上面的代码摘自 React 17.0.0 版本

从上面的实现来看，FiberNode 的定义挺复杂的，有那么多的属性。笔者个人认为，也是因为 Fiber 的复杂，增加了阅读 React 源码的心智负担。下面来分析一下 FiberNode 中各个属性的作用。

tag ，表示节点类型的标记，例如 FunctionComponent 、ClassComponent 等。

tag 为 WorkTag 类型，WorkTag 的定义可在 packages\react-reconciler\src\ReactWorkTags.js 文件中查看。WorkTag 的完整定义为

export const FunctionComponent = 0;
export const ClassComponent = 1;
// Before we know whether it is function or class
export const IndeterminateComponent = 2; 
// Root of a host tree. Could be nested inside another node.
export const HostRoot = 3; 
// A subtree. Could be an entry point to a different renderer.
export const HostPortal = 4; 
export const HostComponent = 5;
export const HostText = 6;
export const Fragment = 7;
export const Mode = 8;
export const ContextConsumer = 9;
export const ContextProvider = 10;
export const ForwardRef = 11;
export const Profiler = 12;
export const SuspenseComponent = 13;
export const MemoComponent = 14;
export const SimpleMemoComponent = 15;
export const LazyComponent = 16;
export const IncompleteClassComponent = 17;
export const DehydratedFragment = 18;
export const SuspenseListComponent = 19;
export const FundamentalComponent = 20;
export const ScopeComponent = 21;
export const Block = 22;
export const OffscreenComponent = 23;
export const LegacyHiddenComponent = 24;

key ，节点的唯一标识符，用于进行节点的 diff 和更新。

elementType ，大部分情况与 type 相同，某些情况不同，比如 FunctionComponent 使用 React.memo 包裹，表示元素的类型

type ，表示元素的类型， 对于 FunctionComponent，指函数本身，对于ClassComponent，指 class，对于 HostComponent，指 DOM 节点 tagName

stateNode ，FiberNode 对应的真实 DOM 节点

return ，指向该 FiberNode 的父节点
child ，指向该 FiberNode 的第一个子节点
sibling ，指向右边第一个兄弟 Fiber 节点
index ，当前节点在父节点的子节点列表中的索引

ref ，存储 FiberNode 的引用信息，与 React 的 Ref 有关。使用 ref 引用值[1]

pendingProps ，表示即将被应用到节点的 props 。当父组件发生更新时，会将新的 props 存储在 pendingProps 中，之后会被应用到节点。

memoizedProps，表示节点上一次渲染的 props 。在完成本次更新之前，memoizedProps 中存储的是上一次渲染时的 props ，用于对比新旧 props 是否发生变化。

updateQueue，用于存储组件的更新状态，比如新的状态、属性或者 context 的变化。通过 updateQueue ，React 可以跟踪组件的更新并在合适的时机执行更新。

memoizedState ，类组件保存上次渲染后的 state ，函数组件保存的 hooks 信息。

dependencies ，存储节点的依赖信息，用于处理 useEffect 等情况。

mode ，表示节点的模式，如 ConcurrentMode 、StrictMode 等。

以下是关于节点副作用（Effect）的属性：

flags ，存储 FiberNode 的标记，表示节点上的各种状态和变化（删除、新增、替换等）。flags 的定义在 packages\react-reconciler\src\ReactFiberFlags.js 文件中，flags 为 number 类型。

nextEffect ，指向下一个有副作用的节点。

firstEffect，指向节点的第一个有副作用的子节点。

lastEffect，指向节点的最后一个有副作用的子节点。

由于 React 无法使用双端比对的方法来优化 Diff 算法，所以 React 在进行多节点 Diff 的时候需要进行两轮遍历。

第一轮遍历：处理 更新 的节点。

第二轮遍历：处理剩下的不属于 更新 的节点。

React 多节点的 Diff 算法的实现在 reconcileChildrenArray 函数中

function reconcileChildrenArray(
  returnFiber: Fiber,
  currentFirstChild: Fiber | null,
  newChildren: Array<*>,
  lanes: Lanes,
): Fiber | null {
  // This algorithm can't optimize by searching from both ends since we
  // don't have backpointers on fibers. I'm trying to see how far we can get
  // with that model. If it ends up not being worth the tradeoffs, we can
  // add it later.

  // Even with a two ended optimization, we'd want to optimize for the case
  // where there are few changes and brute force the comparison instead of
  // going for the Map. It'd like to explore hitting that path first in
  // forward-only mode and only go for the Map once we notice that we need
  // lots of look ahead. This doesn't handle reversal as well as two ended
  // search but that's unusual. Besides, for the two ended optimization to
  // work on Iterables, we'd need to copy the whole set.

  // In this first iteration, we'll just live with hitting the bad case
  // (adding everything to a Map) in for every insert/move.

  // If you change this code, also update reconcileChildrenIterator() which
  // uses the same algorithm.

  if (__DEV__) {
    // First, validate keys.
    let knownKeys = null;
    for (let i = 0; i < newChildren.length; i++) {
      const child = newChildren[i];
      knownKeys = warnOnInvalidKey(child, knownKeys, returnFiber);
    }
  }

  let resultingFirstChild: Fiber | null = null;
  let previousNewFiber: Fiber | null = null;

  let oldFiber = currentFirstChild;
  let lastPlacedIndex = 0;
  let newIdx = 0;
  let nextOldFiber = null;
  for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {
    if (oldFiber.index > newIdx) {
      nextOldFiber = oldFiber;
      oldFiber = null;
    } else {
      nextOldFiber = oldFiber.sibling;
    }
    const newFiber = updateSlot(
      returnFiber,
      oldFiber,
      newChildren[newIdx],
      lanes,
    );
    if (newFiber === null) {
      // TODO: This breaks on empty slots like null children. That's
      // unfortunate because it triggers the slow path all the time. We need
      // a better way to communicate whether this was a miss or null,
      // boolean, undefined, etc.
      if (oldFiber === null) {
        oldFiber = nextOldFiber;
      }
      break;
    }
    if (shouldTrackSideEffects) {
      if (oldFiber && newFiber.alternate === null) {
        // We matched the slot, but we didn't reuse the existing fiber, so we
        // need to delete the existing child.
        deleteChild(returnFiber, oldFiber);
      }
    }
    lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
    if (previousNewFiber === null) {
      // TODO: Move out of the loop. This only happens for the first run.
      resultingFirstChild = newFiber;
    } else {
      // TODO: Defer siblings if we're not at the right index for this slot.
      // I.e. if we had null values before, then we want to defer this
      // for each null value. However, we also don't want to call updateSlot
      // with the previous one.
      previousNewFiber.sibling = newFiber;
    }
    previousNewFiber = newFiber;
    oldFiber = nextOldFiber;
  }

  if (newIdx === newChildren.length) {
    // We've reached the end of the new children. We can delete the rest.
    deleteRemainingChildren(returnFiber, oldFiber);
    return resultingFirstChild;
  }

  if (oldFiber === null) {
    // If we don't have any more existing children we can choose a fast path
    // since the rest will all be insertions.
    for (; newIdx < newChildren.length; newIdx++) {
      const newFiber = createChild(returnFiber, newChildren[newIdx], lanes);
      if (newFiber === null) {
        continue;
      }
      lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
      if (previousNewFiber === null) {
        // TODO: Move out of the loop. This only happens for the first run.
        resultingFirstChild = newFiber;
      } else {
        previousNewFiber.sibling = newFiber;
      }
      previousNewFiber = newFiber;
    }
    return resultingFirstChild;
  }

  // Add all children to a key map for quick lookups.
  const existingChildren = mapRemainingChildren(returnFiber, oldFiber);

  // Keep scanning and use the map to restore deleted items as moves.
  for (; newIdx < newChildren.length; newIdx++) {
    const newFiber = updateFromMap(
      existingChildren,
      returnFiber,
      newIdx,
      newChildren[newIdx],
      lanes,
    );
    if (newFiber !== null) {
      if (shouldTrackSideEffects) {
        if (newFiber.alternate !== null) {
          // The new fiber is a work in progress, but if there exists a
          // current, that means that we reused the fiber. We need to delete
          // it from the child list so that we don't add it to the deletion
          // list.
          existingChildren.delete(
            newFiber.key === null ? newIdx : newFiber.key,
          );
        }
      }
      lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
      if (previousNewFiber === null) {
        resultingFirstChild = newFiber;
      } else {
        previousNewFiber.sibling = newFiber;
      }
      previousNewFiber = newFiber;
    }
  }

  if (shouldTrackSideEffects) {
    // Any existing children that weren't consumed above were deleted. We need
    // to add them to the deletion list.
    existingChildren.forEach(child => deleteChild(returnFiber, child));
  }

  return resultingFirstChild;
}

上面的代码摘自 React 17.0.0 版本，为了让读者看到原汁原味的源码，笔者没有删除源码中的注释，但是在后面的讲解中，会删掉一些无关的代码。

首先看一下 reconcileChildrenArray 函数各入参的函数

function reconcileChildrenArray(
  returnFiber: Fiber,
  currentFirstChild: Fiber | null,
  newChildren: Array<*>,
  lanes: Lanes,
) {
  // 省略...
}

• returnFiber ，currentFirstChild 的父级 fiber 节点
• currentFirstChild ，当前执行更新任务的 fiber 节点
• newChildren ，组件的 render 方法渲染出的新的 ReactElement 节点
• lanes，与优先级相关，在这里可以先不深究

第一轮遍历，从头开始遍历 newChildren ，逐个与 oldFiber 链中的节点进行比较，判断 DOM 节点是否可复用。如果节点的 key 不同，则不可复用，直接跳出循环，第一轮遍历结束。如果 key 相同，但是 type 不同，则会重新创建节点，将 oldFiber 标记为 Deletion ，并继续遍历。

let lastPlacedIndex = 0;
let newIdx = 0;
let nextOldFiber = null;

for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {
  if (oldFiber.index > newIdx) {
    nextOldFiber = oldFiber;
    oldFiber = null;
  } else {
    nextOldFiber = oldFiber.sibling;
  }
  // 生成新的节点，判断 key 与 type 是否相同就在 updateSlot 中
  // 只有 key 和 type 都相同才会复用 oldFiber 节点
  const newFiber = updateSlot(
    returnFiber,
    oldFiber,
    newChildren[newIdx],
    lanes,
  );
  if (newFiber === null) {
    // key 不同，newFiber 会为 null ，直接跳出循环，第一轮遍历结束
    if (oldFiber === null) {
      oldFiber = nextOldFiber;
    }
    break;
  }
  if (shouldTrackSideEffects) {
    if (oldFiber && newFiber.alternate === null) {
      // key 相同，但是 type 不同的情况，将 oldFiber 打上 Deletion 的标记
      deleteChild(returnFiber, oldFiber);
    }
  }
  // 记录最后一个可复用的节点在 oldFiber 中的位置索引
  lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
  if (previousNewFiber === null) {
    resultingFirstChild = newFiber;
  } else {
    previousNewFiber.sibling = newFiber;
  }
  previousNewFiber = newFiber;
  oldFiber = nextOldFiber;
}

lastPlacedIndex 是最后一个可复用的节点在 oldFiber 中的位置索引，用于后续判断节点是否需要复用。

第一轮遍历完毕后，会有以下几种情况：

1. newChildren 与 oldFiber 同时遍历完
2. newChildren 没遍历完，oldFiber 遍历完
3. newChildren 遍历完，oldFiber 没遍历完
4. newChildren 与 oldFiber 都没遍历完

newChildren 与 oldFiber 同时遍历完，这个是最理想的情况，只需在第一轮遍历进行组件 更新，此时 Diff 结束。

newChildren 没遍历完，oldFiber 遍历完，这说明 newChildren 中剩下的节点都是新插入的节点，只需遍历剩下的 newChildren 创建新的 Fiber 节点并以此标记为 Placement 。相关代码逻辑如下 👇

if (oldFiber === null) {
  // 遍历剩余的 newChildren
  for (; newIdx < newChildren.length; newIdx++) {
    // 创建新的 Fiber 节点
    const newFiber = createChild(returnFiber, newChildren[newIdx], lanes);
    if (newFiber === null) {
      continue;
    }
    // 将新的 Fiber 节点标记为 Placement
    lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
    // 将新的 Fiber 节点用 silbing 指针连接成链表
    if (previousNewFiber === null) {
      resultingFirstChild = newFiber;
    } else {
      previousNewFiber.sibling = newFiber;
    }
    previousNewFiber = newFiber;
  }
  // 返回新的 Fiber 节点组成的链表的头部节点
  return resultingFirstChild;
}

newChildren 遍历完，oldFiber 没遍历完，意味着本次更新比之前的节点数量少，有节点被删除了。所以需要遍历剩下的 oldFiber ，依次标记 Deletion 。相关代码逻辑如下 👇

if (newIdx === newChildren.length) {
  // 遍历剩下的 oldFiber 并标记为 Deletion
  deleteRemainingChildren(returnFiber, oldFiber);
  return resultingFirstChild;
}

function deleteRemainingChildren(
  returnFiber: Fiber,
  currentFirstChild: Fiber | null,
): null {
  if (!shouldTrackSideEffects) {
    return null;
  }

  let childToDelete = currentFirstChild;
  while (childToDelete !== null) {
    deleteChild(returnFiber, childToDelete);
    childToDelete = childToDelete.sibling;
  }
  return null;
}

function deleteChild(returnFiber: Fiber, childToDelete: Fiber): void {
  if (!shouldTrackSideEffects) {
    // Noop.
    return;
  }
  const deletions = returnFiber.deletions;
  if (deletions === null) {
    returnFiber.deletions = [childToDelete];
    returnFiber.flags |= Deletion;
  } else {
    deletions.push(childToDelete);
  }
}

newChildren 与 oldFiber 都没遍历完，这是 Diff 算法最难的部分。

newChildren 与 oldFiber 都没遍历完，则有可能存在移动了位置的节点，所以为了快速地找到 oldFiber 中可以复用的节点，则创建一个以 oldFiber 的 key 为 key ，oldFiber 为 value 的 Map 数据结构。

// Add all children to a key map for quick lookups.
const existingChildren = mapRemainingChildren(returnFiber, oldFiber);

function mapRemainingChildren(
  returnFiber: Fiber,
  currentFirstChild: Fiber,
): Map<string | number, Fiber> {
  // Add the remaining children to a temporary map so that we can find them by
  // keys quickly. Implicit (null) keys get added to this set with their index
  // instead.
  const existingChildren: Map<string | number, Fiber> = new Map();

  let existingChild = currentFirstChild;
  while (existingChild !== null) {
    if (existingChild.key !== null) {
      existingChildren.set(existingChild.key, existingChild);
    } else {
      existingChildren.set(existingChild.index, existingChild);
    }
    existingChild = existingChild.sibling;
  }
  return existingChildren;
}
然后会遍历剩余的 newChildren ，逐个在 map 中寻找 oldFiber 中可复用的节点，如果找到可复用的节点，则将 oldIndex 与 lastPlacedIndex 比较，如果 oldIndex 与 lastPlacedIndex 小，则该节点需要右移，将新的 Fiber 节点标记为 Placement 。否则，将 lastPlacedIndex 更新为 oldIndex 。

遍历完 newChildren 后，map 中还有节点剩余，则那些节点属于多余的节点，需要标记为删除（Deletion）。

// 遍历 newChildren
for (; newIdx < newChildren.length; newIdx++) {
  // 在 map 中查找在 oldFiber 中可复用的节点
  const newFiber = updateFromMap(
    existingChildren,
    returnFiber,
    newIdx,
    newChildren[newIdx],
    lanes,
  );  
  if (newFiber !== null) {
    // 找到了可复用的 Fiber 节点
    if (shouldTrackSideEffects) {
      if (newFiber.alternate !== null) {
        // 将其从 map 中删除，因为该节点已经被复用了，
        // 继续留在 map 中会被当做剩余的节点被删除
        existingChildren.delete(
          newFiber.key === null ? newIdx : newFiber.key,
        );
      }
    }
    // 更新最后一个可复用节点节点的位置索引
    lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
    // 将 newFiber 用 sibling 连接成单链表
    if (previousNewFiber === null) {
      resultingFirstChild = newFiber;
    } else {
      previousNewFiber.sibling = newFiber;
    }
    previousNewFiber = newFiber;
  }
}

if (shouldTrackSideEffects) {
  // 遍历完 newChildren 后，还存在 map 在的节点就是剩余的节点，需要被删除
  existingChildren.forEach(child => deleteChild(returnFiber, child));
}

// 返回新的 fiber 链表
return resultingFirstChild;
上面讲了很多 Diff 的理论，接下来会介绍实战的案例，来理解 React Diff 的流程。

React Diff 案例
假设：

oldFiber 链表为 abcd

newFiber 链表为 dabc

第一轮遍历开始，a 与 d 比对，key 改变，不可复用，跳出遍历，第一轮遍历结束。

第二轮遍历开始，由于新的 Fiber 节点和旧的 Fiber 节点都有剩余，因此不会执行删除旧节点与插入新节点的操作。

首先，将 oldFiber （abcd）保存为 map

继续遍历剩余的 newFiber （dabc）节点

key === d 在 map 中存在，即在 oldFiber 中存在，此时记为 oldIndex 为 3。

比较 oldIndex 与 lastPlacedIndex

oldIndex 3 > lastPlacedIndex 0

则更新 lastPlacedIndex = 3

d 节点位置不变

继续遍历剩余 newFiber 节点

（当前 oldFiber ：abc ，newFiber ：abc）

同理，key === a 在 oldFiber 中存在

记 oldIndex 为 a 在 oldFiber 链表中的索引 0，oldIndex === 0

比较 oldIndex 与 lastPlacedIndex

oldIndex 0 < lastPlacedIndex 3

则 a 节点需要向右移动

继续遍历剩余 newFiber 节点，

（当前 oldFiber：bc，newFiber：bc）

同理，key === b 在 oldFiber 中存在

记 oldIndex 为 b 在 oldFiber 链表中的索引 1，oldIndex === 1

比较 oldIndex 与 lastPlacedIndex

oldIndex 1 < lastPlacedIndex 3

则 b节点需要向右移动

继续遍历剩余 newFiber ，

（当前 oldFiber ：c ，newFiber : c）

同理，key === c 在 oldFiber 中存在

记 oldIndex 为 c 在 oldFiber 链表中的索引 2，oldIndex === 2

比较 oldIndex 与 lastPlacedIndex

oldIndex 2 < lastPlacedIndex 3

则 c节点需要向右移动。

至此，第二轮遍历结束。

通过上面 Diff 的流程可知，React 将 abcd 更新为 dabc ，是保持 d 不变，将 abc 分别移动到了 d 后面。

因此，从性能的角度触发，要尽量减少将节点从后面移动到前端的操作。

lastPlacedIndex：最后一个可复用节点的在 oldFiber 中的位置索引

oldIndex：当前遍历到的 oldFiber 节点在 oldFiber 中的位置索引

React 会调用 updateSlot 方法，在 updateSlot 中判断 fiber 节点能否复用，只要是 key 相同，updateSlot 都会返回 newFiber ，key 不同，则会返回 null ，第 1 轮遍历结束。

Vue2 与 React Diff 的区别
认识 Vue2 Diff 算法
Vue2 采用了双端 Diff 算法，算法流程主要是：

对比头头、尾尾、头尾、尾头是否可以复用，如果可以复用，就进行节点的更新或移动操作。
如果经过四个端点的比较，都没有可复用的节点，则将就的子序列保存为节点 key 为 key ，index 为 value 的 map 。
拿新的一组子节点的头部节点去 map 中查找，如果找到可复用的节点，则将相应的节点进行更新，并将其移动到头部，然后头部指针右移。
然而，拿新的一组子节点中的头部节点去旧的一组子节点中寻找可复用的节点，并非总能找到，这说明这个新的头部节点是新增节点，只需要将其挂载到头部即可。
经过上述处理，最后还剩下新的节点就批量新增，剩下旧的节点就批量删除。
Vue2 Diff 案例
假设

旧子序列为：abcd

新子序列为：dabc

头头比较：a vs d ，key 不相同，不可复用

尾尾比较：d vs c ，key 不相同，不可复用

头尾比较：a vs c ，key 不相同，不可复用

尾头比较：d vs d ，key 相同，可以复用，将 d 节点移动到头部

旧子序列的尾部指针左移，新子序列的头部指针右移。

然后会继续进行双端比对，发现 a 、b 、c 三个节点都只需要更新，不需要移动位置。

最后比较新子序列的头部指针与尾部指针、旧子序列的头部指针与尾部指针，发现没有遗留新节点，也没有遗留旧节点，不需要执行批量新增新节点与批量删除旧节点的操作

Diff 流程结束。

可以发现 Vue2 在处理 abcd 更新为 dabc 的时候，只移动了 1 次位置，而 React 却要移动三次。

Vue 与 React 有类似的地方，就是 key 和 tag（标签）都相同，才可复用，如果 tag 不同，则会创建一个新的 dom 节点。在本案例中，为方便理解，未考虑 tag 不同的情况

当然，这并不能说 Vue2 比 React 要好，而是要从整体出发，这两个框架各有优势，目前还无法说明孰优孰劣。当然，目前从性能这个单一的角度来看，Vue2 更占优一些。

区别

Vue2 的 Diff 与 React 的 Diff 主要区别为：

Vue2 采用双端比对的方式优化了 Diff 算法，而 React 由于是 Fiber 架构，是单链表，没有使用双端比对的方式优化
Vue2 在 Diff 的时候与 React 在 Diff 的时候都采用了 map 来加快查找的效率，但是 Vue2 构造的 Diff 是 key -> index 的映射，而 React 构造的 Diff 是 key -> Fiber节点 的映射
Vue3 与 React Diff 的区别
认识 Vue3 Diff 算法
Vue3 的 Diff 算法与 Vue2 的 Diff 算法一样，也会先进行双端比对，只是双端比对的方式不一样。Vue3 的 Diff 算法借鉴了字符串比对时的双端比对方式，即优先处理可复用的前置元素和后置元素。

Vue3 的 Diff 算法的流程如下

处理前置节点
处理后置节点
新节点有剩余，则挂载剩余的新节点
旧节点有剩余，则卸载剩余的旧节点
乱序情况（新、旧节点都有剩余），则构建最长递增子序列
节点在最长递增子序列中，则该节点不需移动
节点不在最长递增子序列中，则移动该节点
Vue3 Diff 案例
假设

旧子序列为：abcd

新子序列为：dabc

处理前置节点：a vs d ，key 不同，不可复用，退出前置节点的处理

处理后置节点：d vs c ，key 不同，不可复用，退出后置节点的处理

进入乱序的情况的处理，创建新旧节点下标映射，并根据这个映射构造最长递增子序列

然后发现 a、b、c 都在最长递增子序列中，不需要移动位置

最后将 d 移动到头部

Diff 流程结束。

可以发现 Vue3 在处理 abcd 更新为 dabc 的时候，也只移动了 1 次位置，而 React 却要移动三次。

当然，这也不能说 Vue3 比 React 要好，而是要从整体出发，这两个框架各有优势，目前还无法说明孰优孰劣。当然，目前从性能这个单一的角度来看，Vue3 更占优一些，同时也比 Vue2 要占优。

区别

Vue3 的 Diff 与 React 的 Diff 主要区别为：

Vue3 也采用了双端对比的方式优化了 Diff 算法，这一点与 Vue2 是类似的。
Vue3 还构造了最长递增子序列，最大程度降低了 DOM 操作，而 React 没有使用最长递增子序列来加速 Diff 算法

总结

通过 React 源码和 Vue 源码的对比学习，发现 React 源码比 Vue 源码难懂很多，个人觉得是由于 React 采用了 Fiber 架构造成的，Fiber 是一个链表结构，子节点之间通过 sibling 指针连接，没有 Vue 直接用数组来得那么简单直接。

Vue2 、Vue3 都采用了双端比对的方式来加速 Diff 算法，而 React 采用了单链表的数据结构来存储 Fiber 节点，导致其使用双端比对的方式来优化 Diff 算法变得困难，所以 React 没有采用双端比对的方式来优化，相比 Vue2 ，Vue3 采用了最长递增子序列更进一步地提升了 Diff 算法的性能。