leetcode 98. 验证二叉搜索树
题目
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:true
示例 2:
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
树中节点数目范围在[1, 104] 内
?
2
31
-2^{31}
?231 <= Node.val <=
2
31
?
1
2^{31} - 1
231?1
思路
其实一开始思路是正常往左右分别遍历并且判断当前根节点和左右子树的大小关系,但是WA了
class Solution {
public boolean isValidBST(TreeNode root) {
if (root.left == null && root.right == null) {return true;}
else if (root.left == null) {return root.val < root.right.val && isValidBST(root.right);}
else if (root.right == null) {return root.val > root.left.val && isValidBST(root.left);}
else {return root.val > root.left.val && root.val < root.right.val && isValidBST(root.left) && isValidBST(root.right);}
}
}
因为上面这个没考虑到情况
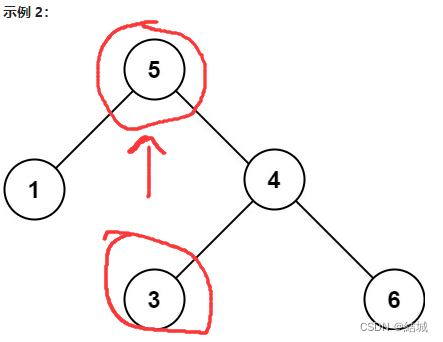
所以其实应该明白中序遍历是一个左中右的顺序,对应到二叉搜索树,自然就是一个升序序列了,所以写了这个
class Solution {
Deque<Integer> queue = new ArrayDeque<Integer>();
public boolean isValidBST(TreeNode root) {
dfs(root);
int v = queue.pollFirst();
System.out.println(v);
while (! queue.isEmpty()) {
int f = queue.pollFirst();
if (v >= f) {return false;}
v = f;
}
return true;
}
public void dfs(TreeNode root) {
if (root == null) {return;}
dfs(root.left);
queue.offerLast(root.val);
dfs(root.right);
}
}
但是这个队列的操作会拖慢运行时间,于是修改后如下
代码
class Solution {
TreeNode pre;
public boolean isValidBST(TreeNode root) {
if (root == null) {return true;}
boolean left = isValidBST(root.left);
if (pre != null && pre.val >= root.val) {return false;}
pre = root;
boolean right = isValidBST(root.right);
return left && right;
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 由Hello World的世界看世界
- Qt之QPainter绘制浪漫星空(快来许愿吧)
- 系统(嘀嗒)定时器
- [C#]使用PaddleInference图片旋转四种角度检测
- ClickHouse 入门与实战教程
- java经典程序
- 捍卫中华数学产权系列6.Σ1/n的分级通式与对应的求和公式
- 3Dmax模型打开后灯光全没了---模大狮模型网
- kubernetes(k8s)部署metrics及hpa-example示例
- Vue3 中 ref和reactive的区别是什么?