概率中的 50 个具有挑战性的问题 [9/50]：掷骰子

????????我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克·莫斯特勒（Frederick Mosteller）的《概率论中的五十个具有挑战性的问题与解决方案》）一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇文章只有 1 个问题，使其成为一个总共有 50 个部分的系列。让我们潜入并激活我们的脑细胞。

图片由作者使用 DALL-E 3 提供。

二、问题描述

????????掷骰子游戏，用两个骰子玩，是美国最快和最受欢迎的赌博游戏之一。计算与之相关的赔率是一项有启发性的练习。

????????规则如下：

1. 只有两个骰子的总数才算数。
2. 如果第一次掷骰子的总数为 7 或 11，则玩家掷骰子并立即获胜，如果掷骰子的总数为 2、3 或 12，则立即输掉。
3. 任何其他投掷都被称为他的“赛点”，即打平，继续对决。
4. 如果第一次掷骰子是一个点，玩家反复掷骰子，直到他要么再次掷骰子获胜，要么掷出 7 点输掉。

????????问：玩家获胜的机会有多大？

三、问题分析

3.1 概率空间分析

????????首先，让我们检查两次掷骰子产生的总计数的出现频率。

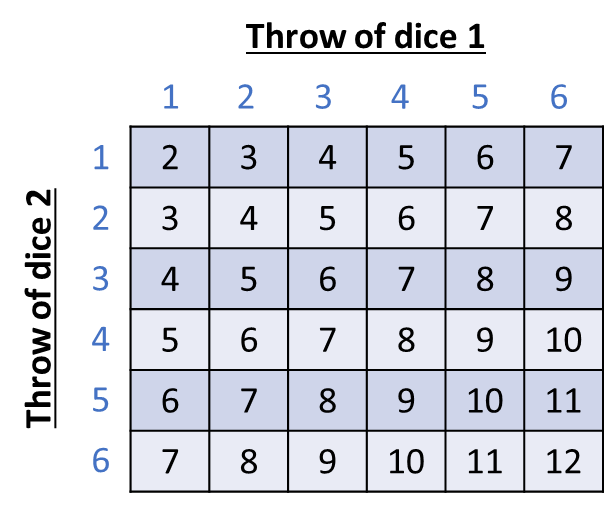
两个骰子计数的总数

???????

? 3.2??第一次投掷获胜的概率

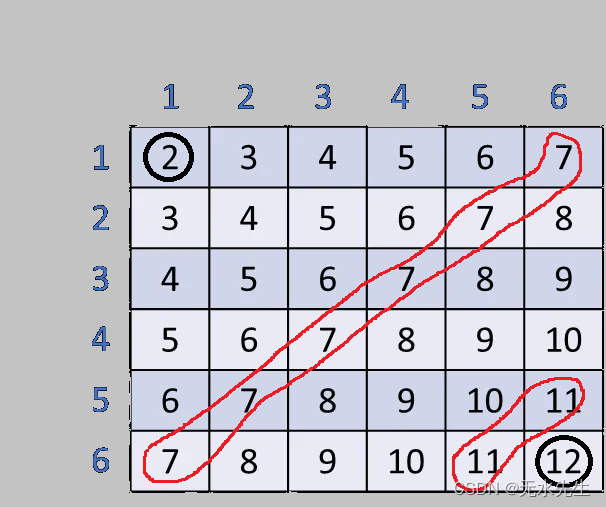
????????若首次投出骰子获胜，必须是。?为了确保在第一次投掷中取得胜利，玩家必须总共掷出 7 或 11 个。第一次投掷获胜的概率可以计算如下：

• 共 6^2=36?不同结果

• 投出 7的结果是:

  1. (1, 6)
  2. (2, 5)
  3. (3, 4)
  4. (4, 3)
  5. (5, 2)
  6. (6, 1)

• 投出11 的结果是:

  1. (5, 6)
  2. (6, 5)

• 因而产生出 8种不同的骰子结果使得首投获胜。

• Therefore, the probability of winning the first roll is equal to:

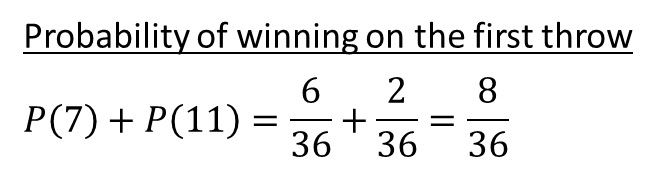
3.3 第一次投出获败概率

• 失去第一卷

掷 2 的方法有：

(1,1)

• 掷 3 的方法有：

(1, 2)
(2, 1)

• 掷出 12 的方法有：

(6, 6)
????????因此，有 4 种不同的掷骰方式会导致玩家在第一次掷骰时失败

????????因此，输掉第一卷的概率等于：

3.4 在投出赛点后获胜

????????如果玩家在第一次投掷时没有获胜，他们仍然可以通过在总共掷出 7 分之前再次掷出点来确保胜利。我们可以采用减少样本空间的方法来计算该概率，如下图所示。例如，在掷出总共 7 个之前再次掷出总共 4 个的概率可以通过将第一次掷出总共 4 个的概率乘以在掷出总共 7 个之前再次掷出总共 4 个的概率来计算。

????????通过将所有概率相加得到总获胜概率，如下图所示：

????????总获胜概率

总之，玩家的获胜几率为49.3%。

四、Python 代码?????????

import numpy as np

n_simulations = 100000
wins = 0
for _ in range(n_simulations):
    first_roll = np.random.randint(1, 7, size=2).sum()
    if first_roll in [7, 11]:
        wins += 1
    elif first_roll in [2, 3, 12]:
        continue
    else:
        while True:
            next_roll = np.random.randint(1, 7, size=2).sum()
            if next_roll == 7:
                break
            elif next_roll == first_roll:
                wins += 1
                break

probability_of_winning = wins / n_simulations
print(f'Probability of winning : {probability_of_winning:.3f}')

# Output:
# Probability of winning : 0.494

????????这就是这个垃圾游戏🎲问题的全部内容。欢迎任何反馈或问题！该代码可在我的?Github?上找到。请继续关注本系列的下一部分！:)