Datawhale 12月组队学习 leetcode基础 day3 递归
这是一个新的专栏,主要是一些算法的基础,对想要刷leedcode的同学会有一定的帮助,如果在算法学习中遇到了问题,也可以直接评论或者私信博主,一定倾囊相助
进入正题,今天咱们要说的是递归,递归是是很多初学者比较头疼的问题啊,在这篇博客里,我会先阐述一下递归的定义,然后再举几个例子来证明一下,最后咱们练个小题强化一下。
递归算法简介
首先说一下递归的含义,递归的含义就是,递归算法(recursion algorithm)在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。这是百度百科的定义 ,按照我们平时对递归的用法,那就是把一个大的问题一直分解,直到分解成一种简单的情况为止,这种简单的情况就是我们能直接得到结果的情况。下面先举一个例子,我们以阶乘为例,我们平时算阶乘是怎么算呢? 1的阶乘就是1, 2的阶乘就是 2*1 ,3的阶乘就是 3 * 2 *1 ,其实这里就是一个简单的递归 我们求3的阶乘的时候,要知道2的阶乘,用 3×2的阶乘,那么这里2的阶乘是哪里来的呢 是用2×1的阶乘 1的阶乘是哪里来的?是规定 1的阶乘就是1.所以我们才能算出来3的阶乘。那么在计算机的语言里,我们一般是用函数调用自己的方式来实现递归,举个例子:
int func(int n)
{
if (n == 1)
return 1;
else return n * func(n-1);
}
这个就是使用C++语言写一个简单的递归来解决阶乘问题的方法,我们简单分析一下,这个函数为什么能算阶乘?
当n等于1的时候 就返回1,如果n = 2呢?就调用else中的return 返回 n*func(n-1),即为 2×func’(1)也就是1的阶乘 1的阶乘用函数算出来就是1 这里就是2×1 其实这样还不够直观,因为递归的过程分为递推和回归两个过程,这里画个图让大家好理解一下:
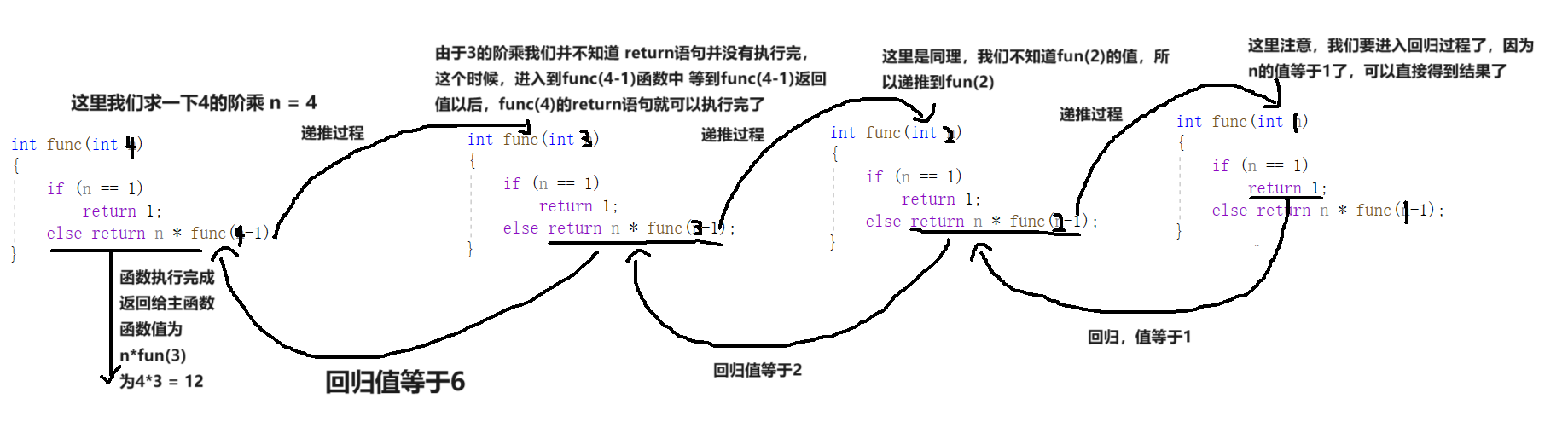
递归算法解题思路
现在我们可以总结一下了,递归在计算机语言中解决问题的步骤是什么?
递推过程:指的是将原问题一层一层地分解为与原问题形式相同、规模更小的子问题,直到达到结束条件时停止,此时返回最底层子问题的解。
回归过程:指的是从最底层子问题的解开始,逆向逐一回归,最终达到递推开始时的原问题,返回原问题的解。
遇到问题时 我们只需要想好其中一个递推的过程和一个回归过程即可,不用全都想透,这样容易乱掉,其实这也是一个重复的过程,套路都是一样的
例题
下面我们练一个递归算法的经典小题
例题1

先说一下斐波那契数列是啥 他是 第0项为0 第1项为1(规定),从第三项开始 每一项都是前两项的和 这么一个数列 比如f(2) = f(0)+f(1)
这时候我们就想一下他的递推过程是啥,回归过程是啥,递归过程就是:比如我们要求 f (6) 的值 f,那么就要知道 f(4)和f(5)的值,f (4) 又要知道f (3) 和f(2)的值,一次类推 知道递推到 f(0)和f(1)的值 我们就可以return了,这里建议大家画图,不清晰一定画个图。
那么代码如何写呢?

可以看到,这里时间耗时比较长哈,这是因为在求斐波那契数列的时候有重复,就像我们求f(6),要求f(5)和f(4) f(5)要求f(4)和f(3),这里两个f(4)就重复了,这时我们可以使用记忆化的方式去简化,具体就是算完一个f 就存在数组里一个值,下次遇到已经存进去的值,就可以直接调用了,这里不提供代码,大家可以回去查阅一下。
练习
二叉树最大深度
这里没有学过二叉树的可以去看我的另一篇博客,可以简单了解一下,二叉树简单介绍
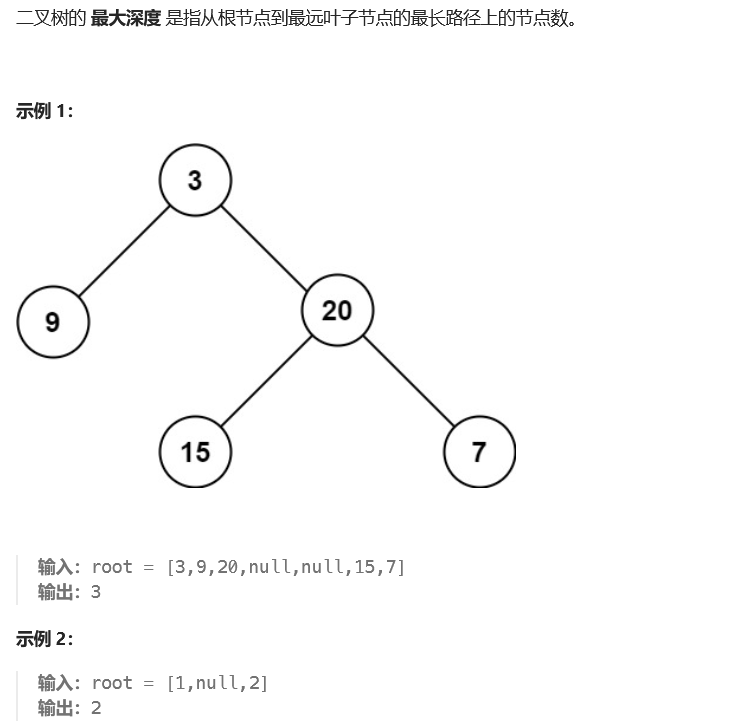
这里简单给个思路 就是二叉树有左子树和右子树 其中更深的就是我们要的答案
代码如下:做完再看嗷
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == nullptr)
return 0;
int hleft = 0;
int hright = 0;
hleft = maxDepth(root->left);
hright = maxDepth(root->right);
return hleft > hright? hleft+1: hright+1;
}
};
有啥问题都可以提出来 ,博主有啥问题也恳请斧正,谢谢。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- MYSQL的锁
- 【Java万花筒】云端之旅:Java容器化、微服务与云服务之道
- 基本算法(货仓选址)-排序【竞赛题】
- 2023数据库编程大赛-答辩总结
- 风二西CTF流量题大集合-刷题笔记|基础题(4)
- 进阶Docker4:网桥模式、主机模式与自定义网络
- 【Mode Management】CanSM详细介绍
- 服务器数据恢复—raid5热备盘未激活崩溃导致上层oracle数据丢失的数据恢复案例
- lv14 并发控制:上下文、中断屏蔽和原子变量
- Office提示内存或磁盘空间不足