运动的解析:从机械运动到自由落体,探索物体运动的基本规律与数学描述
文章目录
- 一、机械运动
- (一)运动概念
- (二)运动形式
- (三)参照物
- 二、质点
- (一)理想化模型
- (二)质点概念
- 三、位移和路程
- (一)位移
- (二)路程
- (三)位移和路程的关系
- 四、速度和速率
- (一)速度
- 1、平均速度
- 2、瞬时速度
- (二)速率
- 1、平均速率
- 2、瞬时速率
- 五、加速度
- (一)加速度概念
- (二)加速度定义
- (三)加速度方向
- (四)速度与加速度的关系
- 六、匀速直线运动
- (一)定义
- (二)特点
- (三)公式
- 1、位移公式
- 2、速度公式
- 七、匀变速直线运动
- (一)定义
- (二)特点
- (三)公式
- 1、速度公式
- 2、位移公式
- 3、速度位移公式
- 4、平均速度公式
- 八、匀变速直线运动的推论
- 推论1、 v ˉ = v t 2 = v 0 + v t 2 \displaystyle \bar v=v_\frac{t}{2}=\frac{v_0+v_t}{2} vˉ=v2t??=2v0?+vt??
- 推论2、 v s 2 = v 0 2 + v t 2 2 \displaystyle v_\frac{s}{2}=\sqrt{\frac{v_0^2+v_t^2}{2}} v2s??=2v02?+vt2???
- 推论3、 Δ s = s n + 1 ? s n = a t 2 = 恒 量 \Delta s=s_{n+1}-s_n=at^2=恒量 Δs=sn+1??sn?=at2=恒量
- 九、自由落体运动
- (一)条件
- (二)性质
- (三)公式
- 1、速度公式
- 2、位移公式
- 3、速度位移公式
- 十、运动图像
- (一)位移图像(s-t图像)
- (二)速度图像(v-t图像)
- 十一、案例演示
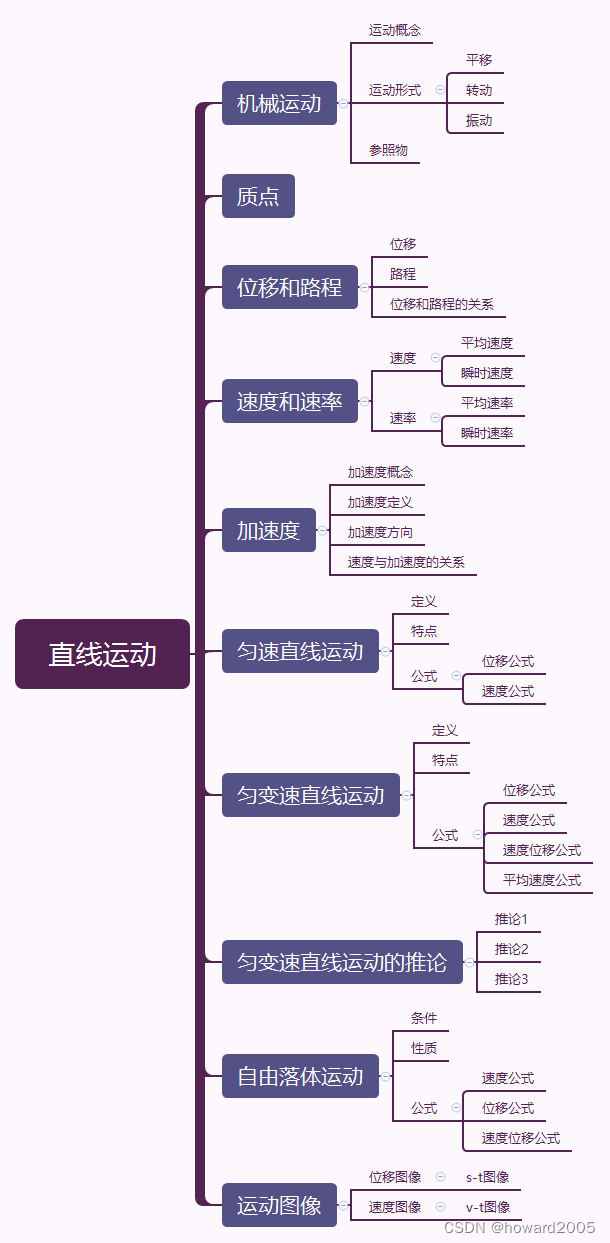
在物理学浩瀚的宇宙中,探索运动奥秘是一场引人入胜的旅程。从日常生活的点滴到宇宙万物的运转,机械运动以其多样性和规律性编织了世界的动态画卷。一元二次方程作为数学语言,帮助我们精确刻画和预测物体的位置变化;质点概念则是简化复杂现实、洞察力与质量相互作用的关键一步。位移与路程描绘出轨迹的曲折与直线,速度与加速度揭示着运动状态的瞬息万变。自由落体运动则展示了重力法则对万物的普适影响。而通过位移图像与速度图像,我们将抽象的运动过程可视化,使深藏于时间和空间中的物理信息跃然纸上。接下来,我们将一起深入剖析这些基本概念,以实例演示的方式,生动形象地解读运动背后的数学规律,从而揭开自然界奇妙无比的运动面纱。
一、机械运动
(一)运动概念
- 在奇妙的物理世界中,想象一下你正在观察一颗行星绕着恒星旋转、一片树叶随风摇曳或是小球沿斜面滚动的情景。这些生动活泼的现象揭示了运动的基本概念:机械运动(mechanical motion)是指一个物体相对于另一个参考物的位置发生变化的过程。就像一位舞者在舞台上翩翩起舞,其位置随时间和空间不断演变,这种动态变换就是我们所说的“运动”,它是宇宙万物生机盎然、生生不息的直观体现,是自然界最基础也最为壮丽的表演之一。
(二)运动形式
- 机械运动的多彩世界中,蕴含着丰富多样的动态形态。想象一下,平动(translation) 仿佛是一位舞者在舞台上沿直线优雅滑行,无论是在广阔的平原还是无限延伸的轨道上,都展现着匀速或变速的直线之美;转动(rotation) 则如同芭蕾舞者轻盈地旋转,从微观世界的原子电子到宏观世界的地球自转,无不体现出旋转带来的周期韵律和动力平衡;而振动(vibration) 就像是琴弦上的音符跃动,既有弹簧振子在静止与极限位置间的往复跳跃,也有声波在空气中的传播波动,揭示了自然界和谐而又充满活力的一面。这些平动、转动和振动共同构成了机械运动的基础元素,生动展现了物体运动形式的千变万化。
(三)参照物
- 在研究物体运动这一奇妙的探索之旅中,参照物(reference object) 扮演着至关重要的角色。想象一下自己坐在一艘飞驰的列车上,手中的苹果看似静止不动,但如果以窗外疾驰而过的站台为参照,则会发现苹果其实正在“飞翔”。为了准确捕捉和描绘物体运动的真实面貌,科学家们精心挑选一个假定静止不动的参照物作为观察坐标系的核心。通常情况下,我们选择坚实的地球作为参照基石,以此为基础来剖析万物运行轨迹与速度变化。然而,在浩瀚宇宙间,任何物体都可以成为参照物,选择的不同将演绎出多维度、多视角下千变万化的运动故事,让物理学的世界充满了生动与趣味。
二、质点
(一)理想化模型
- 理想化模型,这可是物理学家手中的魔法棒!想象一下,你正在跟一个无比复杂的“实物先生”打交道,他身上各种属性琳琅满目,像是缠绕着无数条线索的角色。他的体积、形状、质量,甚至那些隐藏在微观世界里的小秘密,都像是一部未解之谜的大戏。但是,我们的物理大侦探为了揭示宇宙的简单法则,施展了一招“理想简化大法”。他们大胆地将这位“实物先生”剥离到只剩最核心的特征,把那些无关紧要的琐碎细节一股脑儿塞进看不见的魔法口袋里。瞧,这样一来,“理想模型先生”就闪亮登场了——简洁明快,恰似一位只保留最关键剧情线的幽默角色,让科学研究变得轻松愉快又富有成效。
(二)质点概念
-
在物理学的奇幻世界里,质点(mass point,particle) 就如同一个隐身术大师,它是个有质量却无体积、无形状的“神秘小精灵”。想象一下,你正在和一位身形庞大、结构复杂的怪兽打交道,而为了搞清楚它的运动规律,你灵机一动,施展了一招“化繁为简”的魔法。于是乎,这位庞然大物瞬间变成一个只有质量的神奇点状存在,我们亲切地称之为“质点”。
-
力学研究时,就好比是给这个宇宙大舞台上的演员们量身定制戏服,只需关注他们在引力作用下的舞步轻重(即质量),至于他们穿的是华丽长袍还是朴素布衣(即体积和形状),对这场宏观舞蹈的影响微乎其微,完全可以忽略不计。
-
所以,无论是微观世界的微小电子、质子、中子这些小个头角色,还是地球上的生物、物体,甚至是宇宙中的恒星、行星等天体巨星,只要它们的运动问题简化到只关心位置变化,并且所考察的空间范围远大于它们自身的大小,都可以被我们魔法师般的物理学家施以“质点化”咒语,将它们统统变身为质点,以便于我们在力学的剧本中轻松解读它们的精彩表演!
三、位移和路程
(一)位移
- 想象一下,你是一位侦探,在追踪一只敏捷狡猾的猫在房间内的运动轨迹。位移displacement) 就像是你在地图上从猫最初蜷缩的小窝(初位置)到它最后跃上的窗台(末位置)画出的一条指向性小箭头,这条神秘的“矢量线段”记录了猫在空间中乾坤大挪移的秘密路径。可不是嘛,位移这家伙就是物理学里那位专门讲述物体如何从“A点瞬移到B点”的幽默故事家,只不过它用的是严谨而生动的几何语言,让你瞬间get到物体位置变化的关键情节!
(二)路程
- 路程(distance travelled),这个家伙就像一位乐此不疲的旅行家,它忠实记录着物体在运动过程中的“游记”长度。想象一下,你的小车轮胎是个热爱探险的勇士,每滚动一寸,都在地图上留下一道印记。这一路走过弯弯曲曲、高低起伏,累积起来的总里程数就是它的“游历战绩”,而这路程啊,可不管你是直行、拐弯还是上下坡,总之,只要是实实在在走过的每一步,都会被这位一丝不苟的统计员一笔一划地记下来。只不过呢,它只关心走了多远,而不在意方向,所以呀,它可是个只会报数、不会指路的“标量”型向导。
(三)位移和路程的关系
-
想象一下,位移和路程这对冤家就像是两位风格迥异的旅行者。位移老弟是个直来直去、一针见血的家伙,只关心从起点到终点最直接的距离;而路程兄可就复杂多了,他喜欢沿途欣赏风景,绕弯路对他来说是常事,所以走过的总长度自然更长。
-
在现实生活中,除非你像快递员送直线距离最近的包裹那样,从A点径直跑到B点(即单方向直线运动),这时位移大小才与路程相吻合。其他时候嘛,位移老弟总是抱怨路程兄太能绕圈子,毕竟人家只算两点间的直线距离,而路程兄可是把每一步都算得明明白白。
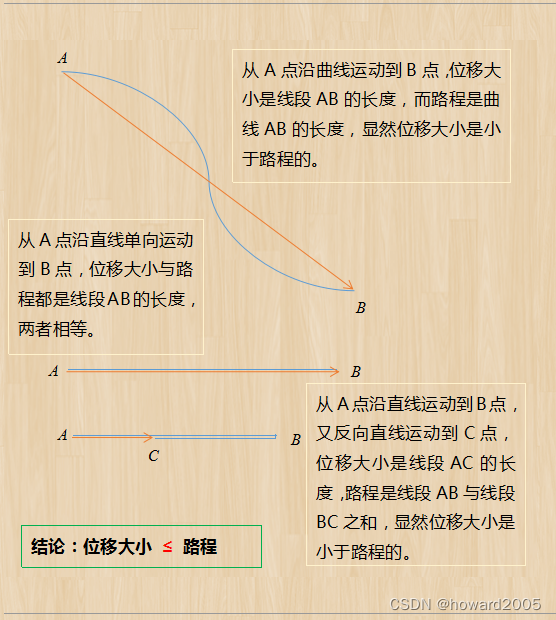
位移路程本不同,
区分两者自从容。
倘若只需论大小,
路程较长理才通。
四、速度和速率
(一)速度
- 速度(velocity),这个物理界的“快慢侦探”,可不只是单纯告诉你物体是急如闪电还是慢如树懒那么简单。它更像是一位自带方向感的超级英雄,不仅揭示了物体运动的速度大小,还挥舞着矢量这把神奇罗盘剑,指引着物体行进的方向。所以啊,下次当你抱怨自己跑得不够快时,不妨先问问这位矢量侦探:“我这是朝着正确的方向全力以赴了吗?”
1、平均速度
- 了解概念:平均速度(average velocity),这位憨厚的物理界“老司机”,可不像我们想象中的那么普通。它就像一位热心肠的大叔,帮你计算从起点到终点的“全程驾驶”平均时速。不论你的车速如何上蹿下跳,大叔都会笑眯眯地告诉你:“别管中间那些加速刹车的小插曲,我给你算的是这一趟行程总的‘悠哉悠哉’平均快慢。”所以,当你想知道某段变速运动旅程的大概有多快时,找这位“平均速度大叔”准没错!
- 计算公式: v avg = Δ x Δ t = x 2 ? x 1 t 2 ? t 1 \displaystyle v_{\text{avg}}=\frac{\Delta x}{\Delta t}=\frac{x_2-x_1}{t_2-t_1} vavg?=ΔtΔx?=t2??t1?x2??x1??,这个公式就好比是速度世界的“烹饪秘诀”:想象你是一位在时空厨房里的大厨,要测量物体从位置 x 1 x_1 x1?移动到位置 x 2 x_2 x2?的平均速度。 Δ x \Delta x Δx就像是食材中的“距离馅饼”,而 Δ t \Delta t Δt则是掌控火候的关键——“时间调料”。大厨只需将馅饼(位移差)均匀切成小块,再用调料(时间间隔)调味,最终得到的就是美味可口的平均速度菜肴 v avg v_{\text{avg}} vavg?。换句话说,就是把物体经过的总路程除以花费的总时间,就能得出它在整个过程中悠闲漫步或疾驰狂奔的平均速度啦!
2、瞬时速度
- 了解概念:瞬时速度(instantaneous velocity),这位物理界的“超能力侦探”,有着捕捉瞬间动态的神奇本领。想象你正在追踪一个不断变速的魔术师,普通的平均速度只能告诉你他大概有多快,而瞬时速度则能精准揭露他在某一眨眼间的惊人速度和方向——就像在高速旋转的摩天轮上,某一片刻指向天空的那个速度箭头。所以,瞬时速度就是在物体运动轨迹上演绎“速度芭蕾”的关键舞者,它的舞步沿着切线翩翩起舞,将变速运动最细腻、最真实的那一刹那展现得淋漓尽致!
- 计算公式: v = lim ? Δ x → 0 Δ x Δ t = d x d t \displaystyle v=\lim_{\Delta x \to 0}\frac{\Delta x}{\Delta t}=\frac{dx}{dt} v=Δx→0lim?ΔtΔx?=dtdx?,这个公式就像是速度家族的“魔法咒语”,用来揭秘瞬时速度这位隐身的高速精灵。想象你是一位物理学世界的哈利·波特,想要找出物体在某一精确时刻(比如它正从一个飞贼手中巧妙地接过金色飞贼)的速度秘密。首先,我们使用 Δ x \Delta x Δx和 Δ t \Delta t Δt这对“时间空间双胞胎”,分别代表物体在微小距离内的位移变化和对应的时间间隔。随着我们的“魔法棒”挥舞,让这个距离趋近于零( Δ x → 0 \Delta x \to 0 Δx→0),就仿佛用高倍显微镜聚焦到那转瞬即逝的一刹那。然后,神奇的事情发生了,这个极限过程揭示了物体在那一瞬间的真实速度,也就是瞬时速度 v v v。而通过微积分的魔力,我们将这一过程转化为对位置函数 x ( t ) x(t) x(t)求导数 d x d t \displaystyle\frac{dx}{dt} dtdx?,这就像是给运动轨迹施加了一个时空加速魔法,使得原本模糊的速度变得清晰可辨,犹如变魔术般精准无误!
(二)速率
- 速率(speed),这位物理界的“速度直男”,只关注运动的快慢程度,对方向可是不屑一顾。它就像个只看速度表、不管车辆朝哪开的司机大哥:“嘿,甭管你往东还是往西,我只关心油门踩下去能跑多快!”所以,速率就是一个单纯的数字游戏,无论你是在赛道上疾驰,还是在原地打转,只要速度快,那这个标量老兄就会给你点个大大的赞!
1、平均速率
-
了解概念:平均速率(average speed) 这位物理世界的“公路巡警”,可不管你是在直道上疾驰,还是在弯道上绕圈。它只关心一件事:你在规定的时间内究竟走了多远的路。想象一下,你正在驾驶一辆车,无论你是直线狂飙,还是曲折蛇行,只要算一算这段时间走过多少里程除以所用时间,就是这位巡警开出的“平均速度罚单”啦!所以,甭管道路多么崎岖蜿蜒,平均速率都会实事求是地告诉你:“小子,你的平均‘脚程’是多少!”
-
计算公式: s avg = total?distance Δ t \displaystyle s_{\text{avg}}=\frac{\text{total}\ \text{distance}}{\Delta t} savg?=Δttotal?distance?,这个公式就像一场有趣的旅行挑战:假设你是一位探险家,手中握有一张神秘地图,上面标示着一段旅程的总距离(total distance)。而 Δ t \Delta t Δt则代表了你完成这段旅程所花费的全部时间。于是乎,平均速率这位“旅行导师”就出现了,他告诉你:“小子,想知道你这一路平均下来每分钟(或每小时)走了多远吗?很简单,只要把全程总距离除以你耗掉的时间,就能得到你的平均速度勋章—— s avg s_{\text{avg}} savg?!”换句话说,无论你是翻山越岭还是穿越沙漠,只需用走过的所有里程除以消耗的所有时间,就可以算出你在整个探险过程中的平均步速啦,是不是挺像一场充满乐趣与挑战的竞赛游戏呢?
-
平均速度与平均速率的关系:想象一下你正在参加一场疯狂的障碍越野赛,赛道上有直道也有曲折的弯道。平均速度就像是你的“理想直线驾驶速度”,它只计算你在各个方向上位移的大小与时间的比值,对于那些反复折返和绕圈的部分,并不会增加位移。而平均速率则是那个手持秒表、一脸严肃的裁判,他不管你开的是直是弯,只关心你实际在赛道上行驶过的总路程与所用时间的比例。所以,在这场混乱复杂的比赛中,你的平均速度可能因为不断改变的方向而小于实际走过的平均速率。只有当你在完全笔直无弯道的赛道上驰骋时(即单方向直线运动),理想直线驾驶速度和实际经过的路程才会完美匹配,这时候平均速度和平均速率才真正握手言和,达成一致: ∣ v a v g ∣ ≤ s a v g |v_{avg}|\le s_{avg} ∣vavg?∣≤savg?。
2、瞬时速率
-
瞬时速率(instantaneous speed) 这位急性子的物理小哥,可不愿意等到比赛结束才告诉你速度。它就像一位拿着超级放大镜、对准赛车仪表盘的疯狂粉丝,专门捕捉赛车在每一个瞬间、每一个心跳时刻的速度值。
-
想象一下,你正驾驶着一辆F1赛车,瞬时速率就是那个每分每秒都盯着你速度表的“速度侦探”,无论你是在直线加速还是弯道漂移,它都能立刻告诉你此刻轮胎与地面摩擦产生的火花到底有多快。所以,瞬时速度和瞬时速率其实就是一对孪生兄弟,一个关注速度的方向(矢量),一个只在乎速度的大小(标量),而在瞬时这个点上,它们俩的意见一致了——瞬时速度的大小就是瞬时速率!
五、加速度
(一)加速度概念
- 加速度(acceleration),这位物理世界的“速度魔术师”,它的拿手好戏就是施展“快慢变化”的神奇魔法。想象一下你驾驶一辆超级跑车,当你猛踩油门时,它就犹如一位严厉的教练在背后推你一把,让你的速度噌噌噌地往上窜;反之,当你急踩刹车时,它又像是一股无形的力量拽着你减速,这就是加速度在捣鬼。简单来说,加速度就像个急性子的导演,专门负责指挥速度如何快速、精准地切换场景,而方向则是它挥舞的指挥棒,让物体在三维空间中或加速前进、或急转直下,玩转速度的变化率游戏!
(二)加速度定义
-
加速度,这位物理界的“速度教练”,可不仅仅满足于知道物体跑得有多快。在匀变速直线运动的训练场里,它更关心速度提升的效率——想象一下,你正在驾驶一辆性能卓越的赛车,从起步到瞬间飞驰,加速度就是那个帮你计算“从零飚到一百所需时间”的严厉教官。
-
具体来说,如果赛车在一段时间 Δ t Δt Δt内,速度由 v 1 v_1 v1?飙升至 v 2 v_2 v2?,这位严格的教练就会用公式 a = Δ v Δ t = v 2 ? v 1 t 2 ? t 1 \displaystyle a=\frac{\Delta v}{\Delta t}=\frac{v_2-v_1}{t_2-t_1} a=ΔtΔv?=t2??t1?v2??v1??来评估你的“提速表现”。而在复杂多变的一般变速运动中,这个公式给出的就是平均加速度,相当于你在整个加速过程中的“综合成绩”哦!
(三)加速度方向
-
加速度这位物理界的“导航员”,虽然它总是指向速度变化的方向,但可不是每次都会和当前行驶方向保持一致。想象一下你正在一艘宇宙飞船上驾驶,突然来了个急转弯,飞船的速度瞬间从向前变成了向左,这时加速度就像是那位果断指挥转向的船长,毫不犹豫地指向了速度变化的方向——左边。
-
所以,当你的速度由 v v v改变到 v + Δ v v+Δv v+Δv时,无论这个变化是增速还是减速,亦或是改变方向,加速度这家伙都会坚定不移地指向速度增量 Δ v Δv Δv的方向,就像一个忠诚却又不按常理出牌的副驾驶,时刻准备引领你进入下一个未知的飞行阶段。
(四)速度与加速度的关系
-
加速度这位物理世界的“急性子”,它与速度大小并无直接交情,而是死磕速度的变化。想象一下你是一位赛车手,无论你的车速是风驰电掣还是慢如蜗牛,只要油门在变(速度变化),这位急性子教练就会在一旁激动地计算你的“反应能力”——也就是加速度。
-
所以,只要速度不改变(匀速行驶),即使你是赛道上的闪电侠,急性子教练也会悠闲地打个盹儿,因为此时加速度为零。反之,只要你踩油门或刹车的动作够猛(速度变化快),哪怕此刻车速并不大,急性子教练也绝对会瞪大眼睛,因为它知道,此刻你的加速度表现正在蹭蹭上涨!
六、匀速直线运动
(一)定义
- 想象一下,你正在跟一只超精准的机械蜗牛赛跑,这只蜗牛每秒钟都能挪动相同长度的距离,从不偷懒也从不懈怠。这就是匀速直线运动(uniform rectlinear motion)——无论时间老人如何催促或拖延,它都保持着那份“稳如老狗”的步伐,在直线上优雅地滑行,每一秒、每一刻的位移都是复制粘贴般的一致。所以呢,这种“蜗牛式”跑步法在物理世界里有个高大上的名字:匀速直线运动!
(二)特点
- a = 0 , v = 恒 量 a = 0,v = 恒量 a=0,v=恒量(大小恒定、方向不变)
- 匀速直线运动这位“淡定哥”,它最大的特点就是始终保持着佛系的心态和稳定的步伐。想象一下,你驾驶着一辆配备魔法引擎的汽车,无论上坡、下坡还是平地,油门一旦固定,车速就雷打不动( v = v= v=恒量),连拐弯都懒得拐,只爱笔直前行。而且呀,这辆车还自带“零加速”特效,不管你多用力踩油门或刹车,加速度 a a a始终保持为零。所以,匀速直线运动就像一位永不停歇的马拉松选手,既不加速也不减速,只保持一个永恒不变的速度,在同一条直线上悠哉游哉地奔跑!
(三)公式
1、位移公式
-
s = v t s=vt s=vt,这个公式就像是匀速直线运动这位“马拉松选手”的成绩单。在这个简单而又神奇的等式 s = v t s=vt s=vt中," s s s“代表了它跑过的总路程,而” v v v"则是它永恒不变的速度。想象一下,你手握一块可以自动保持速度的滑板,在一条直线上畅滑。每过一秒(或任何单位时间),滑板都会精确地移动 v v v米的距离。
-
所以,如果你想知道在 t t t时间内能滑多远,只需将速度乘以时间,就像把秒表上的时间数和每秒前进的距离相乘一样。这样,无论滑多久,只要速度恒定,你都可以用这个简单的公式轻松算出你的位移成绩啦!
2、速度公式
-
速度公式 v = s t \displaystyle v=\frac{s}{t} v=ts?就像是物理世界的“时空侦探”,专门追踪物体在直线上的运动故事。想象你是一位快递员,手中有一份包裹需要从起点(0米)送到终点(s米)。侦探就站在一旁掐着秒表,记录下你完成这段旅程所用的时间(t秒)。
-
于是乎,这位聪明的侦探只需简单除法,就可以揭示出你在整个过程中平均每秒钟前进多少距离,也就是你的平均速度v。所以说,甭管是疾驰的赛车还是悠闲散步的大象,只要你告诉侦探空间位移和时间,它就能帮你算出那个神秘的速度值!
七、匀变速直线运动
(一)定义
- 想象一下你驾驶一辆拥有神奇自动档位的赛车,在直线上行驶时,无论何时踩下油门或刹车,它都能保证每秒钟速度变化量完全一样。这就是匀变速直线运动(rectlinear motion with constant acceleration)——一个在速度上“任性”且“专一”的家伙,不论时间老人怎么催促或是拖延,它都坚持着每一秒加/减相同的速度值,如同一位对速度变化有着强迫症的司机,沿着笔直的道路以恒定的加速度尽情驰骋!
(二)特点
- a = 恒 量 a = 恒量 a=恒量 (大小恒定、方向不变)
- 匀变速直线运动这位“毅力哥”,它的拿手好戏就是在直线上玩持久不变的加速游戏。想象一下,你正在驾驶一辆装有神秘恒定动力装置的跑车,在广阔的公路上疾驰。不论过了多久,这辆车的加速度 a a a就像个顽固的孩子,坚持着大小不变、方向不改的原则,一路向前冲。
- 换句话说,无论是在起跑阶段还是冲刺时刻,只要你踩下油门那一刻确定了加速度,它就仿佛被施了魔法一般,始终保持着那个恒定值,让你在直道上体验一段既稳定又刺激的加速旅程!
(三)公式
1、速度公式
-
速度公式 v = v 0 + a t v=v_0+at v=v0?+at就像是你在物理世界的“速度魔法棒”。想象一下,你正在驾驭一辆带有神秘引擎的飞车,初始速度是 v 0 v_0 v0?(就像刚从车库启动时的速度),而 a a a则是你的神奇加速度。
-
这个公式就好比是一个实时速度升级器:在任意时刻 t t t,只要挥动“速度魔法棒”,当前速度就会自动加上这段时间内积累的加速度效应。换句话说,无论你现在开多快( v 0 v_0 v0?),只要保持恒定的加速度 a a a持续施法,每一秒后,你的速度都会像坐火箭般噌噌上涨,直至变成 v 0 + a t v_0+at v0?+at!
2、位移公式
-
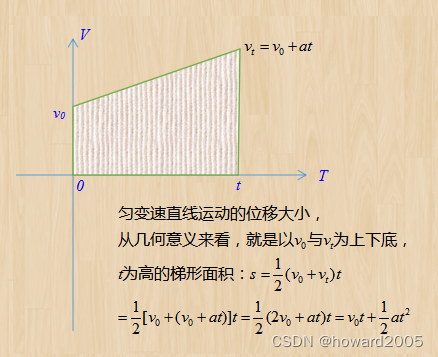
位移公式 s = v 0 t + 1 2 a t 2 \displaystyle s=v_0t+\frac{1}{2}at^2 s=v0?t+21?at2就像是物理学中的“时空计算器”,它帮你预测在匀变速直线运动中,物体从起点出发后会在什么位置留下它的足迹。想象一下你正在驾驶一辆拥有神奇加速度的飞车。
-
初始时刻,你的车速是 v 0 v_0 v0?,就好比你在起跑线上蓄势待发;而 a a a则是你的超能力加速度,始终如一地推动着汽车前进。随着时间 t t t的推移,车子不仅会按照初始速度行驶一段距离( v 0 t v_0t v0?t),还会因为加速度的作用,在这段时间内额外获得一个由加速度和时间平方( 1 2 a t 2 \displaystyle \frac{1}{2}at^2 21?at2)共同构建的神秘位移奖励。所以,甭管过了多久,这个公式都能精确告诉你,你的小飞车将稳稳地停在哪个坐标点上!
3、速度位移公式
-
速度位移公式 v t 2 ? v 0 2 = 2 a s v_t^2-v_0^2=2as vt2??v02?=2as就像是物理学的“速度与距离的秘密协议”。想象一下,你驾驶着一辆拥有神秘加速度的赛车,在一场奇幻的直线竞速中,从初始速度 v 0 v_0 v0?开始加速。
-
这个神奇的公式揭示了一个秘密:在任意时刻 t t t,你的赛车最终速度 v t v_t vt?与起始速度 v 0 v_0 v0?之间速度差的平方,等于整个过程中加速度 a a a和行驶过的位移 s s s两倍相乘。也就是说,无论你的赛车如何加速冲刺,只要你知道了起点、终点的速度以及全程加速度,就能通过这个公式揭开这场速度与距离之间的激情碰撞!

4、平均速度公式
-
平均速度公式 v avg = v 0 + v t 2 \displaystyle v_{\text{avg}}=\frac{v_0+v_t}{2} vavg?=2v0?+vt??,就像是赛车手在匀变速直线赛道上的“折中裁判”。想象一下你是一位拥有神秘加速度的飞车驾驶员,在一场决定性的直线加速赛中,你的车从初始速度 v 0 v_0 v0?起步,经过一番激烈的加速后最终达到了速度 v t v_t vt?。
-
这个有趣的公式就像是裁判手中的魔法尺子,它不关心你在比赛过程中如何风驰电掣、如何超越极限,只用一个简单的算术平均法,将你的起始速度和结束速度一分为二,告诉你在这段疯狂旅程中,如果忽略那些曲折变化,你的赛车保持着怎样的平均速度疾驰而过。
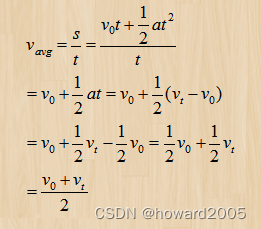
-
以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“
+”值,跟正方向相反的取“-”值。
八、匀变速直线运动的推论
- 想象一下,匀变速直线运动就像是物理世界的“魔法方程式”,而那些推论就是藏在方程式背后的“小魔术”。掌握这些推论,就如同手握解开神秘时空锁链的钥匙。通过深入挖掘和灵活运用,我们能洞察到速度与位移之间的巧妙关联,宛如侦探破解复杂案件一般,在解决各类特殊运动问题时,轻挥魔杖,瞬间点亮思维的火花,让难题迎刃而解,也让物理学的学习之旅充满乐趣与挑战!
推论1、 v ˉ = v t 2 = v 0 + v t 2 \displaystyle \bar v=v_\frac{t}{2}=\frac{v_0+v_t}{2} vˉ=v2t??=2v0?+vt??
- 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,等于这段时间初末速度的平均值。
- 这个推论就像是一场匀变速直线运动的“速度魔法秀”。想象一下,你正在驾驶一辆拥有神秘加速度的跑车,在一场激动人心的直线加速赛中,从初始速度
v
0
v_0
v0?出发,一路疾驰至最终速度
v
t
v_t
vt?。而这场表演中的高潮部分就是:在行驶时间
t
t
t正中间的那个神秘时刻,你的跑车会瞬间展现出一个特别的速度——它恰好等于这段时间内平均速度和初末速度的“黄金分割点”,也就是它们两者相加除以2。换句话说,无论你的跑车在这段时间内如何疯狂加速,那个奇妙的中场时刻,它的即时速度就像是魔术师手中的魔杖轻轻一点,就神奇地变成了整个加速过程的一个完美缩影!
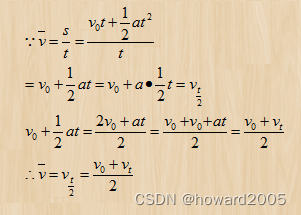
推论2、 v s 2 = v 0 2 + v t 2 2 \displaystyle v_\frac{s}{2}=\sqrt{\frac{v_0^2+v_t^2}{2}} v2s??=2v02?+vt2???
-
做匀变速直线运动的物体在一段位移的中点的即时速度等于初末速度平方和一半的算术平方根。
-
这个推论就像是匀变速直线运动中的“速度魔法公式”,它揭示了一个令人惊奇的秘密。想象一下,你正在驾驶一辆拥有神秘加速度的飞车,在一段直线上从初始速度 v 0 v_0 v0?加速到最终速度 v t v_t vt?。
-
在这个奇幻的过程中,有一个特别时刻发生在位移的一半位置,这时的速度就像被施展了魔法一样,恰好等于初末速度平方和除以2后的算术平方根,即 v s 2 = v 0 2 + v t 2 2 \displaystyle v_\frac{s}{2}=\sqrt{\frac{v_0^2+v_t^2}{2}} v2s??=2v02?+vt2???。
-
换言之,无论你的赛车如何在赛道上疾驰,当你驶过一半路程时,车辆瞬间展现出一个神奇的速度值,这是初速度和末速度两位魔法师共同施法的结果。这个有趣的规律不仅有助于我们更好地理解物体的运动状态,还能帮助我们在解决相关问题时找到一条捷径!

推论3、 Δ s = s n + 1 ? s n = a t 2 = 恒 量 \Delta s=s_{n+1}-s_n=at^2=恒量 Δs=sn+1??sn?=at2=恒量
-
匀变速直线运动的质点,在任意两个连续相等时间t内的位移差值是恒量。
-
这个推论就像匀变速直线运动的“时空等差序列”。想象你正在驾驶一辆拥有神秘恒定加速度的飞车,每次踩下油门,它都会在相等的时间间隔内增加一段确定的距离。
-
这个推论揭示了一个有趣的现象:无论你是在比赛开始时、中途还是即将冲线时踩下油门,只要时间间隔相同,汽车在这两个瞬间经过的位移增量( Δ s \Delta s Δs)总是一样的。这就像是每过一个固定时间,你的飞车就会自动向前跳跃一段固定的“时空步长”,而且这个步长 a × t 2 a \times t^2 a×t2是恒定不变的。所以,在这场奇幻的物理旅程中,你可以轻松预测任意两个连续相等时间段内的前进距离,是不是很像在玩一场穿越时空的跳格子游戏呢?

九、自由落体运动
- 想象一下,在遥远的17世纪,智慧如侦探般的托斯卡纳科学家伽利略正像破解悬案般揭示了大自然的秘密:力如何影响物体运动。这位物理界的“福尔摩斯”在1638年的大作中,首次揭秘了自由落体运动这一“自然剧场”的剧本公式。就如同他从比萨斜塔上扔下两个不同重量的苹果,结果它们同时落地一样令人拍案惊奇。原来,不考虑空气阻力时,所有物体下落的速度都遵循一个神秘而恒定的数学法则,就像舞台上的演员按照预定剧本整齐划一地表演高空跳水,每一幕都精准无误,让人不禁感叹科学世界的神奇魅力!
(一)条件
-
初速度为零,只受重力作用。
-
自由落体运动就像是物理世界的“零起点挑战赛”,参赛者是一个从静止开始下落的物体。想象一下,你站在一个无风、真空且没有其他外力干扰的神秘星球上,手中握着一颗被轻轻松开的小石子。在这一刻,小石子仿佛获得了参加这场特殊比赛的入场券,它的初始速度为零,也就是说,在放手那一刻,它并没有向前冲刺或向后跳跃,而是完全静止。
-
而唯一影响小石子运动的因素就是这个星球自带的强大重力,就像一位公正无私的裁判,只给每位选手提供一致的向下牵引力。于是乎,在这“零起点挑战赛”中,小石子便开始了它的自由落体之旅,沿着垂直向下的直线路径加速坠落,上演了一场不受任何复杂因素干扰、纯粹由重力驱动的精彩表演!
(二)性质
-
自由落体运动就像是物理世界的“垂直马拉松”,只不过参赛者们不是靠双脚奔跑,而是由万有引力这位大导演亲自指挥下落。想象一下,一颗苹果从静止在枝头开始,受到地球妈妈那恒定不变的吸引力(重力加速度 g g g)后,瞬间开启了它的向下冲刺之旅。
-
这场垂直比赛中的所有选手,不论质量大小,都享有相同的加速待遇——每秒钟速度增加约9.8米/秒(在地球上)。所以,自由落体运动本质上就是一场公平公正、且全程保持匀加速直线前进的“空中芭蕾”,每位舞者无一例外地按照剧本 a = g a = g a=g的规定动作,优美而精准地下降着,上演了一场物理学舞台上的精彩表演!
(三)公式
1、速度公式
-
自由落体运动的速度公式 v t = g t v_t=gt vt?=gt就像物理世界的“速度计时器”。想象一下,你手中握着一个从静止开始下坠的小球,而万有引力是那位掌控时间的魔术师。
-
这个公式告诉我们,在任意时刻 t t t,小球下落的速度 v t v_t vt?会随着与重力加速度 g g g相乘的时间 t t t逐渐累积。也就是说,每经过一秒钟,小球的速度就会增加9.8米/秒(在地球表面)。所以,只要启动了这场垂直赛跑,无论小球质量大小,它都会像被上了发条的时钟一样,按照严格的数学规律——每过一秒就加速9.8米/秒地向下狂奔,就如同一位精准无误的“自由落体速度播报员”!
2、位移公式
-
自由落体运动的位移公式 s = 1 2 g t 2 \displaystyle s= \frac{1}{2}gt^2 s=21?gt2就像是一部物理世界的“时空计算器”。想象一下,你正在玩一个超现实版的弹射游戏,把一个小球从零高度放手让它垂直下落。这个小球在重力大魔法师(g)的影响下,每秒钟都会像坐上了免费加速电梯一样增加9.8米/秒的速度。
-
而我们的时空计算器就记录着小球与地面越来越近的亲密接触过程:时间(t)每走过一秒,小球下落的距离并不是简单的线性增长,而是像积攒能量般呈平方关系累积。所以,在这段时间内,小球累计下降的距离就像是把重力加速度(g)和时间(t)相乘后,再大方地给你打了个五折(乘以 1 2 \displaystyle \frac{1}{2} 21?),这就是它经过 t t t秒后距离地面的神奇距离 s s s啦!
3、速度位移公式
-
自由落体运动的速度位移公式 v t 2 = 2 g s v_t^2=2gs vt2?=2gs,就像是物理世界里的一首神秘诗歌,揭示了速度与高度之间的亲密关系。想象一下,你正在一个没有空气阻力的星球上,手中握着一颗神奇的石子准备进行一场垂直投掷。
-
在这个奇妙的情境中,当你把石子从某一高度 s s s处释放,它就像被赋予了生命般开始自由下坠。而这个公式就像石子在空中吟唱的歌谣,告诉我们:当石子落地瞬间(即末速度 v t v_t vt?),其速度的平方恰好等于重力加速度 g g g乘以它起始时离地面的高度的两倍。
-
换句话说,在这场垂直版“速度与激情”的演出中,无论石子起跳的位置有多高,只要我们知道了重力常数和最终速度,或者已知重力和高度,就能通过这首“速度位移之歌”计算出它落地前那一刹那的速度快慢,是不是很有趣又神奇呢?
十、运动图像
- 运动图像就像物理世界的动画片,生动展现了物体运动的动态故事。在位移图像(s-t)中,斜率“偷偷告诉你”物体那一刻的速度快慢,直线代表匀速稳定,曲线则揭示了速度的变化多端;当它穿越横轴,意味着物体完成了一次空间跨越。而在速度图像(v-t)里,每一帧画面直接显示瞬时速度,而整个剧情的进展——位移大小,则藏在图像与时间轴所围成的面积之中;切线一出,加速度立现,直线表示匀变速或恒定速度,曲线则意味着速度变化不拘一格,曲折离奇!
(一)位移图像(s-t图像)
- 图像上一点切线的斜率表示该时刻所对应速度;
- 图像是直线表示物体做匀速直线运动,图像是曲线则表示物体做变速运动;
- 图像与横轴交叉,表示物体从参考点的一边运动到另一边。
(二)速度图像(v-t图像)
- 在速度图像中,可以读出物体在任何时刻的速度;
- 在速度图像中,物体在一段时间内的位移大小等于物体的速度图像与这段时间轴所围面积的值。
- 在速度图像中,物体在任意时刻的加速度就是速度图像上所对应的点的切线的斜率。
- 图线与横轴交叉,表示物体运动的速度反向。
- 图线是直线表示物体做匀变速直线运动或匀速直线运动;图线是曲线表示物体做变加速运动。
十一、案例演示
- 有一个做匀变速直线运动的质点,它在两个连续相等的时间间隔内通过的位移分别为
24
m
24m
24m和
64
m
64m
64m,每一个时间间隔为
4
s
4s
4s,求质点在这两段位移上的初速度、末速度和加速度大小。

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- nginx反向代理实践指南:访问Tomcat
- 百题千解计划【CSDN每日一练】“鬼画符门之点点大阵”:小艺师从鬼画符门派,由于学艺不精只能画点点大阵。 一天师父要求小艺画多重点点大阵...使用Python、JavaScript等解决 | 附面试题
- 基于SSM的文化遗产的保护与旅游开发设计与实现
- SpringBoot项目处理 多数据源问题(把本地库数据 推送 到另外一个平台的库)
- 计算机Java项目|基于SSM的微课学习系统
- 优质全套Spring全套教程
- 基于Java的少儿编程网站的设计与实现
- 未来三年,BIM如何应用、落地?
- WebGL开发建筑和设计教育应用
- 轻松祛除烦人水印:三款简单易用的图片去水印工具介绍