Self-Attention的学习
文章目录
Self-Attention
模型的输入与输出
输入:输入是一个向量,输入是一个向量集。
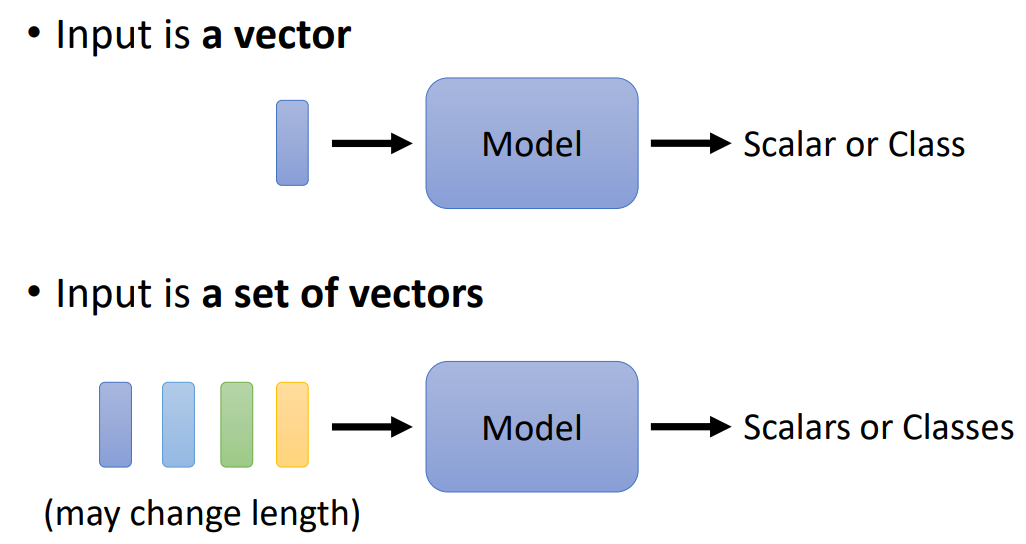
可以做为向量集的数据有:词嵌入(Word Embedding)、语音数据、图连接。
输出:一个向量对应一个标签,整个序列有一个标签,模型决定了标签的数量(seq2seq)
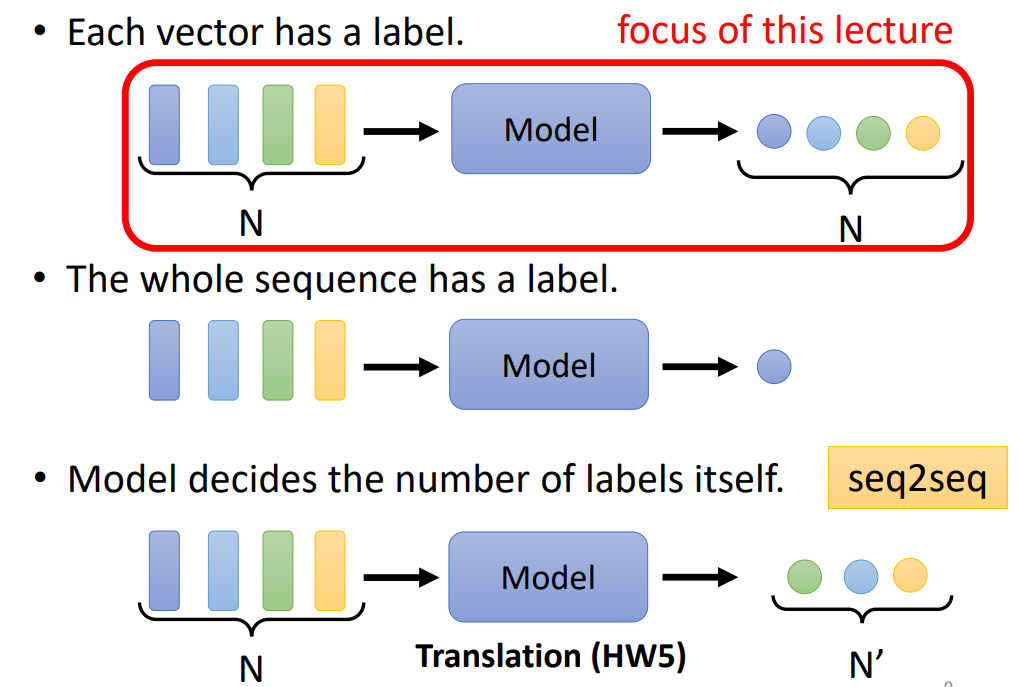
1.为什么引入Self-Attention?
在考虑上下文时,尽管全连接层能够考虑周边的一些信息,但是如果序列足够长的话,全连接的窗口不可能覆盖整个序列,因此需要自注意力机制。
只要数据可以表示为一个向量集,那么就可以使用self-attention,Self-attention可以用于语音处理,也可以用于图像。
2.Self-attention(重点)
2.1 整体架构
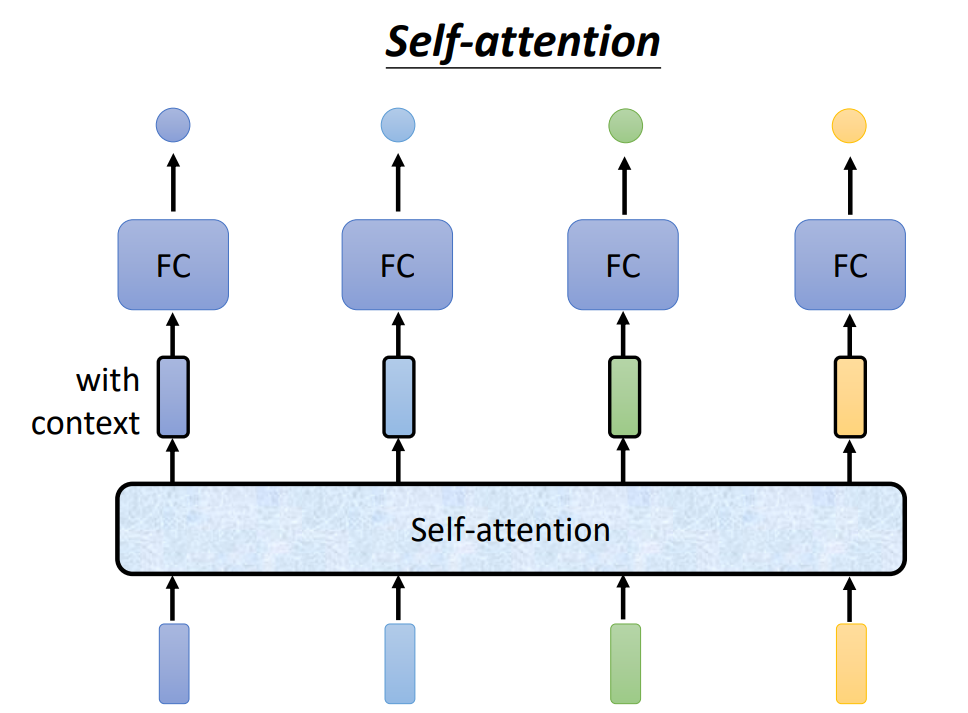
self-attention不是仅关注了当前的输入,而是关注了整体的输入。通过计算当前输入与其他输入的相关性,来共同决定当前的输出。
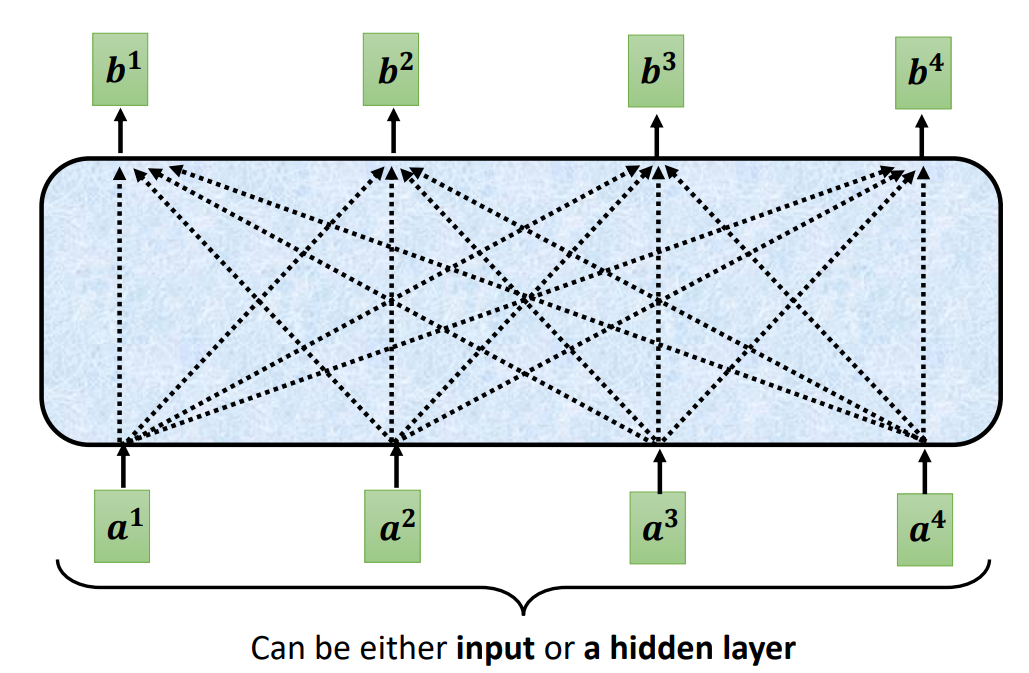
那么在整个序列中找到相关性的向量就变得很重要了。
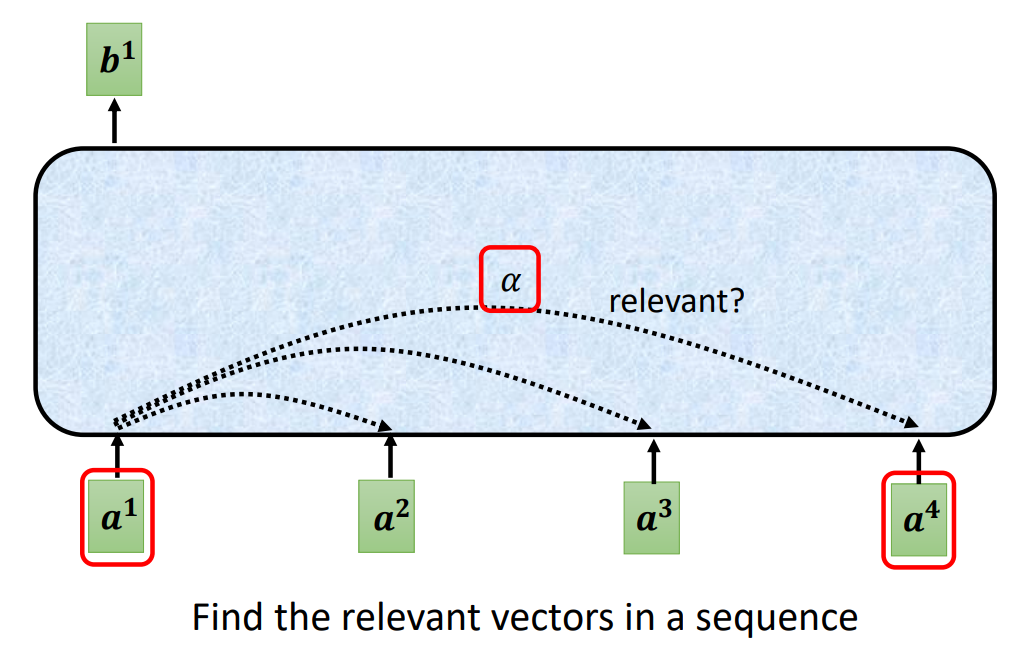
计算相关性的方式有很多,下面是两种常见的方法:

2.2 计算单个输出的原理
计算 b 1 b^1 b1的过程:
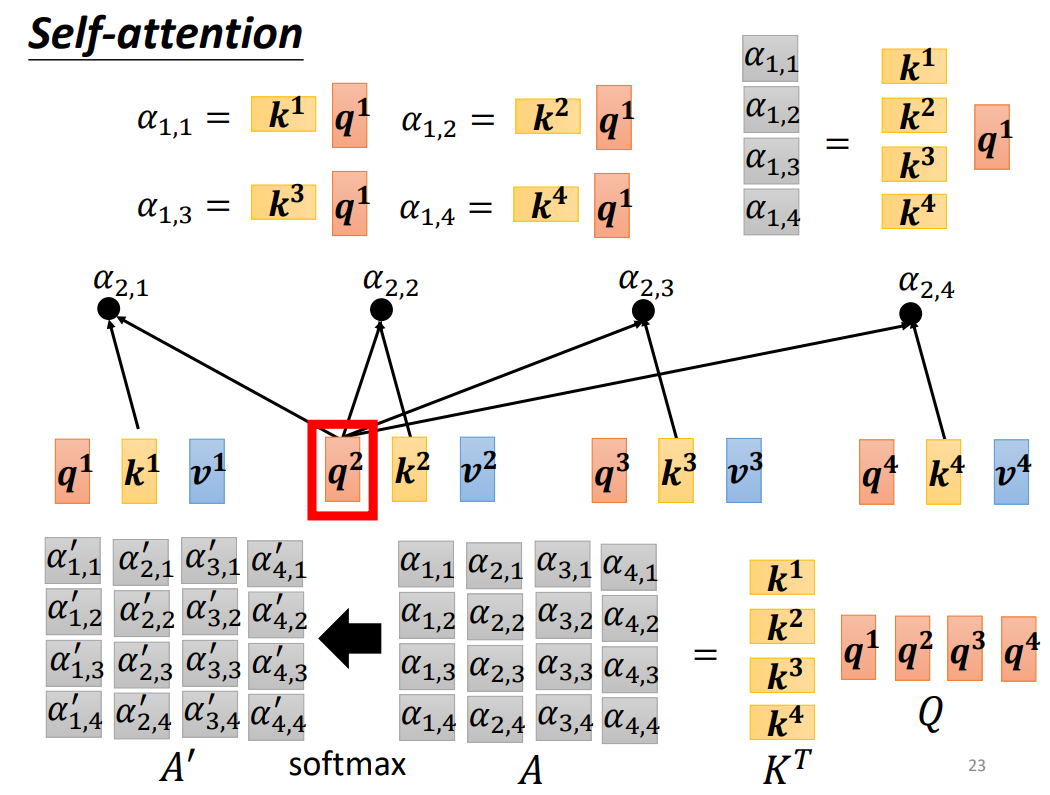
- 首先对于 a 1 a^1 a1,将 a 1 a^1 a1与 W q W^q Wq进行乘积,得到 q 1 q^1 q1,然后剩余的输入,通过乘以 W k W^k Wk计算出 k 2 , k 3 , k 4 k^2,k^3,k^4 k2,k3,k4。之后将计算的 q 1 q^1 q1与 k 2 , k 3 , k 4 k^2,k^3,k^4 k2,k3,k4分别进行点积,就分别得到了 a 2 a^2 a2对 a 1 a^1 a1, a 3 a^3 a3对 a 1 a^1 a1, a 4 a^4 a4对 a 1 a^1 a1的注意力分数 α 1 , 2 , α 1 , 3 , α 1 , 4 \alpha_{1,2},\alpha_{1,3},\alpha_{1,4} α1,2?,α1,3?,α1,4?。
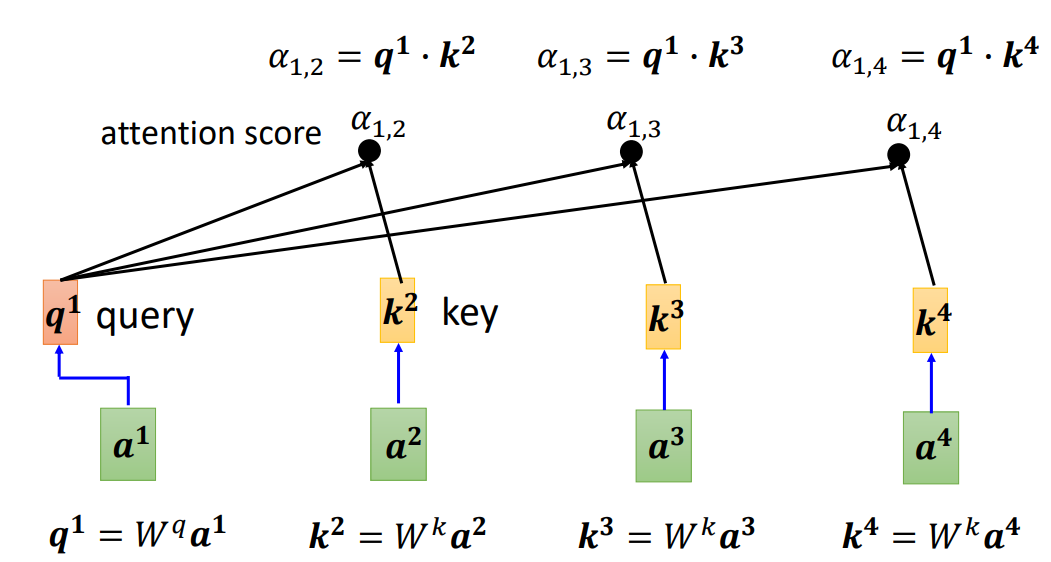
- 对于 a 1 a^1 a1我们也让其乘以 W k W^k Wk,得到 k 1 k^1 k1,通过 q 1 q^1 q1与 k 1 k^1 k1进行点积,得到 α 1 , 1 \alpha_{1,1} α1,1?。然后将 α 1 , 1 , α 1 , 2 , α 1 , 3 , α 1 , 4 \alpha_{1,1},\alpha_{1,2},\alpha_{1,3},\alpha_{1,4} α1,1?,α1,2?,α1,3?,α1,4?送入到一个Soft-Max,得到了 α 1 , 1 ′ , α 1 , 2 ′ , α 1 , 3 ′ , α 1 , 4 ′ \alpha^{'}_{1,1},\alpha^{'}_{1,2},\alpha^{'}_{1,3},\alpha^{'}_{1,4} α1,1′?,α1,2′?,α1,3′?,α1,4′?.
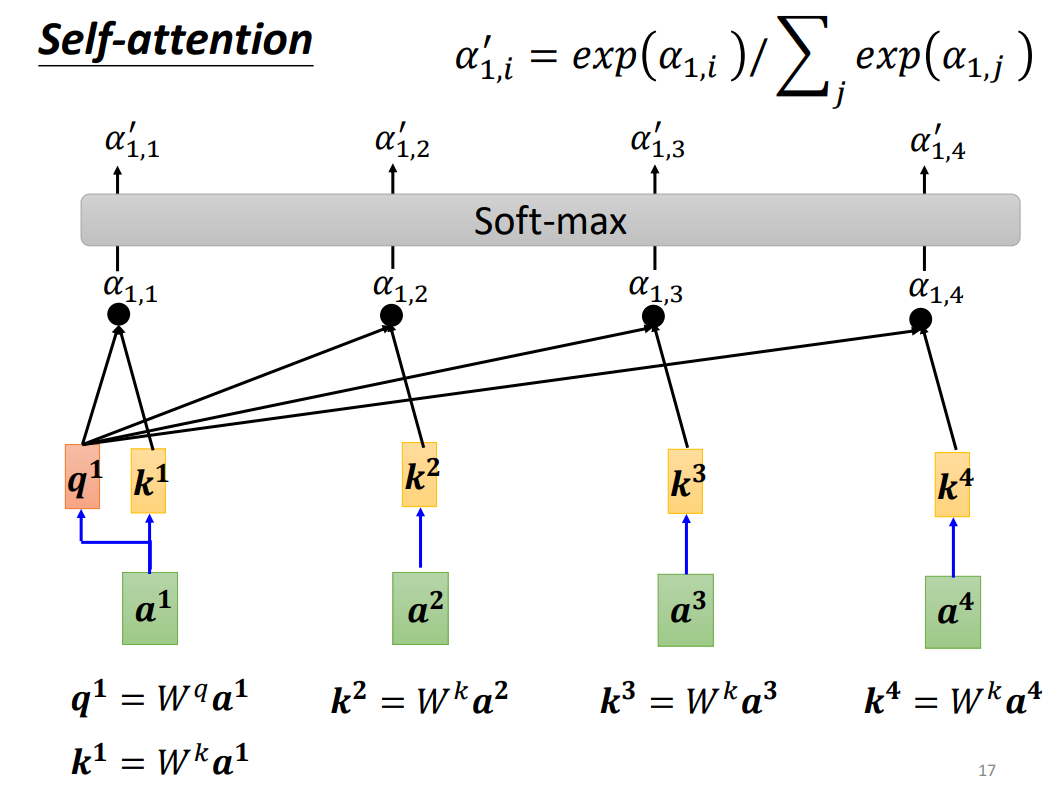
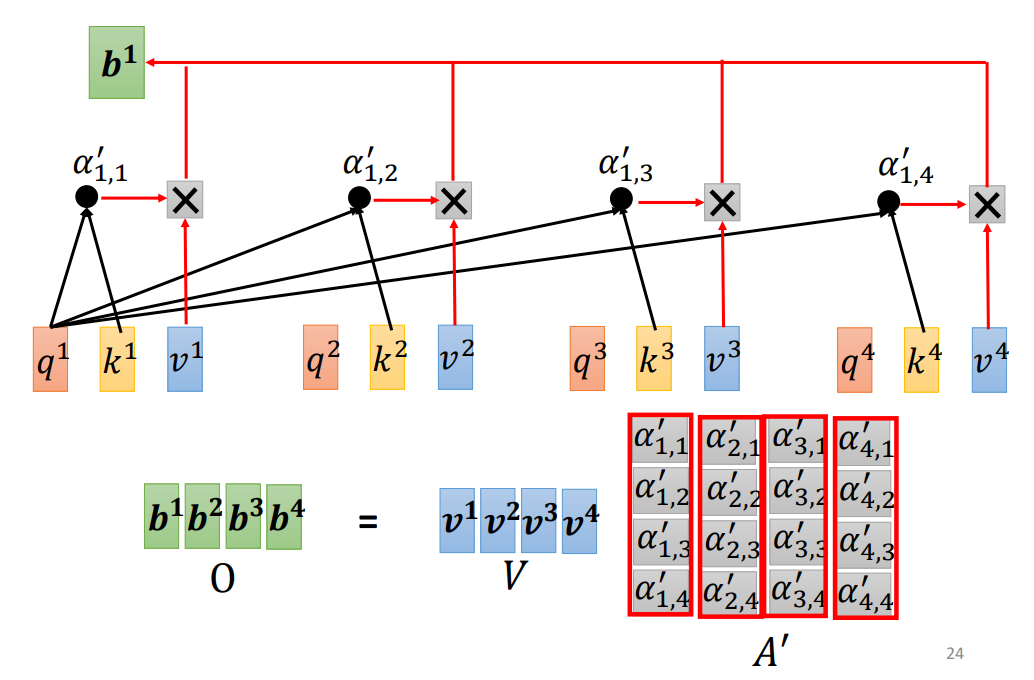
- 然后对于每一个 a 1 , a 2 , a 3 , a 4 a^1,a^2,a^3,a^4 a1,a2,a3,a4通过乘以 W v W^v Wv计算出 v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4.接下来将计算出来的 v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4分别乘以对应的注意力权重 α 1 , 1 ′ , α 1 , 2 ′ , α 1 , 3 ′ , α 1 , 4 ′ \alpha^{'}_{1,1},\alpha^{'}_{1,2},\alpha^{'}_{1,3},\alpha^{'}_{1,4} α1,1′?,α1,2′?,α1,3′?,α1,4′?并进行求和,就得到了 b 1 b^1 b1.
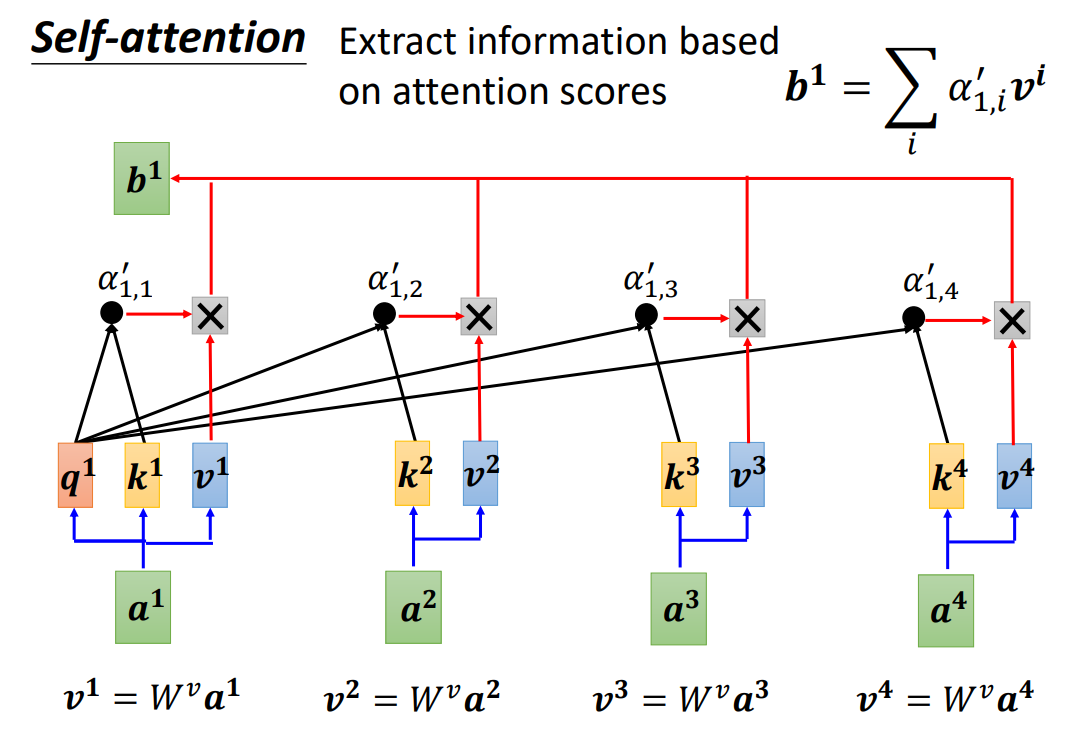
- b 2 , b 3 , b 4 b^2,b^3,b^4 b2,b3,b4也是同样的道理。

2.3 整体的矩阵计算
- 首先将每一个 a 1 , a 2 , a 3 , a 4 a^1,a^2,a^3,a^4 a1,a2,a3,a4(也就是矩阵 I I I)都分别乘以 W q , W k , W v W^q,W^k,W^v Wq,Wk,Wv,就得到了 q 1 , q 2 , q 3 , q 4 q^1,q^2,q^3,q^4 q1,q2,q3,q4(矩阵Q), k 1 , k 2 , k 3 , k 4 k^1,k^2,k^3,k^4 k1,k2,k3,k4(矩阵K), v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4(矩阵V)
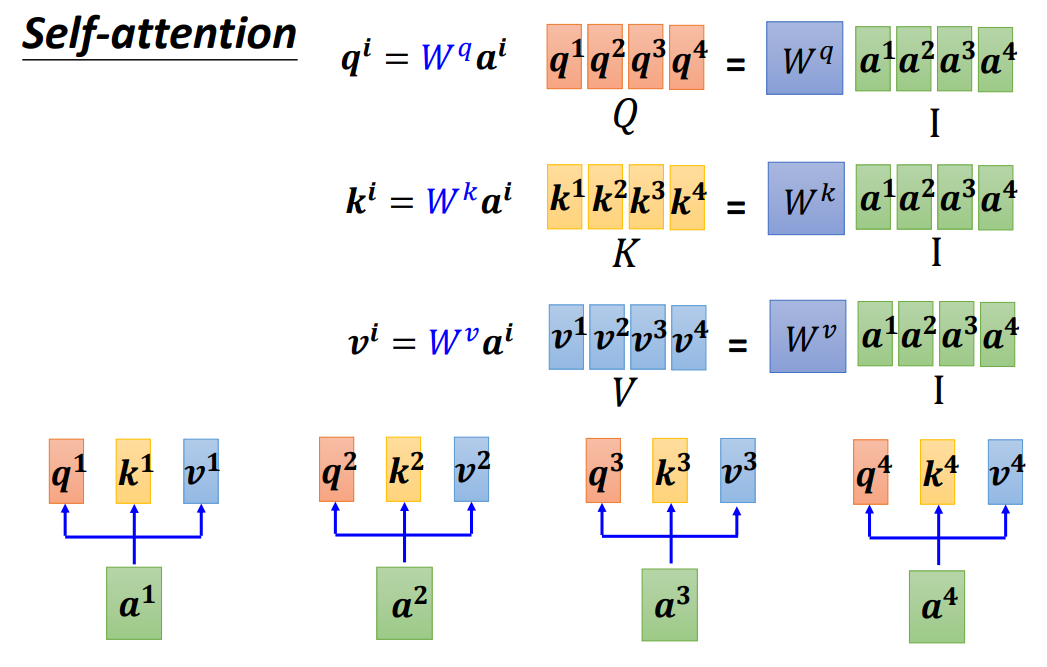
- 然后用矩阵Q乘以矩阵K就得到了矩阵A(也就是注意力矩阵),最后将矩阵A送入Softmax,就得到了 A ′ A^{'} A′
- 接着将 A ′ A^{'} A′与V相乘,就得到了矩阵O(代表输出)
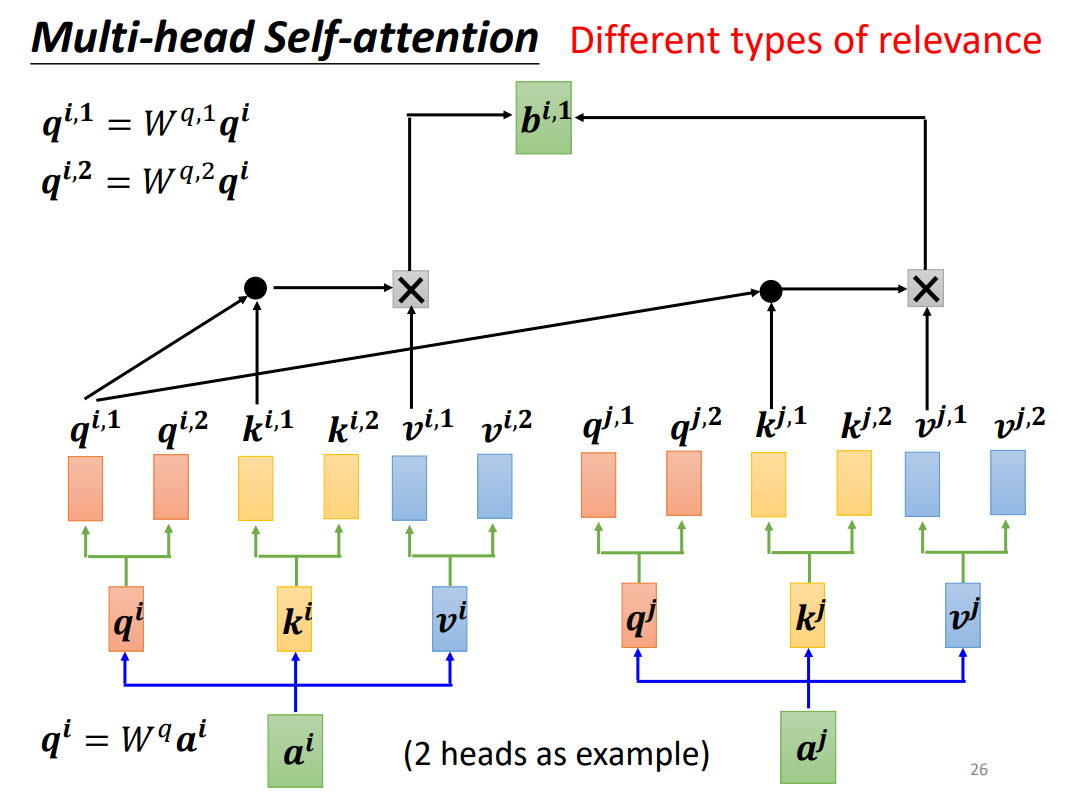
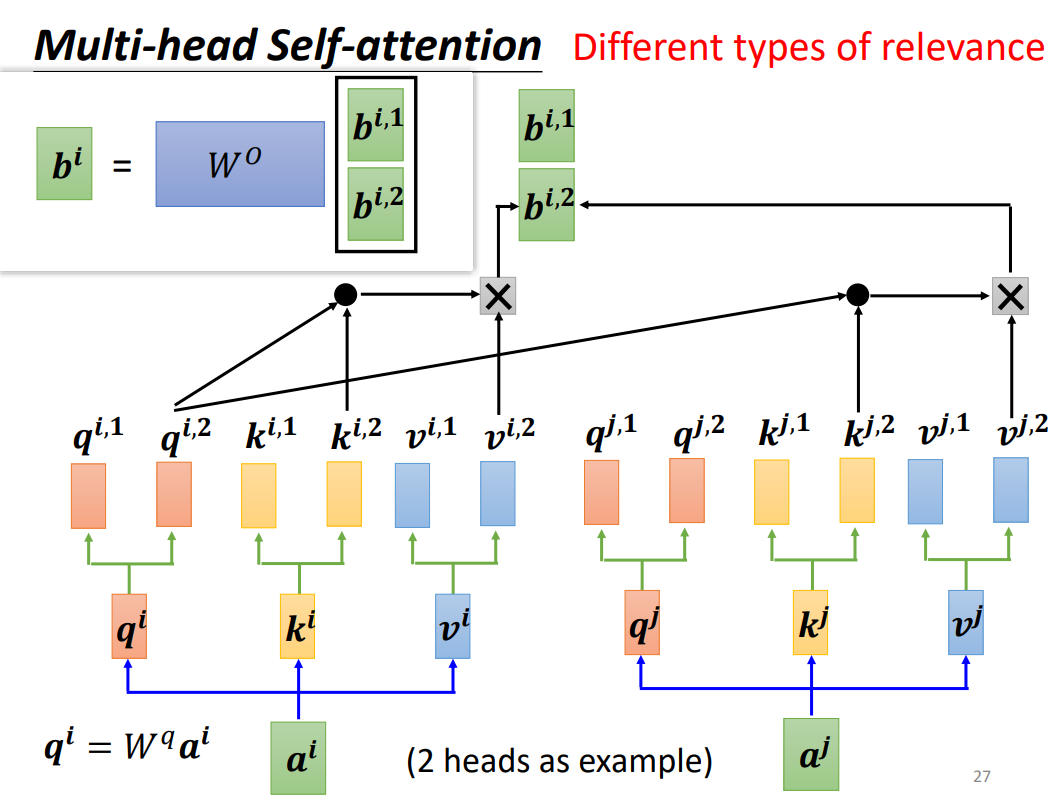
3.Multi-head Self-attention
多头自注意力原理和自注意力的原理是一致的,感觉就像是针对每一个输出,进行了多次的计算,然后将每一次计算出来的结果通过权重的方式将它们联系起来。
4.Self-attention的缺点
比如在做词性标记的时候,往往句首的词性是动词的概率较低,所以也需要考虑到位置的信息,但是Self-attention没有位置信息,上面的 a 1 , a 2 , a 3 , a 4 a^1,a^2,a^3,a^4 a1,a2,a3,a4标号是为了理解而标记上去的,实际上它们之间的位置信息是不确定的,没有说谁就在谁的前面或者后面。
改进:可以通过position encoding的技术来实现位置信息。就是在每一个位置引入一个位置向量 e i e^i ei,不同位置的 e i e^i ei是不一样的。通过 e i e^i ei来告诉不同位置的位置信息。
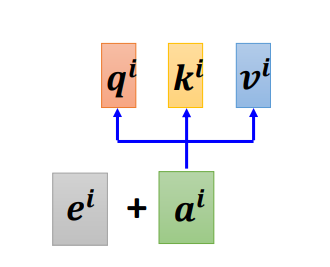
目前position representation的方法很多,不用仅仅局限于上面的 e i e^i ei.
5.Self-attention与CNN的对比
Self-attention就是一种复杂的CNN,反过来说,CNN是一种简单的self-attention.
CNN 每次关注的是一个 receptive field(这个域的范围是由我们自己决定的),而self-attention关注的是整体的域。CNN是每次从这个较小的域中找到关键信息,而self-attention是从整体的域中去计算他们之间的相关程度,找出重要的特征信息。
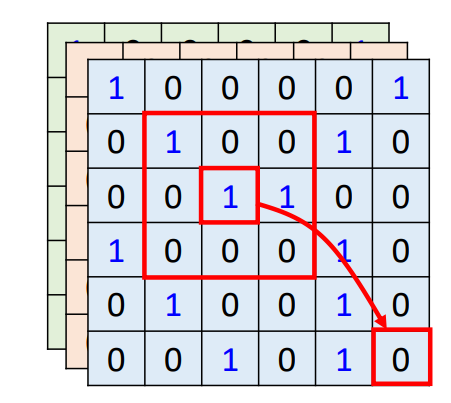
在数据量较少的情况下,CNN的效果较好,但是在数据量较多的情况下,self-attention的效果优于CNN。
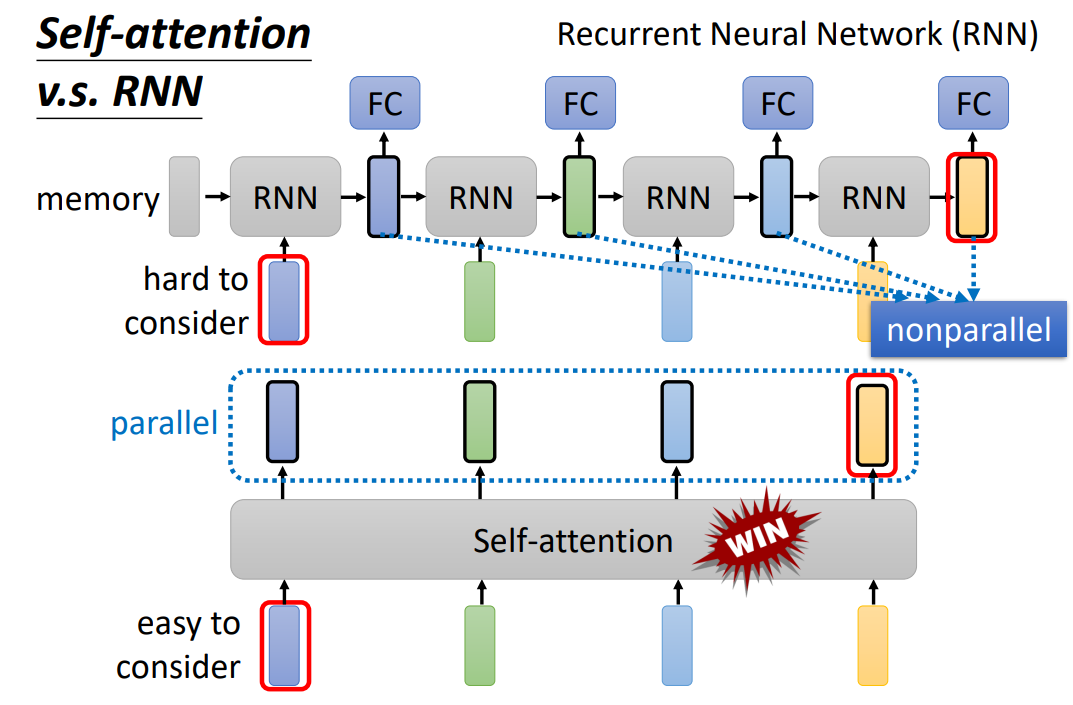
6.Self-attention与RNN的对比
尽管Self-attention与RNN都是用于时序数据,Self-attention的输出是并行输出,但是RNN的输出不是并行的。self-attention的效果要优于RNN。
这篇笔记根据李宏毅老师的讲解结合自己的理解所写。感兴趣的伙伴可以去听李宏毅老师的课程,讲的十分通透。链接如下:
【强烈推荐!台大李宏毅自注意力机制和Transformer详解!】 https://www.bilibili.com/video/BV1v3411r78R/?share_source=copy_web&vd_source=a36f62f9fcd2efea97449039538032fa
😃😃😃
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!