NOIP2014提高组day2-T2：寻找道路

题目链接

[NOIP2014 提高组] 寻找道路

题目描述

在有向图 $G$ 中，每条边的长度均为 $1$，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1. 路径上的所有点的出边所指向的点都直接或间接与终点连通。
2. 在满足条件 $1$ 的情况下使路径最短。

注意：图 $G$ 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入格式

第一行有两个用一个空格隔开的整数 $n$ 和 $m$，表示图有 $n$ 个点和 $m$ 条边。

接下来的 $m$ 行每行 $2$ 个整数 $x,y$，之间用一个空格隔开，表示有一条边从点 $x$ 指向点 $y$。

最后一行有两个用一个空格隔开的整数 $s,t$，表示起点为 $s$，终点为 $t$。

输出格式

输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。如果这样的路径不存在，输出 $?1$。

样例 #1

样例输入 #1

3 2
1 2
2 1
1 3

样例输出 #1

-1

样例 #2

样例输入 #2

6 6
1 2
1 3
2 6
2 5  
4 5
3 4
1 5

样例输出 #2

3

提示

样例 1 解释

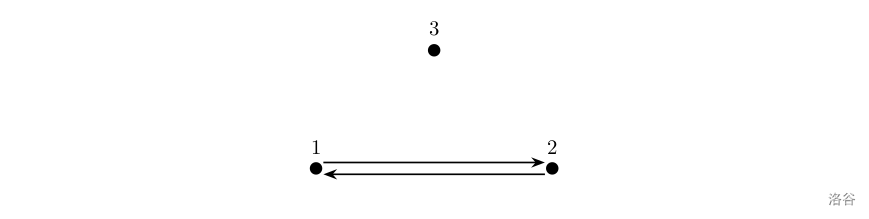
如上图所示，箭头表示有向道路，圆点表示城市。起点 $1$ 与终点 $3$ 不连通，所以满足题目描述的路径不存在，故输出 $?1$。

样例 2 解释

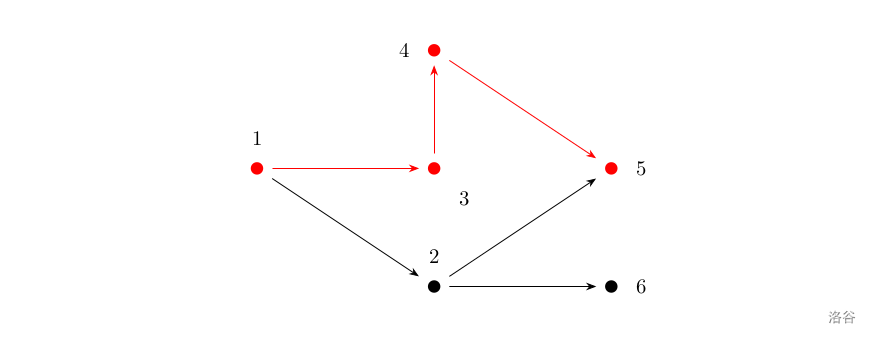
如上图所示，满足条件的路径为 $1\to 3\to 4\to 5$。注意点 $2$ 不能在答案路径中，因为点 $2$ 连了一条边到点 $6$，而点 $6$ 不与终点 $5$ 连通。

数据范围及约定

• 对于 $30\%$ 的数据，$0<n\le 10$，$0<m\le 20$。
• 对于 $60\%$ 的数据，$0<n\le 100$，$0<m\le 2000$。
• 对于 $100\%$ 的数据，$0<n\le 10^4$，$0<m\le 2\times 10^5$，$0<x,y,s,t\le n,x,s\ne t$。

算法思想

根据题目描述，要求的是满足下面条件的最短路径的长度：

• 路径上的所有点的出边所指向的点都直接或间接与终点连通

也就是说，该路径上的每个点都能走到终点。那么有哪些点满足条件呢？

• 首先可以从终点开始反向搜索所有能够达到的点$i$，将其状态$st[i]$设置为true
• 其次遍历每个点$i$，如果其所有出边所指向的点的状态都为true，那么点$i$满足条件

当筛选出来所有满足条件的点后，可以通过bfs求起点到终点的最短路径了。

注意，由于正向和反向都要处理，因此需要双向建边，那么如何区分正向边和反向边呢？可以使用链式前向星来保存图，按顺序添加边时，偶数为正向边，奇数为反向边。

时间复杂度

• 从终点开始反向搜索所有能够达到的点，每条边只会遍历一次，时间复杂度为$O(n+m)$。
• 遍历每个点，处理其所有出边，时间复杂度为$O(n+m)$
• bfs求最短路径，时间复杂度为$O(n+m)$

代码实现

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e4 + 5, M = 4e5 + 5;
int h[N], e[M], ne[M], idx;
int dis[N];
bool st[N], f[N];
void add(int a, int b)  // 添加一条边a->b
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ; //正向边是偶数，反向边是奇数
}

void dfs(int u)
{
    st[u] = true;
    for(int i = h[u]; ~ i; i = ne[i])
    {
        if(i % 2 == 0) continue; //只搜索反向边
        int v = e[i];
        if(!st[v]) dfs(v);
    }
}

int bfs(int s, int t)
{
    if(!f[s]) return -1; //起点不满足条件
    memset(dis, 0x3f, sizeof dis);
    queue<int> q;
    q.push(s), dis[s] = 0;
    while(q.size())
    {
        int u = q.front(); q.pop();
        if(u == t) return dis[u];
        for(int i = h[u]; ~ i; i = ne[i])
        {
            if(i % 2) continue; //只搜索正向边
            int v = e[i];
            if(!f[v]) continue; //不满足条件
            if(dis[v] > dis[u] + 1)
            {
                dis[v] = dis[u] + 1;
                q.push(v);
            }
        }
    }
    return -1;
}

int main()
{
    int n, m, s, t;
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a); //双向建边
    }
    scanf("%d%d", &s, &t);
    dfs(t); //反向搜索每个点的状态
    //处理每个点出边所指向的点
    for(int i = 1; i <= n; i ++)
    {
        f[i] = true;
        for(int j = h[i]; ~ j; j = ne[j])
        {
            //只判断正向边
            if(j % 2 == 0 && !st[e[j]])
            {
                f[i] = false; //i点不满足条件
                break;
            }
        }
    }
    //搜索最短路径
    printf("%d\n", bfs(s, t));
    return 0;
}