每周一算法:区间覆盖
问题描述
给定 N N N个闭区间 [ a i , b i ] [a_i,b_i] [ai?,bi?],以及一个线段区间 [ s , t ] [s,t] [s,t],请你选择尽量少的区间,将指定线段区间完全覆盖。
输出最少区间数,如果无法完全覆盖则输出 ? 1 -1 ?1。
输入格式
第一行包含两个整数 s s s和 t t t,表示给定线段区间的两个端点。
第二行包含整数 N N N,表示给定区间数。
接下来 N N N行,每行包含两个整数 a i , b i a_i,b_i ai?,bi?,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需最少区间数。
如果无解,则输出 ? 1 -1 ?1。
数据范围
1 ≤ N ≤ 1 0 5 1≤N≤10^5 1≤N≤105, ? 1 0 9 ≤ a i ≤ b i ≤ 1 0 9 -10^9≤a_i≤b_i≤10^9 ?109≤ai?≤bi?≤109,
? 1 0 9 ≤ s ≤ t ≤ 1 0 9 -10^9≤s≤t≤10^9 ?109≤s≤t≤109
输入样例
1 5
3
-1 3
2 4
3 5
输出样例
2
算法思想
从测试样例分析,要覆盖线段区间 [ 1 , 5 ] [1,5] [1,5],只需要 2 2 2个闭区间 [ ? 1 , 3 ] [-1,3] [?1,3]和 [ 3 , 5 ] [3,5] [3,5],如下图所示。
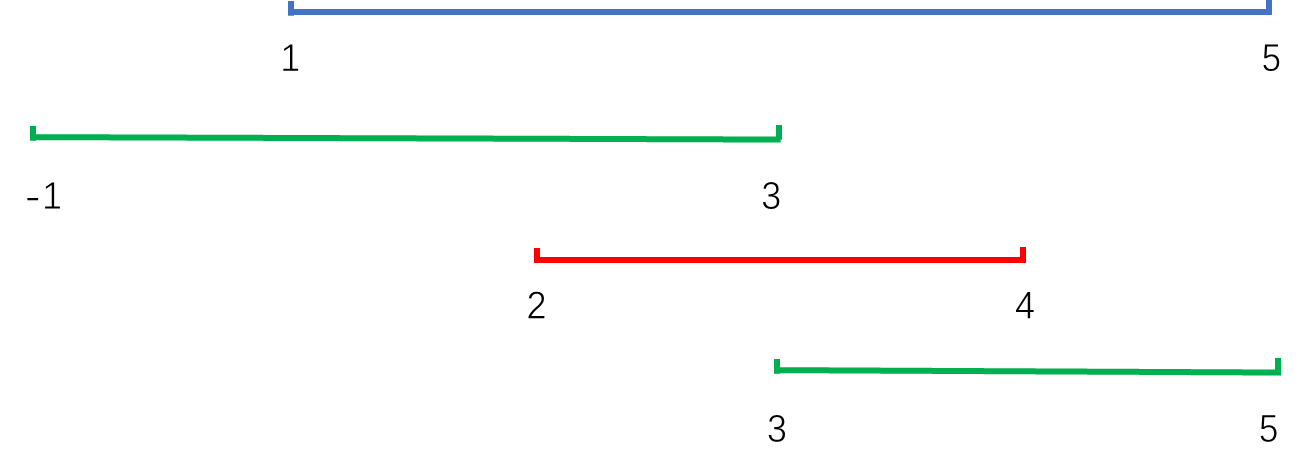
可以采用贪心的思想来解决这个问题:
- 首先将 N N N个闭区间 [ a i , b i ] [a_i,b_i] [ai?,bi?]按左端点排序
- 从前向后遍历每个区间
- 在所有能覆盖线段区间 [ s , t ] [s,t] [s,t]左端点 s s s的区间中,选择右端点最大的区间 [ a j , b j ] [a_j,b_j] [aj?,bj?],其中 a j ≤ s a_j\le s aj?≤s,表示能够覆盖点 s s s。
- 然后将 s s s更新成所有满足条件的区间中右端点的最大值
- 重复上述过程,直到 s ≥ t s\ge t s≥t,表示线段区间被完全覆盖
时间复杂度
- 将 n n n个区间排序的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
- 从前向后遍历每个区间,由于每个区间仅会处理 1 1 1次,因此时间复杂度为 O ( n ) O(n) O(n)
总的时间复杂度为 O ( n + n l o g n ) O(n + nlogn) O(n+nlogn)
代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
typedef pair<int, int> PII;
PII st[N];
int main()
{
int s, t, n, ans = 0, flag = 0;
cin >> s >> t >> n;
for(int i = 0; i < n; i ++) cin >> st[i].first >> st[i].second;
//排序
sort(st, st + n);
for(int i = 0; i < n; i ++)
{
//在所有能覆盖线段左端点s的区间中,选择右端点最大的区间
int j = i, R = -1e9;
while(j < n && st[j].first <= s) R = max(R, st[j ++].second);
//无法覆盖左端点s
if(R < s) break;
ans ++; //需要的区间个数增加1
s = R; //更新要覆盖的左端点
if(s >= t) //覆盖完成
{
flag = 1;
break;
}
i = j - 1; //继续从当前区间向后遍历
}
if(flag) cout << ans;
else cout << -1;
return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【离散数学】xjtu版离散复习攻略
- 算法设计与分析 | 动态规划(最长公共子序列)
- 盘点三款服务器运维工具
- QC/PD快充电源产品应用介绍
- 银行接口测试学习笔记:接口测试从分析到设计!
- 前端性能优化三十七:花裤衩模板路由懒加载
- 招投标系统简介 企业电子招投标采购系统源码之电子招投标系统 —降低企业采购成本
- brew 安装openapi-generator提示@@HOMEBREW_JAVA@@/bin/java: No such file or directory
- 专属配方重磅发布,蒙牛悠瑞开创中老年奶粉新征程
- Vue 3 语法和特性