【算法】算法(模拟、指针等)解决字符串类题目(C++)
发布时间:2024年01月15日
1. 前言
字符串题目有很多种,这里筛选几个考察模拟、双指针等的题目,并用相关算法解决。
2. 解决 字符串类算法题
14.最长公共前缀

思路
- 题意分析:题目要求找到字符串数组中的最长公共前缀。
- 解法一:两两比较
- 遍历数组,每次比较后更新最长公共前缀,并循环比较找最长公共前缀
- 解法二:统一比较
- 遍历第一个字符串的所有字符,将当前字符与其他字符串相同位置的字符进行比较。
- 如果发现不匹配的字符或某个字符串已经达到最终长度(即没有更多字符可比较),则返回第一个字符串的前缀子串
代码
- 解法一:
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
string ret = strs[0];
// 解法一:两两比较,找公共前缀
for(int i = 0; i < strs.size(); i++)
{
ret = findCommonPrefix(ret, strs[i]);
}
return ret;
}
string findCommonPrefix(string &s1, string& s2) {
// 找公共前缀
string tmp = "";
for(int i = 0; i < min(s1.size(), s2.size()); ++i)
{
if(s1[i] == s2[i])
tmp += s1[i];
else
break;
}
return tmp;
}
};
- 解法二:
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
// 解法二:统一比较
for(int i = 0; i < strs[0].size(); ++i) // 遍历第一个字符串的所有字符
{
char tmp = strs[0][i]; // tmp与其他字符比较
for(int j = 0; j < strs.size(); ++j)
{
if(tmp != strs[j][i] || i == strs[j].size()) // 如果字符不匹配or有字符串最终长度截止到当前位置
return strs[0].substr(0, i);
}
}
return strs[0];
}
};
5.最长回文子串

思路
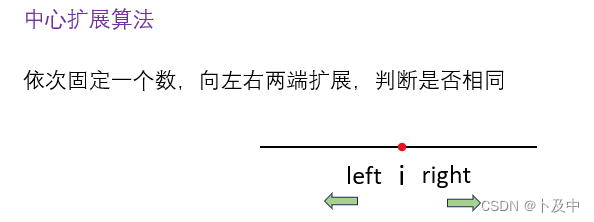
- 解法:中心扩展算法
- 如图所示,我们遍历数组,依次固定数组每一位,通过左右两指针找最长回文串。
- 细节注意:
- 奇数长的回文串与偶数长的回文串计算时,两指针起始位置不同,所以我们分别进行计算。

- 奇数长的回文串与偶数长的回文串计算时,两指针起始位置不同,所以我们分别进行计算。
代码
string longestPalindrome(string s) {
// 遍历每一位,双指针按从左右方向移动,并比较
int len = 0, n = s.size(), begin = 0; // begin存储最长子串的开始位置
for(int i = 0; i < n; ++i)
{
// 进行奇数长回文串的操作判定
int left = i, right = i;
while((left >= 0 && right <= n) && s[left] == s[right]) // 左右指针每次各移一步
left--, right++;
if(right - left - 1 > len) // 如果此时回文串长度>len,更新结果
{
len = right - left - 1;
begin = left + 1;
}
// 进行偶数长回文串的判定
left = i, right = i + 1;
while(left >= 0 && right <= n && s[left] == s[right]) // 左右指针每次各移一步
left--, right++;
if(right - left - 1 > len)
{
len = right - left - 1;
begin = left + 1;
}
}
return s.substr(begin, len);
}
67.二进制求和

思路
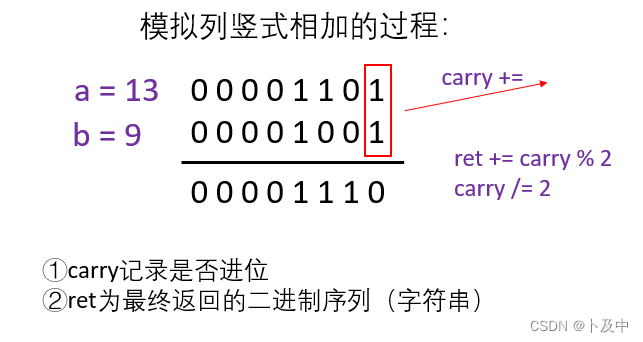
- 解法:模拟二进制列式相加的过程
- 分别用两指针遍历两字符串,每次用变量carry累加二进制每一位
- 后将此次carry加到最终结果中,carry /= 2
- 由于字符串ret是逐渐累加结果的,翻转后的字符串才是二进制顺序
代码
string addBinary(string a, string b) {
int carry = 0; // 记录是否有进位
int cur1 = a.size()-1, cur2 = b.size()-1;
string ret = "";
while(cur1 >= 0 || cur2 >= 0 || carry)
{
if(cur1 >= 0) carry += a[cur1--] - '0';
if(cur2 >= 0) carry += b[cur2--] - '0';
ret += carry % 2 + '0'; // carry%2即为相加的和
carry /= 2; // 下一位的进位
}
// 由于字符串是逐渐累加结果的,翻转后的字符串才是二进制顺序
reverse(ret.begin(), ret.end());
return ret;
}
43.字符串相乘

思路
- 题意分析:要求求出 两个字符串表示的整数 的乘积,且不得使用库函数直接进行整形和字符串的转换。
- 解法:模拟列式相乘的过程
- 与上题类似,我们对两字符串首先进行不进位相乘,
- 将输入的两个字符串逆序,从个位开始计算
- 对应位置上的数字相乘,并将结果存储在临时数组中
- 后将所有相乘结果相加
- 处理进位
- 定义一个变量carry来记录进位数,然后从数组的第一位开始,将当前位置上的数字与carry相加,得到当前位置上的数字的和,并更新carry为下一位的进位数
- 将每一位上的结果转换为字符,并添加到结果字符串ret中
- 去掉结果字符串ret的前导零,并将其逆序,得到最终的结果

- 与上题类似,我们对两字符串首先进行不进位相乘,
代码
string multiply(string num1, string num2) {
// 解法:模拟列式运算过程
// 1. 逆序字符串,从个位开始计算
reverse(num1.begin(), num1.end());
reverse(num2.begin(), num2.end());
// 2. 不进位相乘后相加
int m = num1.size(), n = num2.size();
vector<int> tmp(m + n - 1);
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
tmp[i + j] += (num1[i] - '0') * (num2[j] - '0');
// 3. 处理进位
string ret = "";
int cur = 0, carry = 0;
while(cur < m + n - 1 || carry)
{
if(cur < m + n - 1) carry += tmp[cur++]; // 记录当前位置元素
ret += (carry % 10) + '0'; // ret加上个位
carry /= 10; // 下一位的进位数
}
cout << ret;
// 4. 去掉前导0
while(ret.size() > 1 && ret.back() == '0')
ret.pop_back();
reverse(ret.begin(), ret.end());
return ret;
}
文章来源:https://blog.csdn.net/Dreaming_TI/article/details/135590323
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- paddle 54 从PaddleClas2.5初始化模型用于迁移学习(LeViT、ReXNet、EfficientNet等)
- JAVA高级技术入门(单元测试,反射,注解,动态代理)
- 快速便捷的文件压缩利器!iFastZip for Mac让压缩解压更高效
- nodejs 递归拷贝文件夹下所有的文件到一个文件夹下
- OpenCV4 工业缺陷检测的六种方法
- springboot整合shiro实现前后端分离,兼容最新的jakarta的依赖包(片尾推荐当前最好用的权限框架)
- 炸裂!这6个 PyCharm 技巧太实用!
- 第7章-第1节-Java中的异常处理
- 面试 Vue 框架八股文十问十答第四期
- 关于 Appium 各种版本的安装,都在这里