Tarjan-vDCC,点双连通分量,点双连通分量缩点
前言
双连通分量是无向图中的一个概念,它是指无向图中的一个极大子图,根据限制条件可以分为边双连通分量和点双连通分量,欲了解双连通分量需先了解Tarjan算法,以及割点割边的概念及求解。本篇博客介绍点双连通分量的相关内容。
前置知识
学习点双连通分量前,你需要先了解:
关于Tarjan:SCC-Tarjan算法,强连通分量算法,从dfs到Tarjan详解-CSDN博客
关于缩点:SCC-Tarjan,缩点问题-CSDN博客
关于割点:Tarjan-割点问题-CSDN博客
关于割边:Tarjan-割边问题-CSDN博客
点双连通分量的定义
在无向图中,存在一个极大子图,其中任意两个顶点之间连通,并且删除任意一点该子图仍然是连通的,我们称该极大子图为点双连通分量(vertex Double Connected Components,vDCC)。
推论
-
无向图中极大的不包含割点的连通分量被称为点双连通分量(vertex Double Connected Components,vDCC)。
-
一个割点存在于至少两个双连通分量之中
如下图中1、5为割点,{1,2,3,4}, {1,5},{5,6}, {5,7,8}均为vDcc
](https://img-blog.csdnimg.cn/direct/8decd7c4698849f1a88b34d48aa9e4f7.png)
Tarjan算法求解vDcc
我们回顾一下Tarjan算法涉及到的概念:
搜索树
我们dfs对图遍历,保证每个点只访问一次,访问过的节点和边构成一棵有向树,我们称之为搜索树。
强连通分量的根
如果节点x是某个强连通分量在搜索树中遇到的第一个节点,那么这个强连通分量的其余节点肯定是在搜索树中以x为根的子树中。节点x被称为这个强连通分量的根。
时间戳
我们用数组dfn[]来保存节点第一次访问时间,dfn[x]即节点x第一次访问的时间戳。
追溯值
数组low[]来记录每个节点出发能够访问的最早时间戳,记low[x]节点x出发能够访问的最早时间戳,即追溯值。
算法原理
仍然是基于Tarjan算法进行求解,其实就是Tarjan算法求解割点和强连通分量的结合。
我们Tarjan在有向图求SCC中,通过栈保存连通分量的节点,又通过时间戳和追溯值是否相等来找到强连通分量的根从而从栈中取出节点。
而求解割点时,我们对于low值更新是不允许越过父节点来更新low值的,即我们else代码段中的low[x] = min(low[x], dfn[y]);
那么我们如何来记录点双连通分量呢?
点双连通分量的记录
和求解SCC,eDCC一样,借助栈来保存节点以及取出连通分量中的点。不过与前两者不同的是,前者在完成子节点遍历后根据时间戳和追溯值判断根来取出连通分量中的节点,而vDCC要在出现一个子节点y满足low[y] >= dfn[x]时就进行vDCC的记录。为什么呢?
如下图
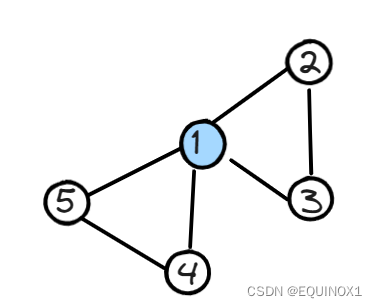
1为割点,但是点双连通分量为{1,4,5}和{1,2,3},也就是说对于一个割点它可以是多个环的环顶,所以遍历完一个环就要把这个环和割点本身记录为一个点双连通分量。
孤立点和自环的特判
孤立点
我们的图中如果有孤立点的话,其自身就是一个vDCC,所以对于孤立点我们直接给他开个单间,放到一个vDCC中,不过出不出栈无所谓,因为孤立点不影响前面的vDCC和后面的vDCC。
自环
如果是含有多个点的vDCC的话我们不用特殊处理,自然会归到相应的vDCC,但如果是孤立自环也就是说孤立点的自环的话,我们需要特判,很简单,我们tarjan求割点要记录child,对于孤立点自环child自然为0而且low[x] == dfn[x],以此特判即可,后面代码会具体实现。
算法流程
- 给x打时间戳,入栈
- 如果是孤立点,直接开单间,返回
- 否则遍历子节点y,记录child,
- low[y] >= dfn[x],child++,根据情况记录割点,然后记录vDCC
- 离开函数时特判孤立点自环
代码实现
仍然是使用链式前向星存图,关于链式前向星,详见:一种实用的边的存储结构–链式前向星-CSDN博客
#define N 500010
#define M 4000010
struct edge
{
int v, nxt;
} edges[M];
int head[N], idx = 0;
void addedge(int u, int v)
{
edges[idx] = {v, head[u]};
head[u] = idx++;
}
int n, m, dfn[N], low[N], st[N], tot = 0, cnt = 0, top = 0, root;
bitset<N> cut;
vector<int> vdcc[N];
void tarjan(int x)
{
low[x] = dfn[x] = ++tot;
st[top++] = x;
// 孤立点
if (head[x] == -1)
{
vdcc[++cnt].emplace_back(x);
return;
}
int child = 0, y;
for (int j = head[x]; ~j; j = edges[j].nxt)
{
y = edges[j].v;
if (!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x])
{
child++;
if (x != root || child > 1)
cut[x] = 1;
cnt++;
int z;
do
{
z = st[--top];
vdcc[cnt].emplace_back(z);
} while (z != y);
vdcc[cnt].emplace_back(x);
}
}
else
low[x] = min(low[x], dfn[y]);
}
// 孤立点自环
if (!child && dfn[x] == low[x])
vdcc[++cnt].emplace_back(x);
}
vDcc缩点问题
vDCC缩点相较于SCC缩点和eDCC缩点也有所不同,因为涉及到了割点的分裂,所以每个vDCC缩点后是跟割点进行相连,vDCC缩点后也会得到一棵树或森林。
代码实现如下:g为缩点图的邻接表存储
//vector<int> vdcc[N], g[N];
int num = cnt;
for (int i = 1; i <= n; i++)
if (cut[i])
id[i] = ++num;
for (int i = 1; i <= cnt; i++)
for (auto x : vdcc[i])
{
if (cut[x])
{
g[i].emplace_back(id[x]);
g[id[x]].emplace_back(i);
}
}
OJ练习
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!