python实现堆排序法

对于简单选择排序法的实现过程中发现，虽然其是一种非常符合人类思维的排序方式，但是对于其实现过程中的时间复杂度，其实是较高的，所以针对这一点，人们提出了堆排序法，对简单选择排序法进行了改进，旨在提高排序效率。

其主要实现的方法可以使用专门的库headpq，然后对给定数据进行堆排序实现如下：

import heapq
def heapSort(nums):
    result = []
    for i in range(nums):
        heapq.heapify(nums)
        result.append(nums[0])
        nums.remove(nums[0])
    return result

在讲解堆排序法的原理之前，首先要知道一个概念，那就是堆的概念，堆可以分成大根堆和小根堆。对于大根堆的两个充分必要条件是，这个堆必须是一颗完全二叉树，另一个就是对于堆中的任意一个非叶子节点，都必须满足ni不小于n2i且ni不小于n(2i+1)。这也证明了ni的值就是堆中最大的值，这也就是大根堆的名字来由。而小根堆的原理就是类似于大根堆，只是ni是堆中最小的值。

这里举例说明堆排序法的过程。

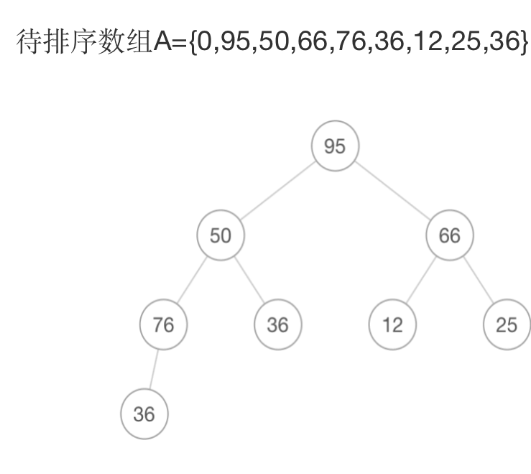
对于以上的待排序的数组，首先需要将这个数组的成员列为堆的形式，以上就是堆形式的数据。

添加图片注释，不超过 140 字（可选）

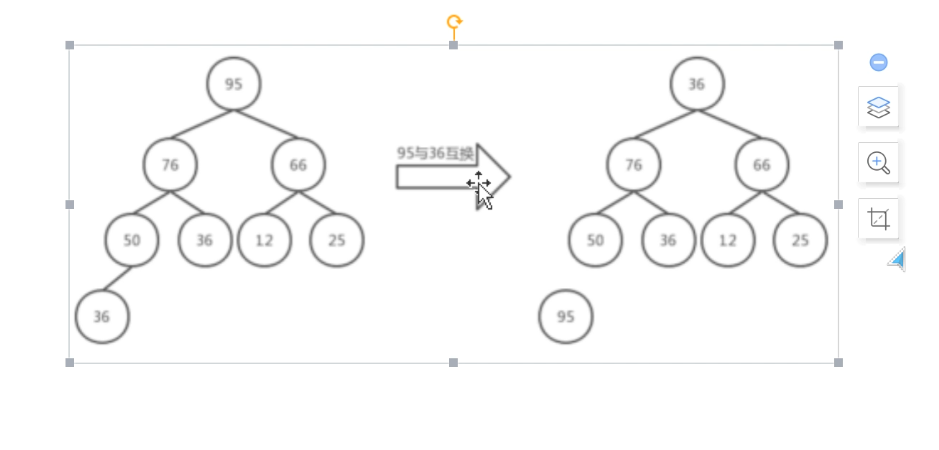
然后就是对堆进行处理，将大根堆的根节点与最后一个叶节点也就是36进行了位置更换之后，然后将前根节点95摘出来，不在堆内部，对剩下的堆进行大根堆化。

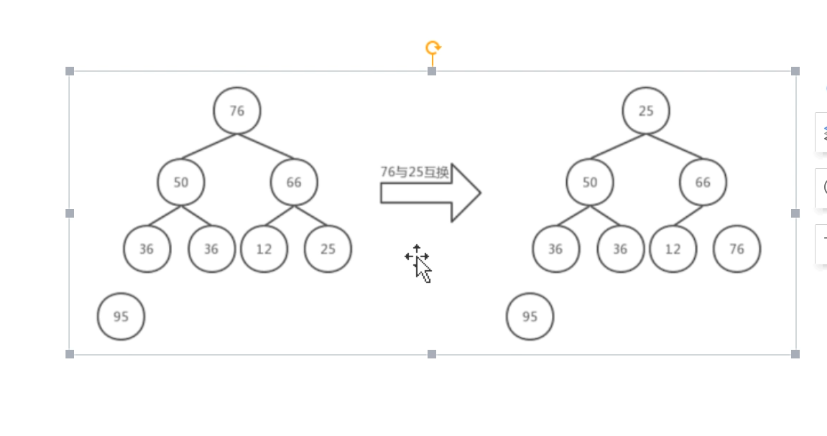
然后重复上一步的操作，调整后的大根堆的根节点是76，又使用叶节点36和76根节点位置对调，再将76前根节点摘出大根堆，就又得到一个剩余的节点树，将其调整为大根堆。

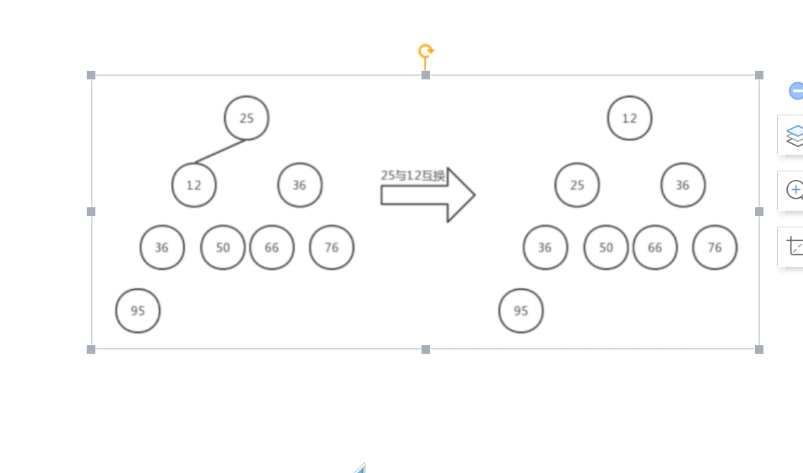
直到最后一步，所有的节点都一个个的单独的节点时候，即排序完成了。