【蓝桥杯】树的重心

树的重心

图的dfs模板

int dfs(int u)
{
    st[u]=true;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(!st[j])
        {
            dfs(j);
        }
    }
}

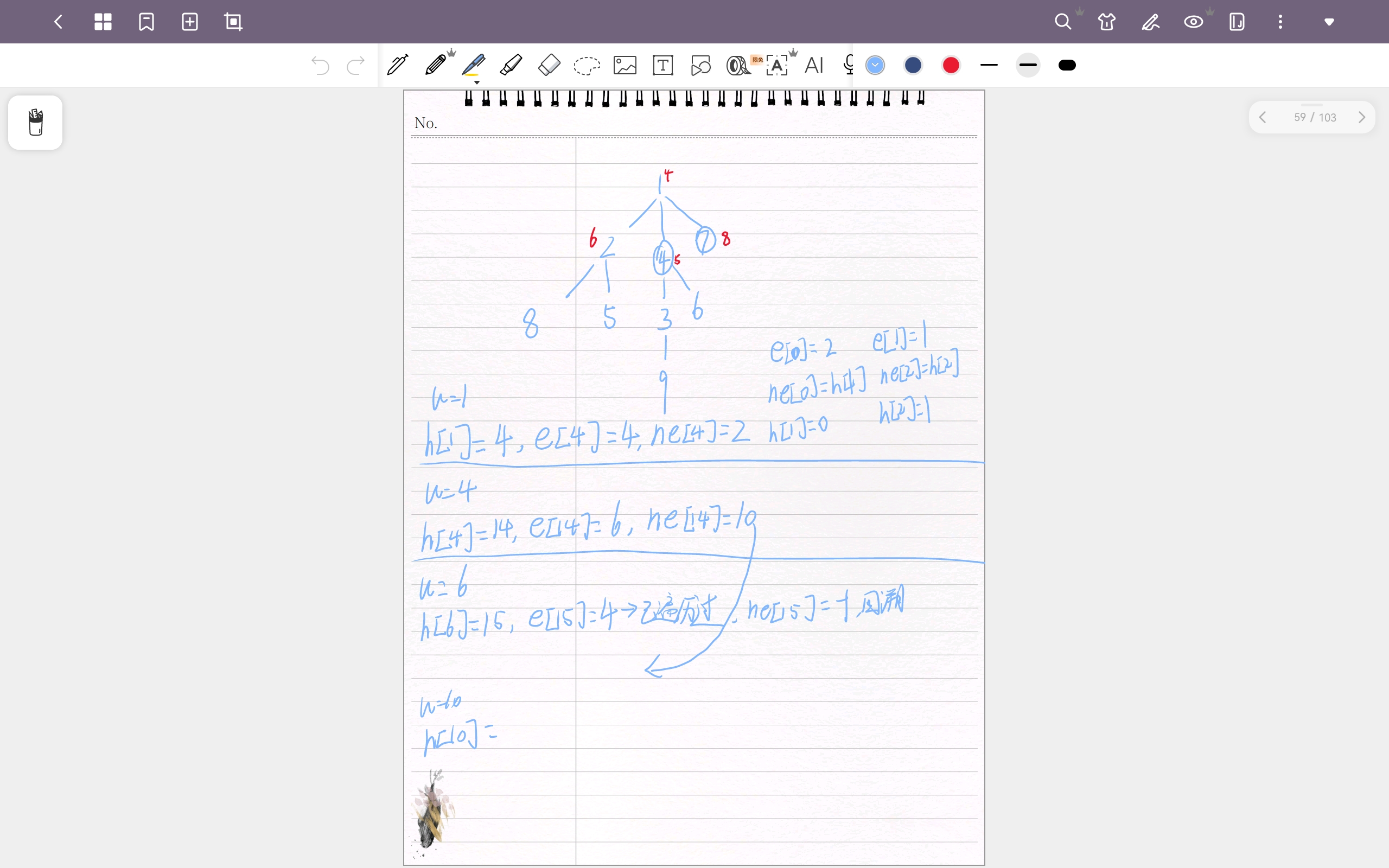
树是这样的。

邻接表：

1: 4->7->2->-1
2: 5->8->1->-1
3: 9->4->-1
4: 6->3->1->-1
5: 2->-1
6: 4->-1
7: 1->-1
8: 2->-1
9: 3->-1

遍历顺序：

4->6->4->3->9->3->4->1->7->1->2->5->2->8->2->1

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
const int N = 100010;
int h[N], e[N * 2], ne[N * 2], d[N], n, m, idx, ans = N;
bool st[N];

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int dfs(int u)
{
    st[u]=true;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        printf("%d->",j);
        if(!st[j])
        {
            dfs(j);
        }
    }
}

int main(void)
{
    memset(h, -1, sizeof(h));
    scanf("%d", &n);
    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        scanf("%d %d", &a, &b);
        add(a, b);
        add(b, a);
    }
    dfs(1);
    
    for(int i=1;i<=n;i++)
    {
        printf("%d: ",i);
        for(int j=h[i];j!=-1;j=ne[j])
        {
            printf("%d->",e[j]);
        }
        printf("-1\n");
    }
    return 0;
}

那么如何来求得树的重心呢？

假设我们以4为重心，那么3和9可以构成一个连通块，6可以构成一个连通块，1、2、5、7、8可以构成一个连通块，这里的最大个数就是5 即->1、2、5、7、8。

这里可以通过遍历每一个节点，假设当前节点是树的重心，来看最大的连通数是多少，然后再找连通数中的最小值。

如果我要知道以2为根的树有多少个节点，我就找2->1也就是u=2，val=1的那一行，因为2指向1表示2已经把它的子树节点收集完毕了，现在要交付于1，也就是以2为根的树的节点数。

如果我要知道以4为根的树有多少个节点就是找4->1，也就是4个节点。

如果我要知道以为3为根的树有多少个节点就是找9->3也就是1个节点。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;

const int N = 100010;
int h[N * 2], e[N * 2], ne[N * 2], n, ans = N, idx;
bool st[N];
void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int dfs(int u)
{
    st[u] = true;
    int sum = 1, res = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int val = e[i];
        //printf("u= %d val= %d  sum= %d \n", u,val, sum);
        if (!st[val])
        {
            int s = dfs(val);
            sum += s;
            res = max(res, s);//最大的子树
        }
        printf("u= %d val= %d  sum= %d \n", u,val, sum);
    }
    res = max(res, n - sum);
    ans = min(ans, res);
    return sum;
}

int main(void)
{
    memset(h, -1,sizeof(h));
    scanf("%d", &n);
    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        scanf("%d %d", &a, &b);
        add(a, b);
        add(b, a);
    }
    dfs(1);
    cout << ans;
    return 0;
}