刷怪日记-二叉树的最近公共祖先

题目

解题思路

• 看见这道题首先应该想到自下向上遍历，最近公共祖先应该先找到p和q，然后再往上找最近公共祖先。

• 回溯就是典型自行向上，而后序遍历就是天然的回溯过程，可以根据左右节点返回值，去处理中节点的值。

• p和q的最近公共祖先有以下2种情况

  1. 情况一：如果找到一个节点，发现其左子树出现p或q，右子树出现p或q(注意：题目给出每个节点都是唯一的)，那么该节点就是p和q的最近公共祖先节点。

     

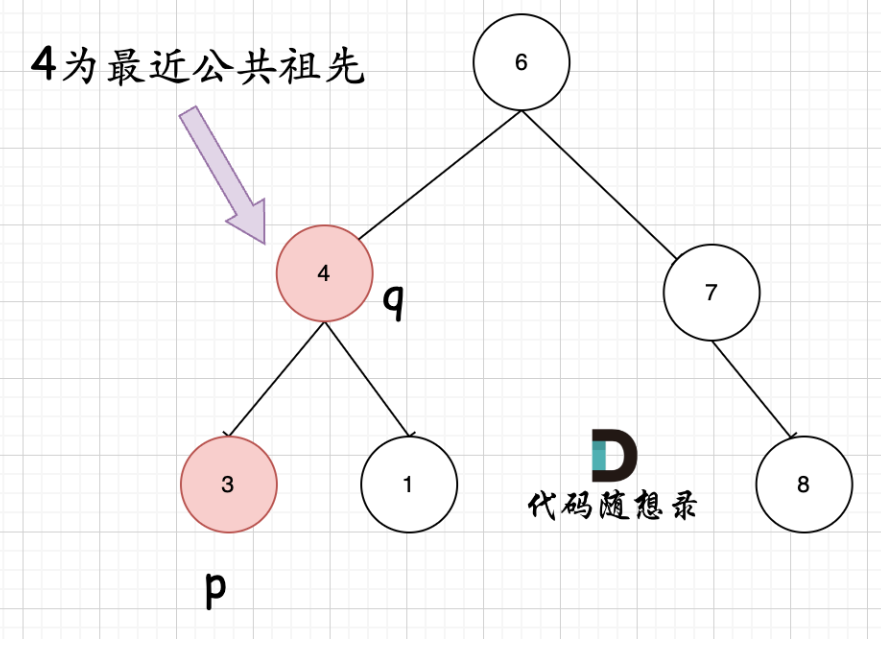
  2. 情况二：节点本身(p或q)拥有一个子节点p或q。

  

• 从一定角度看，情况一和情况实现过程都一样。实现情况一的逻辑顺便包含情况二，因为遇见p或者q都是直接返回，这样也就包含了p或q本身就是公共祖先情况。

• 编写代码时候先确定递归三步曲

  1. 递归函数返回值和参数：基于上述直接返回TreeNode类型值，参数传递TreeNode即可。

  2. 确定终止条件：如果节点为空直接返回空，root == p || root == q时，则直接返回，不需要递归root的子树。

  3. 确定单层递归逻辑：搜索整个树写法如下。注意返回值，仅当节点为空，或者等于p或q，也就仅返回null、p和q。存在以下三种情况。

     left = 递归函数(root->left);  // 左
     right = 递归函数(root->right); // 右
     left与right的逻辑处理;         // 中 
     

     1. 情况一：left == null && right == null表示没找到，直接返回null

     2. 情况二：left != null && right == null 表示root的右子树存在p或q，反之同理。

     3. left != null && right != null 表示 p 和 q分别在root的左右子树，直接返回root。

     4. 注意，p或q本身可能就是最近公共祖先，例如下述情况。因此可能递归到节点4就直接返回了，不进行接下来递归。具体可以对照代码理解。这里不用担心没有找到2会不会不对，因为会遍历整个树，如果其他地方没找到，表明2是4的的子节点。

        

• 补充如何区分一条边，还是搜索整棵树呢

  1. 搜索一条边写法

     if (递归函数(root->left)) return ;
     
     if (递归函数(root->right)) return ;
     

  2. 搜索一棵树写法

     left = 递归函数(root->left);  // 左
     right = 递归函数(root->right); // 右
     left与right的逻辑处理;         // 中 
     

  3. 搜索一条边时候，递归函数返回值不为空的时候，立刻返回，其他节点就不再递归，例如在左子树找到目标情况，便不会递归左子树。搜索一颗树，直接用用left和right分别承接返回值，用于后续处理。

具体代码

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        
        if(root == null || root == p || root == q) return root;

        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left == null && right == null) return null;
        else if(left == null && right != null) return right;
        else if(left != null && right == null) return left;
        else return root;
    }