南京邮电大学《数学实验》模块一（Matlab基础练习）参考答案

一、前提声明

软件支持：MATLAB2020a

软件获取步骤：登录智慧校园——进入左下角“正版软件”——进入后点击“MATLAB”按步骤安装即可，软件较大，请提前规划安装路径和磁盘空间。

1.1?

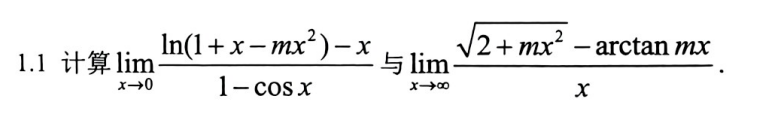
(1)
syms x；
syms m;
m=519;
limit((log(1+x-m*x^2)-x)/(1-cos(x)))

ans=

-1039

(2)
syms x；
syms m;
m=519;
limit((sqrt(2+m*x^2)-atan(m*x))/x,x,inf)

ans=

519^(1/2)

1.2

syms x;
syms y;
syms m;
m=519;
y=exp(m*x)*sin(x);
diff(y,x,2)%求解f（x）的二阶导数

ans =
 
1038*exp(519*x)*cos(x) + 269360*exp(519*x)*sin(x)

subs(diff(y,x,6),x,0)%求解f（x）的六阶导数，再令x等于0

ans =
 
225934558707528

1.3

?

syms x;
int((x+sin(x))/(1+cos(x)),x)%求解不定积分
 
ans =
 
x*tan(x/2)

syms x;
syms m;
m=519;
int((log(1+m*x)-m*x),x,0,1)%求解定积分
 
ans =
 
(520*log(520))/519 - 521/2

1.4

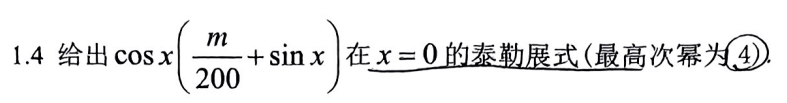
syms x;
syms m;
m=519;
taylor(cos(x)*(m/200+sin(x)),x,'Order',5)
 
ans =
 
(173*x^4)/1600 - (2*x^3)/3 - (519*x^2)/400 + x + 519/200

1.5?

syms m;
m=519;
x(1)=rand(1);
for n=2:10
x(n)=sqrt(m/100+x(n-1))
end;
x


x =

    0.2785    2.3385    2.7438    2.8167    2.8296    2.8319    2.8323    2.8324    2.8324    2.8324

1.6

syms m;
m=519;
A=[4 2 m-2; -3 0 5; 1 5 2*m];
B=[3 4 0; 2 0 -3; -2 1 1];
a=det(A)%计算A的行列式

a =

  -1617

aa=inv(A)%计算A的逆矩阵

aa =

    0.0155   -0.3148   -0.0062
   -1.9289   -2.2480    0.9716
    0.0093    0.0111   -0.0037

[p,d]=eig(A)%p为A的特征向量，d为A的特征值

p =

   -0.4470   -0.7928   -0.1244
   -0.0030    0.6095   -0.9922
   -0.8945   -0.0022    0.0049


d =

   1.0e+03 *

    1.0385         0         0
         0    0.0039         0
         0         0   -0.0004

m=A/B%求解AB-1

m =

   42.1600 -227.8800 -166.6400
    0.0400   -1.7200   -0.1600
   83.9600 -456.2800 -330.8400

n=A\B%求解A-1B

n =

   -0.5708    0.0557    0.9382
  -12.2257   -6.7440    7.7155
    0.0575    0.0334   -0.0371

s=rref([A,B])%求解分块矩阵[A,B]的行最简形

s =

    1.0000         0         0   -0.5708    0.0557    0.9381
         0    1.0000         0  -12.2257   -6.7440    7.7155
         0         0    1.0000    0.0575    0.0334   -0.0371

?1.7

（1）

M文件：?

f.m:

function y=f(x)
if x>=0&&x<=(1/2)
    y=2*x;
elseif x>=(1/2)&&x<=1
    y=2*(1-x);
end

g.m:

function y=g(x,f)
n=length(x);
for i=1:n
    y(i)=f(x(i));
end
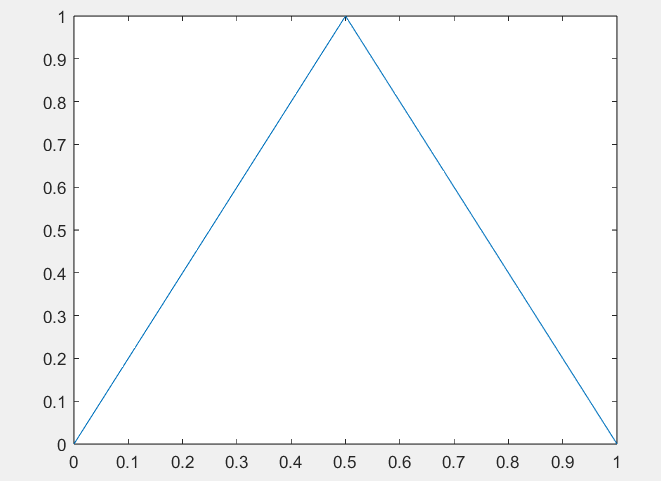
end

画图命令为：

?fplot(@(x)g(x,@f),[0,1])

结果显示为 ：

（2）

M文件：

f.m:

function y=f(x)
if x>=-pi&&x<0
    y=x-1;
elseif x>=0&&x<=pi
    y=x+1;
end

g.m :

function y=g(x,f)
n=length(x);
for i=1:n
    y(i)=f(x(i));
end
end

画图命令为：

fplot(@(x)g(x,@f),[-pi,pi])

结果显示为 ：

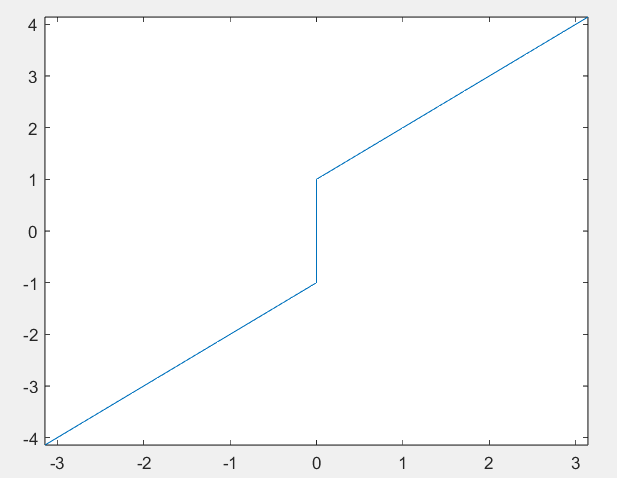
1.8?

(1)

代码为：?

syms x;
syms m;
m=519;
t=-m/100:0.01:m/100;%不同的学号对应的定义域不同，请注意
x=m/20*cos(t);
y=m/20*sin(t);
z=t;
plot3(x,y,z)

?结果显示为：

（2）?

代码为：

syms x;
syms m;
m=519;
t=-m/100:0.01:m/100;%不同的学号对应的定义域不同，请注意
x=cos(t)+t.*sin(t);
y=sin(t)-t.*cos(t);
z=-t;
plot3(x,y,z)

结果显示为：

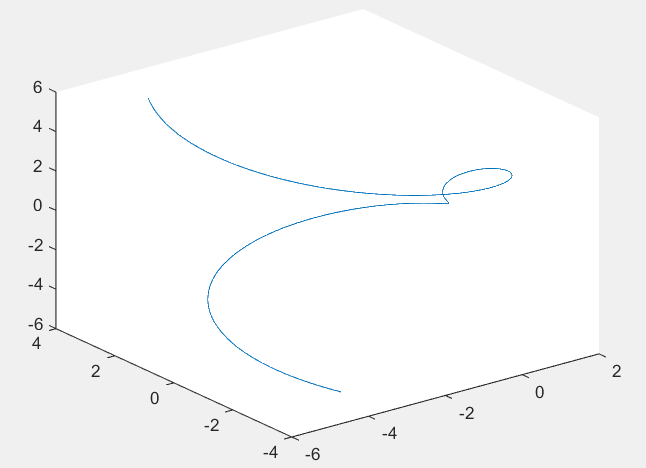
1.9?

代码为：?

syms x;
syms m;
m=519;
a=[1000/m,500/m,100/m];
color=['r','m','g'];%任选三个颜色即可
x=linspace(-10,10);%选取展示区间为[-10,10]
for i=1:3
y=(1/(sqrt(2*pi).*a(i)))*exp(-x.^2/(2*a(i).^2));
plot(x,y,'color',color(i))
hold on
end

显示结果为：

1.10?

代码为?

syms x;
syms y;
ezplot('log(x^2+519*y)-x^3*y-sin(x)')%此处需将自己学号直接代入，若使用m会被ezplot命令当作一个变量

显示结果为：

1.11?

代码为：?

syms x y z m;
m=519;
x = -5: 0.1: 5; y = -5: 0.1: 5;
[x y]=meshgrid(x,y);%将x和y转换为矩阵数据
z= m*x.*exp(-(x.^2+y.^2));
mesh(x,y,z);

显示结果为：

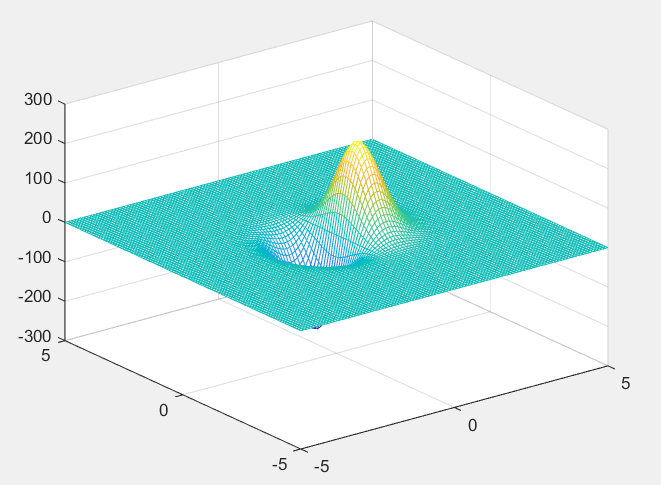
?1.12

（1）

画图代码为：?

syms x;
fplot(@(x)x.^3+sqrt(519)*x.^2+(519/3-3)*x-sqrt(519)*(1-519/27),[-sqrt(519)/3-2,-sqrt(519)/3+2])%此处需将自己学号直接代入，若使用m会被fplot命令当作一个变量
grid on

图形是：

（2） 通过观察图形后用近似求根命令：

fsolve( 'x.^3+sqrt(519)*x.^2+(519/3-3)*x-sqrt(519)*(1-519/27)', -9)

ans =

   -9.3259

fsolve( 'x.^3+sqrt(519)*x.^2+(519/3-3)*x-sqrt(519)*(1-519/27)', -8)

ans =

   -7.5939

fsolve( 'x.^3+sqrt(519)*x.^2+(519/3-3)*x-sqrt(519)*(1-519/27)', -6)

ans =

   -5.8618

即可求解出方程的实根，再对函数进行求导（diff命令）求根（fsolve命令）即可求得导数的实根（原方程的极值点），结合导数的图像即可求解方程的单调区间（此处不再进行代码阐述）。

（3）请结合微积分知识自行阐述。

（4）请自行阐述自己做本题的体会。

持续更新中......敬请期待o.0

》》》》》》如有差错，还请各位小主原谅《《《《《《