【算法每日一练]-数论 （保姆级教程 篇2 ）#行列式 #甜甜花研究 #约数个数 #模数 #数树 #盒子与球

目录

今日知识点：

辗转相减法化下三角求行列式

组合数动态规划打表

约数个数等于质因数的次方+1的乘积

求一个模数

将n个不同的球放入r个不同的盒子：f[i][j]=f[i-1][j-1]+f[i-1][j]*j

行列式?

甜甜花的研究?

约数个数

模数?

数树?

盒子与球?

---

????????

????????

行列式?

给出一个矩阵求 行列式。

输入：??
1
3
1 -2 -1
0 3 2
3 1 -1

思路：

不能直接乘上上面行的倍数来消除本行对应元素。试试辗转相减法把。

(1,3)减去2倍(0,1)->(1,0)

(5,3)减去0倍(3,5)减去1倍(2,3)减去1倍(1,2)减去2倍(0,1)->(1,0)

然后每次检查上面行的元素是否为0，然后换回来就行了

#include <bits/stdc++.h>
using namespace std;
const int mod=0x1f1f1f1f;
typedef long long ll;
ll t,n,a[10][10];
ll solve(){//计算行列式，化简成下三角型（有点类似辗转相除法）
	ll res=1,w=1;//res是结果，w是符号
	for(int i=1;i<=n;i++){//对[i][i]元素所在的列处理
		for(int j=i+1;j<=n;j++){
//我们每次都让下面的行减去上面行的a[j][i]/a[i][i]倍，然后再让最小的行放到上面判断是不是[i][i]是不是0，如果不是就继续。
			while(a[i][i]){
				ll di=a[j][i]/a[i][i];
				for(int k=i;k<=n;k++){
					a[j][k]=(a[j][k]-di*a[i][k]%mod+mod)%mod;//有负数的话要加一次mod
				}
				swap(a[i],a[j]);
				w=-w;
			}
			swap(a[i],a[j]);
			w=-w;
		}
	}
		for(int i=1;i<=n;i++)
			res=a[i][i]*res%mod;
		res=w*res;
		return (res+mod)%mod;	
}

int main(){
	cin>>t;
	while(t--){
		cin>>n;
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
			cin>>a[i][j];
		cout<<solve()<<'\n';
	}	
}

????????

????????

甜甜花的研究?

有n个各不相同的甜甜花种子，现在雇佣了m个人，每人能照顾ai个花。问一共多少种分配方法把花分出去。（数据保证种子有剩余）

输入? ? ? ? ? ?输出：20（结果对12520取模）
5 2
3 1

思路：

因为种子一定有剩余。那么第一个人可以有C(a1,n)种分法，第二个人有C(a2,n)种分法……

乘起来就完事了。主要是数据很大，直接一个个硬算不划算。直接上公式：

C(m,n)=C(m-1,n-1)+C(m-1,n);

记忆：每个人都有两种状态要么是被选到要么未被选到。C(m-1,n-1)对应被选到的情况数，C(m-1,n)对应未被选到的情况数

然后利用动态规划打表就会非常快了。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,num,ans=1;
ll a[10007][107];

int main(){
	cin>>n>>m;
	a[0][0]=1;
	for(int i=1;i<=10000;i++){//利用动态规划求组合数[i][j]=[i-1][j-1]+[i-1][j]
		a[i][0]=1;
		for(int j=1;j<=100;j++){
			a[i][j]=(a[i-1][j-1]+a[i-1][j])%12520;
		}
	}
	for(int i=1;i<=m;i++){
		cin>>num;
		ans=ans*a[n][num]%12520;
		n-=num;
	}
	cout<<ans;
}

??????

????????

约数个数

求n的约数个数。

#include <bits/stdc++.h>
using namespace std;
int main(){方法一：直接找就完了，约数一定成对出现，但是相等时候要特判一下
	int n,ans=0;cin>>n;
	for(int i=1;i*i<=n;i++){
		if(n%i==0)ans+=2;
		if(i*i==n)ans--;
	}
	cout<<ans;
}
//
//int main(){ //方法二：约数等于质因数的次方加1的乘积
//	int n,ans=1;cin>>n;
//	for(int i=2;i*i<=n;i++){
//		int tmp=0;
//		while(n%i==0){
//			tmp++;n/=i;//求质因数的次数
//		}
//		ans*=(tmp+1);
//	}
//	if(n!=1)ans*=2;//最后的质因数也不要忘了
//	cout<<ans;
//}

???????????

????????

模数?

输入a，b问有多少个x使得a%x==b。如果有无穷多个输出infinity，不存在输出0。

思路：

首先分析一下，a%x==b，等价于找a-b的因数（约数）个数。但是先等等：这个因数还必须满足比余数大。

#include <bits/stdc++.h>
using namespace std;

int run(int a,int b){
	int ans=1;
	for(int i=2;i*i<=a;i++){
		if(i<=b||a/i<=b)continue;
		int tmp=0;
		while(a%i==0){//判断是不是质因数
			tmp++;a/=i;//一边缩小a
		}
		ans*=(tmp+1);
	}
	if(a!=1)ans*=2;
	return ans;
}

int main(){
	int a,b;
	cin>>a>>b;
	if(a==b){
		cout<<"infinity";
		return 0;	
	}
	if(a<b){
		cout<<0;return 0;
	}
	cout<<run(a-b,b);
	
}

?????????

????????

数树?

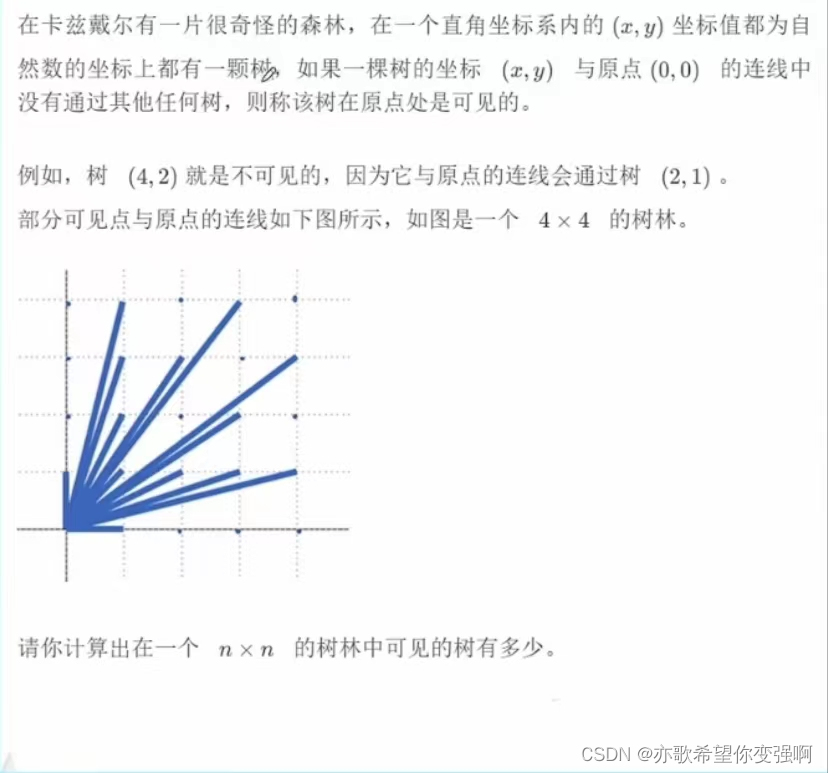
思路：

反正就是不能出现其他组的倍数这种情况。?可以直接上筛子，提前把不成立给筛掉，不过有点麻烦。

仔细观察不难你会发现：

只要（a，b）的最大公约数不是1，那么就一定不是答案。然后统计就行了

#include <bits/stdc++.h>
using namespace std;
int c,n;

int gcd(int a,int b){//辗转相除法(36,14)(14,8)(8,6)(6,2)(2,0)->2
	return b==0?a:gcd(b,a%b);//(25,14)(14,11)(11,3)(3,2)(2,1)(1,0)->1
}

int main(){
	cin>>c;
	for(int i=1;i<=c;i++){
		cin>>n;
		int ans=0;
		for(int j=1;j<=n;j++)
			for(int k=1;k<=n;k++){
				if(gcd(j,k)==1)ans++;
			}
		cout<<i<<" "<<n<<" "<<ans+2<<'\n';
	}
}
/*
4
2
4
5
231
*/

????????

?????????

盒子与球?

现有r个互不相同的盒子和n个互不相同的球，要将这n个球放入r个盒子中，且不允许有空盒子，一共有多少种放法？

思路：

主要是状态转移式子。f[i][j]=f[i-1][j-1]+f[i-1][j]*j;

我们设置f[i][j]表示i个球j个盒子的放法。那么对于第i个球，要么自己一个盒子f[i-1][j-1]情况数，要么和别人一个盒子但是有j中选择f[i-1][j]*j种情况数。不断递推就行了

#include <bits/stdc++.h>
using namespace std;
int n,r,f[20][20],ans;

int main(){
	cin>>n>>r;
	f[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=min(i,r);j++){
			f[i][j]=f[i-1][j-1]+f[i-1][j]*j;
		}
	}
	ans=f[n][r];
	for(int i=1;i<=r;i++){
		ans*=i;
	}
	cout<<ans;
}
/*
3 2
6*/