DFS && BFS

用DFS和BFS分别实现

//这边给出DFS的模版
void dfs(int x,int y)
{
	//判断是否到达终点（只有给出结束点的时候需要） 
	if (x == ex && y == ey) {
        if (min_steps > step) {
            min_steps = step;
        }
        return;
    }
	//给出移动方向
	int move[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
	//以当前的点为基础，开始搜索，搜索的路线为右遇到障碍物或者边界变成向下...... 
	for (int i = 0; i < 4; ++i) {
        int tx = x + move[i][0], ty = y + move[i][1];
        if (tx < 0 || tx >= m || ty < 0 || ty >= n) continue;
        if (a[tx][ty] == 0 && v[tx][ty] == 0) {
            v[tx][ty] = 1;//走过的点打上标记，防止再走一遍 
            dfs(tx, ty, step + 1);
            v[tx][ty] = 0;//由于回溯的需要，需要接触标记，找下一条路径 
        }
    }
    return;	
} 

以下是完整的DFS代码

#include<bits/stdc++.h>
#define itn int
using namespace std;
int sx, sy, ex, ey;
int min_steps = 1000000;
int a[100][100];
int v[100][100];
int m, n;
void dfs(int x, int y, int step) {
    int move[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    if (x == ex && y == ey) {
        if (min_steps > step) {
            min_steps = step;
        }
        return;
    }
    for (int i = 0; i < 4; ++i) {
        int tx = x + move[i][0], ty = y + move[i][1];
        if (tx < 0 || tx >= m || ty < 0 || ty >= n) continue;
        if (a[tx][ty] == 0 && v[tx][ty] == 0) {
            v[tx][ty] = 1;
            dfs(tx, ty, step + 1);
            v[tx][ty] = 0;
        }
    }
    return;
}
int main() {
    cin >> sx >> sy >> ex >> ey;
    cin >> m >> n;
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            cin >> a[i][j];
        }
    }
    v[sx][sy] = 1; 
    dfs(sx, sy, 0);  
    cout << "Minimum steps needed: " << min_steps << endl;
    return 0;
}

? BFS部分：

#include<bits/stdc++.h>
#define itn int
using namespace std;
struct Queue{
	int x;
	int y;
	int s;
};
int a[50][50];
int vis[50][50];
int main()
{
	struct Queue queue[2501];
	int sx,sy,ex,ey,n;
	int flag=0;
	cin>>sx>>sy>>ex>>ey>>n;
	for (int i=0;i<n;++i)
	{
		for (int j=0;j<n;++j)
		{
			cin>>a[i][j];
		}
	}
	int tail=0,head=0;
	queue[tail].x=sx,queue[tail].y=sy,queue[tail].s=0;
	int move[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
	while (head!=tail)
	{
		int x=queue[head].x,y=queue[head].y;
		for (int i=0;i<=3;++i)
		{
			int tx=x+move[i][0],ty=y+move[i][1];
			if (tx==ex && ty==ey)
			{
				flag=1;
				break;
			}
			if (tx<0 || tx>=n || ty<0 || ty<=n) continue;
			if (a[tx][ty]==0 && vis[tx][ty]==0)
			{
				vis[tx][ty]=1;
				queue[tail].x=tx;
				queue[tail].y=ty;
				queue[tail].s=queue[head].s+1;
				tail++;
			}
		}
		if (flag)break;
		head++;
	}
	cout<<queue[tail-1].s;
}

最大岛屿面积https://leetcode.cn/problems/max-area-of-island/description/

给你一个大小为?m x n?的二进制矩阵?grid?。

岛屿?是由一些相邻的?1?(代表土地) 构成的组合，这里的「相邻」要求两个?1?必须在?水平或者竖直的四个方向上?相邻。你可以假设?grid?的四个边缘都被?0（代表水）包围着。

岛屿的面积是岛上值为?1?的单元格的数目。

计算并返回?grid?中最大的岛屿面积。如果没有岛屿，则返回面积为?0?。

示例 1：

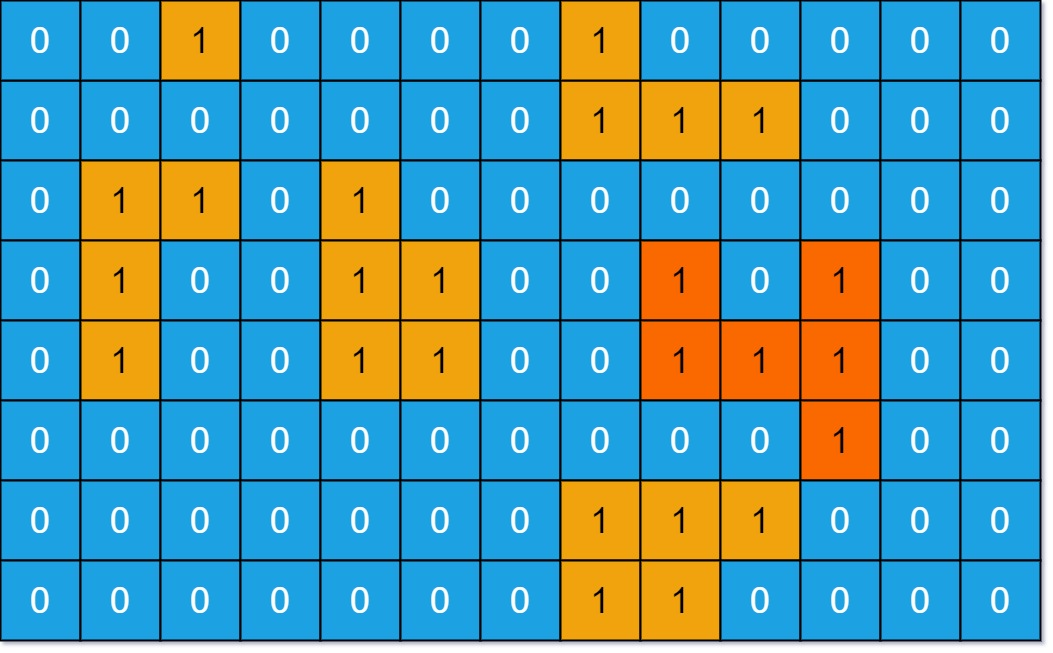
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j]?为?0?或?1

思路：套用搜索模版，找最大的岛屿的面积，只需要便利每一个岛的面积，然后定义一个最大值变量记录最大值就可以。

//BFS
struct Queue{
    int x;
    int y;
};
int vis[55][55];
int maxAreaOfIsland(int** grid, int gridSize, int* gridColSize) {
    struct Queue queue[1000000];
    int line=gridSize;
    int col=*gridColSize;
    int head=0,tail=0;
    int max=0;
    for (int i=0;i<line;++i)
    {
        for (int j=0;j<col;++j)
        {
            if (grid[i][j]==1)
            {
                queue[tail].x=i;
                queue[tail].y=j;
                tail++;
                vis[i][j]=1;
                int sum=1;
                int move[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
                while (head!=tail)
                {
                    int x=queue[head].x,y=queue[head].y;
                    for (int k=0;k<=3;++k)
                    {
                        int tx=x+move[k][0],ty=y+move[k][1];
                        if (tx<0 || tx>=line || ty<0 || ty>=col)continue;
                        if (grid[tx][ty]==1 && vis[tx][ty]==0)
                        {
                            vis[tx][ty]=1;
                            sum++;
                            queue[tail].x=tx;
                            queue[tail].y=ty;
                            tail++;
                        }
                    }
                    head++;
                }
                if (max<sum)max=sum;
            }   
        }
    }
    memset(vis, 0, sizeof(vis));
    return max;
}

//DFS
int line ,col;
int  dfs(int ** grid,int i,int j)
{
    if (i<0 || j>=col || i>=line || j<0 || grid[i][j]==0) return 0 ;
    grid[i][j]=0;
    return 1+dfs(grid,i+1,j)+dfs(grid,i-1,j)+dfs(grid,i,j+1)+dfs(grid,i,j-1);
}
int maxAreaOfIsland(int** grid, int gridSize, int* gridColSize) {
    line=gridSize;
    col=*gridColSize;
    int max=0;
    for (int i=0;i<line;++i)
    {
        for (int j=0;j<col;++j)
        {
            if (grid[i][j]==1)
            {
                int sum=dfs(grid,i,j);
                if (sum>max)max=sum;
            }
        }
    }
    return max;
}

填涂颜色https://www.luogu.com.cn/problem/P1162

题目描述

由数字?00?组成的方阵中，有一任意形状的由数字?11?构成的闭合圈。现要求把闭合圈内的所有空间都填写成?22。例如：6×66×6?的方阵（�=6n=6），涂色前和涂色后的方阵如下：

如果从某个?00?出发，只向上下左右?44?个方向移动且仅经过其他?00?的情况下，无法到达方阵的边界，就认为这个?00?在闭合圈内。闭合圈不一定是环形的，可以是任意形状，但保证闭合圈内的?00?是连通的（两两之间可以相互到达）。

0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 1 0 1
1 1 1 1 1 1

0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 1 2 1
1 1 1 1 1 1

输入格式

每组测试数据第一行一个整数?�(1≤�≤30)n(1≤n≤30)。

接下来?�n?行，由?00?和?11?组成的?�×�n×n?的方阵。

方阵内只有一个闭合圈，圈内至少有一个?00。

输出格式

已经填好数字?22?的完整方阵。

输入输出样例

输入 #1复制

6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1

输出 #1复制

0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1

说明/提示

对于?100%100%?的数据，1≤�≤301≤n≤30。

思路：把1看作墙，遇到就停止搜索下去，但是要注意边界的情况，从边界开始搜索，那么剩下的0的是要变成2的。

#include<bits/stdc++.h>
using namespace std;
int a[35][35],b[35][35];
int n;
void dfs(int x, int y)
{
	int move[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
	for (int i=0;i<=3;++i)
	{
		int tx=x+move[i][0],ty=y+move[i][1];
		if (tx<0 || tx>=n || ty<0 ||ty>=n)continue;
		if (a[tx][ty]==0 && b[tx][ty]==0)
		{
			b[tx][ty]=1;
			dfs(tx,ty);
		}
	}
	return ;
}
int main()
{
	cin>>n;
	for (int i=0;i<n;++i)
	{
		for (int j=0;j<n;++j)
		{
			cin>>a[i][j];
		}
	}
	for (int i=0;i<n;++i)
	{
		if (a[i][0]==0)dfs(i,0);
		if (a[0][i]==0)dfs(0,i);
		if (a[i][n-1]==0)dfs(i,n-1);
		if (a[n-1][i]==0)dfs(n-1,i);
	}
	for (int i=0;i<n;++i)
	{
		for (int j=0;j<n;++j)
		{
			if (b[i][j]==0 && a[i][j]==0)
			{
				a[i][j]=2;
			}
		}
	}
	for (int i=0;i<n;++i)
	{
		for (int j=0;j<n;++j)
		{
			cout<<a[i][j]<<" ";
		}
		cout<<endl;
	}
	return 0;
}

自然数的拆分问题https://www.luogu.com.cn/problem/P2404

题目描述

任何一个大于?11?的自然数?�n，总可以拆分成若干个小于?�n?的自然数之和。现在给你一个自然数?�n，要求你求出?�n?的拆分成一些数字的和。每个拆分后的序列中的数字从小到大排序。然后你需要输出这些序列，其中字典序小的序列需要优先输出。

输入格式

输入：待拆分的自然数?�n。

输出格式

输出：若干数的加法式子。

输入输出样例

输入 #1复制

7

输出 #1复制

1+1+1+1+1+1+1
1+1+1+1+1+2
1+1+1+1+3
1+1+1+2+2
1+1+1+4
1+1+2+3
1+1+5
1+2+2+2
1+2+4
1+3+3
1+6
2+2+3
2+5
3+4

说明/提示

数据保证，2≤�≤82≤n≤8。

思路：主要掌握回溯的用法

#include<bits/stdc++.h>
using namespace std;
int a[35];
int n;
void dfs(int sum, int len, int last) {
    if (sum == n &&len!=1) {
        for (int j = 0; j < len - 1; ++j) {
            cout << a[j] << "+";
        }
        cout << a[len - 1] << endl;
        return;
    }
    for (int i = last; i <= n - sum; ++i) {
        a[len] = i;
        dfs(sum + i, len + 1, i); 
    }
}

int main() {
    cin >> n;
    dfs(0, 0, 1);
    return 0;
}