代码随想录算法训练营29期|day 24 任务以及具体安排

理论基础

#什么是回溯法

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。

在二叉树系列中，我们已经不止一次，提到了回溯，例如二叉树：以为使用了递归，其实还隐藏着回溯?(opens new window)。

回溯是递归的副产品，只要有递归就会有回溯。

所以以下讲解中，回溯函数也就是递归函数，指的都是一个函数。

#回溯法的效率

回溯法的性能如何呢，这里要和大家说清楚了，虽然回溯法很难，很不好理解，但是回溯法并不是什么高效的算法。

因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

那么既然回溯法并不高效为什么还要用它呢？

因为没得选，一些问题能暴力搜出来就不错了，撑死了再剪枝一下，还没有更高效的解法。

此时大家应该好奇了，都什么问题，这么牛逼，只能暴力搜索。

#回溯法解决的问题

回溯法，一般可以解决如下几种问题：

相信大家看着这些之后会发现，每个问题，都不简单！

另外，会有一些同学可能分不清什么是组合，什么是排列？

组合是不强调元素顺序的，排列是强调元素顺序。

例如：{1, 2} 和 {2, 1} 在组合上，就是一个集合，因为不强调顺序，而要是排列的话，{1, 2} 和 {2, 1} 就是两个集合了。

记住组合无序，排列有序，就可以了。

#如何理解回溯法

回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

这块可能初学者还不太理解，后面的回溯算法解决的所有题目中，我都会强调这一点并画图举相应的例子，现在有一个印象就行。

#回溯法模板

这里给出Carl总结的回溯算法模板。

在讲二叉树的递归?(opens new window)中我们说了递归三部曲，这里我再给大家列出回溯三部曲。

在回溯算法中，我的习惯是函数起名字为backtracking，这个起名大家随意。

回溯算法中函数返回值一般为void。

再来看一下参数，因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。

但后面的回溯题目的讲解中，为了方便大家理解，我在一开始就帮大家把参数确定下来。

回溯函数伪代码如下：

void backtracking(参数)

既然是树形结构，那么我们在讲解二叉树的递归?(opens new window)的时候，就知道遍历树形结构一定要有终止条件。

所以回溯也有要终止条件。

什么时候达到了终止条件，树中就可以看出，一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

所以回溯函数终止条件伪代码如下：

if (终止条件) {
    存放结果;
    return;
}

在上面我们提到了，回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

如图：

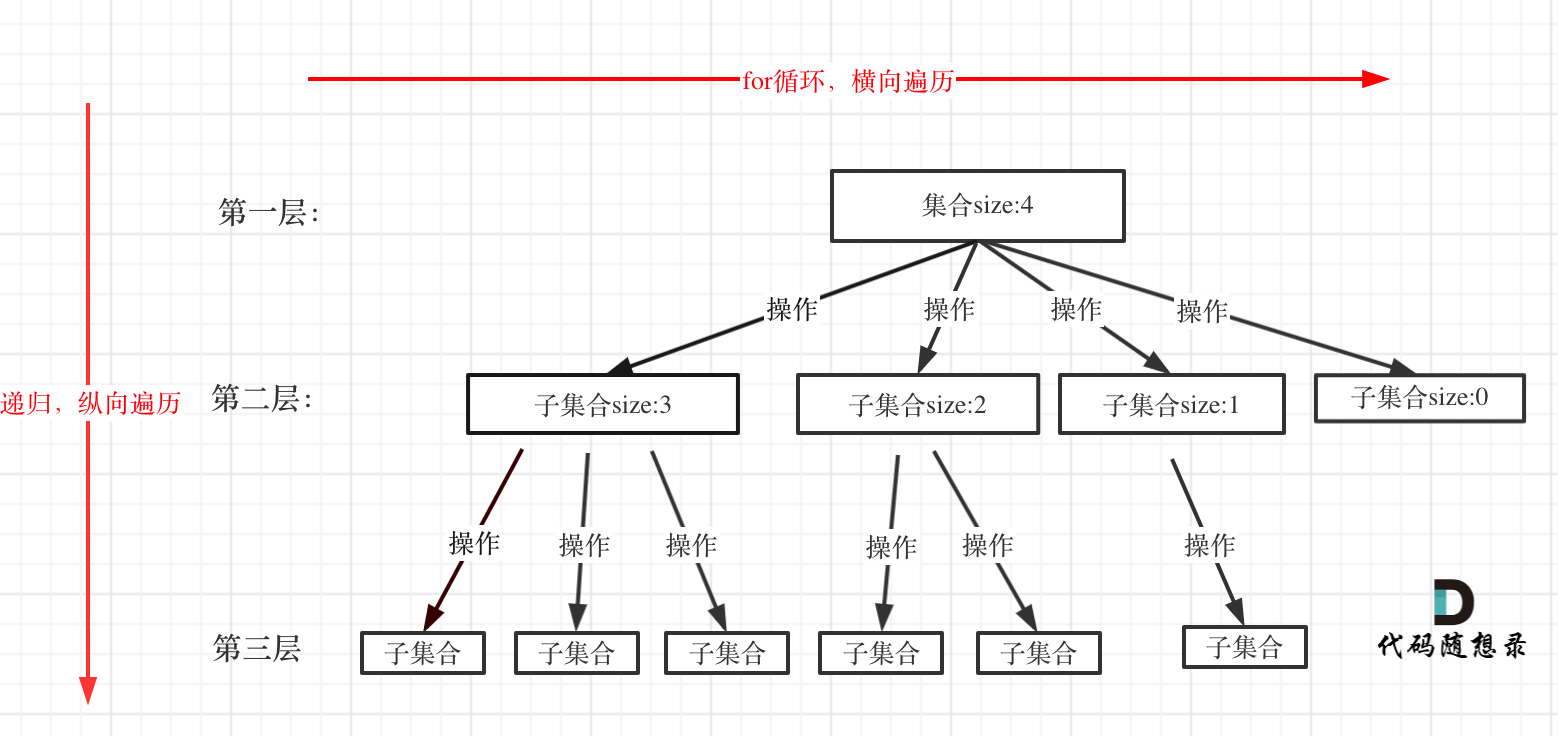
注意图中，我特意举例集合大小和孩子的数量是相等的！

回溯函数遍历过程伪代码如下：

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

backtracking这里自己调用自己，实现递归。

大家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

分析完过程，回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

这份模板很重要，后面做回溯法的题目都靠它了！

如果从来没有学过回溯算法的录友们，看到这里会有点懵，后面开始讲解具体题目的时候就会好一些了，已经做过回溯法题目的录友，看到这里应该会感同身受了。

class Solution {
    List<List<Integer>> result= new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }

    public void backtracking(int n,int k,int startIndex){
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i =startIndex;i<=n;i++){
            path.add(i);
            backtracking(n,k,i+1);
            path.removeLast();
        }
    }
}

思路：关键是回溯，在每一轮中，先path.add(i)再path.removeLast(),实现回溯