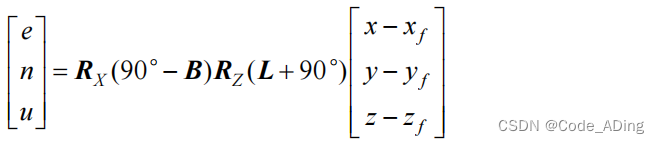测站坐标系统 -- 东北天(ENU)坐标系、站心坐标系
发布时间:2023年12月19日
目录
一、测站坐标系的定义
-
测站坐标系统以观测站( 或地面上某一个观测点 ) 为中心建立坐标系统,将这类坐标系称为测站坐标系统。
-
测站坐标系通常 以用户所在的位置点 P 为坐标原点, 三个坐标轴分别是相互垂直的 东向、 北向和 天向,因而测站坐标系又称为 东北天(ENU)坐标系。 由于测站坐标系以站心为坐标原点,因此也称为站心坐标系。
-
如图所示, 测站坐标系的天向与大地坐标系(LLA经纬度坐标系)在此点的高程方向一致。测站坐标系固定在地球上, 本质上是一种 地固坐标系。

-
(1) 以站心为坐标原点。
-
(2) Z 轴与站心点的椭球法线重合,向上为正(或称为天顶方向) 。
-
(3) X 轴为站心点的正东向。
-
(4) Y 轴为站心点的正北向。
-
二、测站坐标系与地心地固坐标系的转换
- 由测站坐标系的定义可知,测站坐标系与地心地固坐标系的坐标原点不重合,坐标轴指向也不一致。因此,地心地固坐标系与测站坐标系之间的转换涉及两种变换:坐标原点平移和坐标轴旋转。
2.1地心地固坐标系转到测站坐标系
已知测站 F?在地心地固坐标系中的坐标为(xf ,?yf ,zf) ,某一待转换点 S?在地心地固坐标系中的坐标为(x,y, z)?,将待转换点S 由地心地固坐标系转换到测站 F 的测站坐标系具体步骤如下:
- ?(1) 坐标原点平移(两个的enu(测站F和待转换点S)其实是一样的)。将坐标原点由地心平移到站心,得到平移后的坐标(x' , y' , z')。通过
-
(2) 计算测站的大地坐标。将测站的地心直角坐标(x f ,? yf ,zf) 转换为大地坐标(B,L,H)
-
-
(3)计算坐标旋转矩阵。由测站的经度、纬度计算得到坐标旋转矩阵为
-
-
(4) 坐标轴旋转。利用旋转矩阵,将平移后的坐标( x′?,?y' , z′ ) 转到测站坐标系,得到测站坐标系下的位置坐标(e,n,u) 。
-
???????

-
-
综上所述,可以将上述过程合成一个公式,即
-
-
???????

?????????????????????
2.2测站坐标系转到地心地固坐标系
- 已知测站 F 在地心地固坐标系中的坐标为(xf ,?yf ,zf) ,某一待转换点 S 在测站坐标系中的坐标为(e,n ,u ),则将 S 由测站坐标系转换到地心地固坐标系的具体步骤如下:
- (1)计算测站的大地坐标。将测站的地心直角坐标(xf ,?yf ,zf) 转换为大地坐标(B,L ,H)。前面有讲,这里不再赘述
- (2) 计算坐标旋转矩阵。由于从测站坐标系转换到地心地固坐标系是从地心地固坐标系转换到测站坐标系的逆过程
- ???????

- 由于旋转矩阵是正交对称矩阵,其逆矩阵等于矩阵的转置,因此,有?????????????????????
- ??????????????

- ???????
-
(3) 坐标轴旋转。利用旋转矩阵,将测站坐标 ( e,n,u)?旋转到坐标轴与地心地固坐标系一致的坐标( x′?,?y' ,?z′ )
-
???????

-
-
(4) 坐标原点平移。将坐标 ( x′, ,y' ,z ′) 的原点平移至地心,得到转换点 S 在地心地固坐标系中的坐标(x , y ,z)
-
 ???????
???????
-
-
同样地,也可以将上述过程合成一个公式,即:
-
???????
 ????????????????????????????
???????
???????
???????
????????????????????????????
???????
???????
???????
-
三、方位角和高度角的计算
- 测站坐标系的一个重要应用在于计算卫星在用户(观测者)处的观测矢量,进而得到卫星相对于用户的方位角和高度角(也称为仰角)。
- 高度角可用于判断卫星是否对用户可见:高度角小于 0°,说明卫星位于地平线以下,不可见;反之,高度角大于 0°时,卫星可见。高度角等于 90°时,表示卫星位于用户的天顶正上方。
-
假设卫星在测站坐标系中的坐标为(e,n,u ) ,则卫星高度角的计算公式为
-
???????

-
-
卫星方位角定位为由北向顺时针转到观测矢量在水平面内的投影方向上的角度,其 计算公式为:
-
-

???????
文章来源:https://blog.csdn.net/qq_43381998/article/details/135094068
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 第27章 对于复数矩阵的进一步理解,前两章看不懂就看看这个
- ESP32 - MicroPython WiFi和热点的使用
- openssl3.2 - 官方demo学习 - cipher - aesgcm.c
- Android开发中使用Coil
- 23种设计模式【创建型模式】详细介绍之【原型模式】
- 防勒索病毒攻击的关键措施
- BGP防环机制介绍
- 服务熔断(Hystrix)
- 【JVM】垃圾回收 GC
- 数字孪生技术助力澳大利亚绿色能源行业