《数据结构》实验报告-实验三 树形结构及其应用

《数据结构》实验报告-实验三 树形结构及其应用

一、问题分析

（1）任务1中，需要根据带“#”的先序序列构造一棵二叉树（“#”表示空，可以唯一确定一棵二叉树），因为输入的先序序列，总是先构造出根节点，然后再到左孩子，最后才是右孩子，这种重复的模式可以用递归来降低模拟难度，提高程序可读性。之后要求输出新建二叉树的前序序列（不带“#”），中序序列和后序序列，均可以用递归来实现，只是访问根节点、左孩子和右孩子的顺序不一样。只要处理好递归的逻辑，不出现无限递归，问题就可以很快被解决。
（2）任务2中，根据给定的二叉树的后序遍历序列和中序遍历序列，构造该二叉树，并输出该二叉树的先序遍历。这是本次实验的重难点。首先要清楚后序序列和中序序列的性质，再通过模拟和递归构建起一颗新的二叉树。主要利用了后序序列最后一个结点就是根节点的性质，将中序序列划分为左子树和右子树的中序序列，再根据根节点在中序序列的坐标将后序序列也划分为左子树和右子树的后序序列，以上过程重复递归即可。在划分过程中要注意下标的问题，必须清楚的知道现在要划分的区间长度，起点和终点。在模拟过程中还会出现无法构造该树的情况，也要进行特殊判断。
（3）任务3中，要求统计任务2中构造的二叉树的叶子结点数和二叉树的宽度。因为叶子结点在二叉树的最低端，且要遍历所有叶子结点，计算机需要进行深度优先搜索来找到他们。如果在搜索时顺便统计每一层的结点数，最后取最大值为宽度，就不用遍历两次二叉树了。每到一个结点就根据它的层数使统计数组增一。同样是通过递归来搜索。
（4）任务4中，需要判断任务1和任务2中构造的数是否等价。只要有一个结点不一样，就要输出0。可以按照先序遍历和递归的方法检查每一个结点，当发现不一致时就逐级返回，要增加对空的判断。
总而言之，在构造和解析二叉树的过程中，最重要的就是利用递归的复用性，将大问题拆分成相同模式的小任务，让程序递归执行小任务便可以得到最终结果。还要注意判断返回的条件和模拟的小细节，递归时程序更容易出现异常。

二、详细设计

2.1设计思想

（1）任务1主要利用了递归建立二叉树的思想。输入要建立二叉树的带“#”的先序序列，逐一获取序列的字符来构造当前的根节点（相对于子树），然后递归调用该方法建立左孩子的子树，同样会以左孩子为其子树的根节点，右孩子类似。在遇到“#”后，说明该节点是空的，要做特殊判断并返回空给它的根节点，表明该结点无此孩子。建立好二叉树后，要依次进行三种遍历。我均采用了递归遍历的方法，只是遍历的顺序不一样。在先序遍历时，先访问根节点，在以先序遍历左孩子，返回后再先序遍历右孩子，这样在以孩子为根节点的下一层递归中，又可以重复此过程。当孩子为空时，直接返回即可。中序和后序遍历类似，仅仅调换了访问和遍历的顺序。这样就可以完成一棵二叉树的构建和遍历了。
（2）任务2中，首先要判断输入的后序和中序序列长度是否一致，不一致直接返回并提示不能构造的信息。然后进入逻辑较为复杂的从后序和中序序列中以还原出先序序列，并按照该先序序列的顺序建立二叉树的函数中。该函数要获取后序序列和中序序列的字符串，还有这两个序列的起止坐标。根据后序序列的性质，其末尾对应的结点就是根节点，又因为在中序序列中，根节点位置两边的序列就是其左右子树的中序序列。接着根据左右子树的中序序列位置和长度，进一步划分后序序列为左子树的后序序列和右子树的后序序列。然后递归调用该函数，并先后传入左右子树的中序和后序序列和起止坐标。当后序和先序序列被细分到只含一个元素时，说明该元素对应二叉树的叶子结点，做特殊判断后返回即可。这样就可以以先序顺序来构建一颗二叉树。在中序序列找根节点时，可能会出现寻找失败的情况，这时就说明给出的后序和先序序列是无法构建一颗二叉树的，要返回错误。最后采用任务中先序遍历的方法遍历二叉树即可。
（3）任务3中，需要统计任务2中构建的二叉树的叶子节点数和宽度。这需要将二叉树完全遍历一遍，我利用了先序遍历也就是深度优先搜索一种思想的，每次搜索都搜索到叶子结点才返回，并不进行逐层遍历。但是因为要同时统计每层的结点数，需要事先构造一个位于全局变量位置的深度统计数组，存储每深度的结点数，并在搜索函数中传入当前结点的深度值，根据深度值往对应数组中增一即可。同时还需要一个记录二叉树高度的全局变量，在统计完所有叶子结点后，取达到过的最大深度为高度，再扫过一次统计数组便可找出最大值，即二叉树的宽度。
（4）任务4中，要判断任务1和任务2中构造的二叉树是否等价。这同样需要递归判断每一个结点的数值和位置是否一致。遍历时仍采用先序遍历的方法，先判断根节点是否相同，再先后判断左子树和右子树是否相同，在子树中继续进行递归判断。任何一个结点不同就要逐层返回不等价的信息。还要注意判断结点为空的情况，这时要求两颗二叉树的当前结点同时为空，否则仍然要返回不等价的信息。如果所有节点都返回正确，则输出1。
因为任务3和任务4中会用到任务1和任务2构造的新二叉树，如果构造不成功，将不能继续进行任务3和任务4。所以当任务2中出现不能构造新二叉树的情况时，直接弹出提示并终止程序。这样可以在顺序指向任务时及时掐断构造失败的树，防止执行相关任务时出现异常。

2.2 存储结构及操作

2.2.1存储结构
实验中采用二叉链表的方式构造二叉树，二叉树结点Node的结构体包含内容有：
Char类型变量data，存储二叉树结点的数据。
Node类型指针变量lchild和rchild，分别指向左孩子和右孩子结点。
同时定义该结构体的指针类型为BiTree。

2.2.2 涉及的操作
实验1中的栈相关函数，如表1所示。

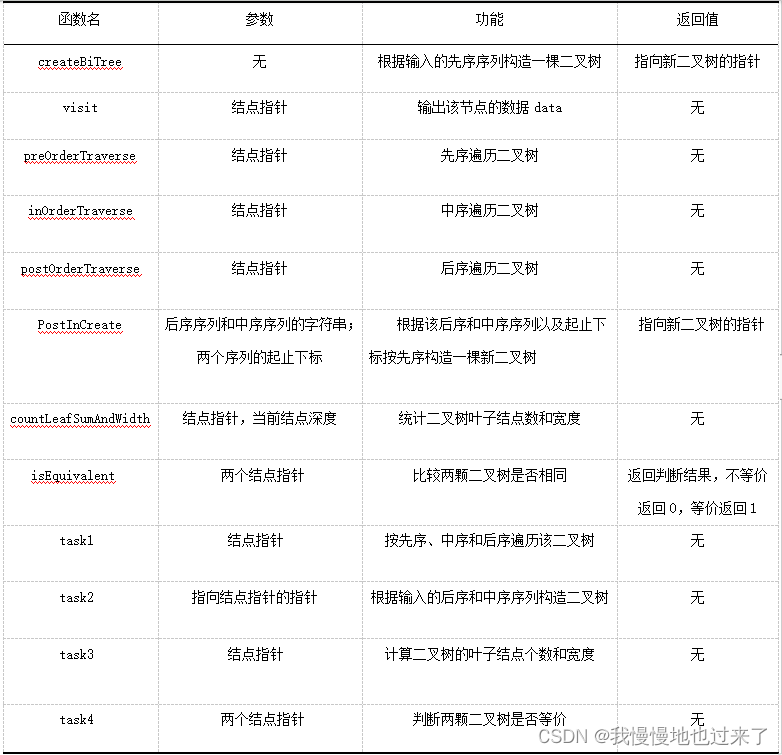
表1

2.3 程序整体流程

（1）实验整体流程图如图1所示。

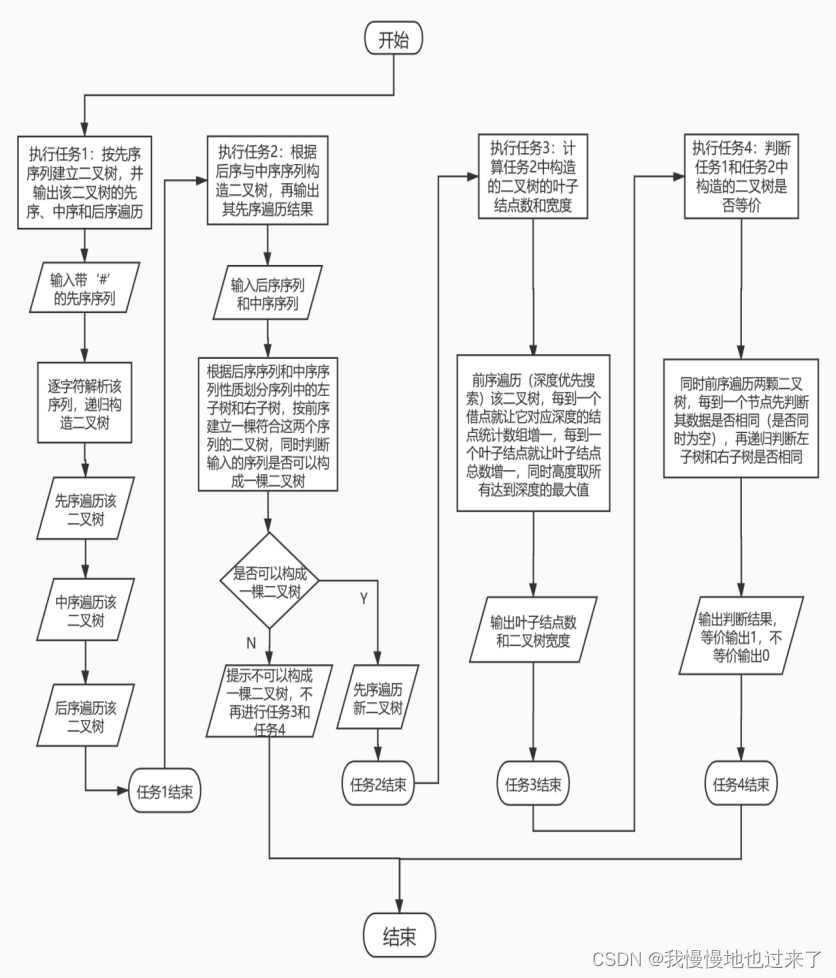
图 1
（2）任务1按先序序列构建二叉树算法流程图，如图2所示。

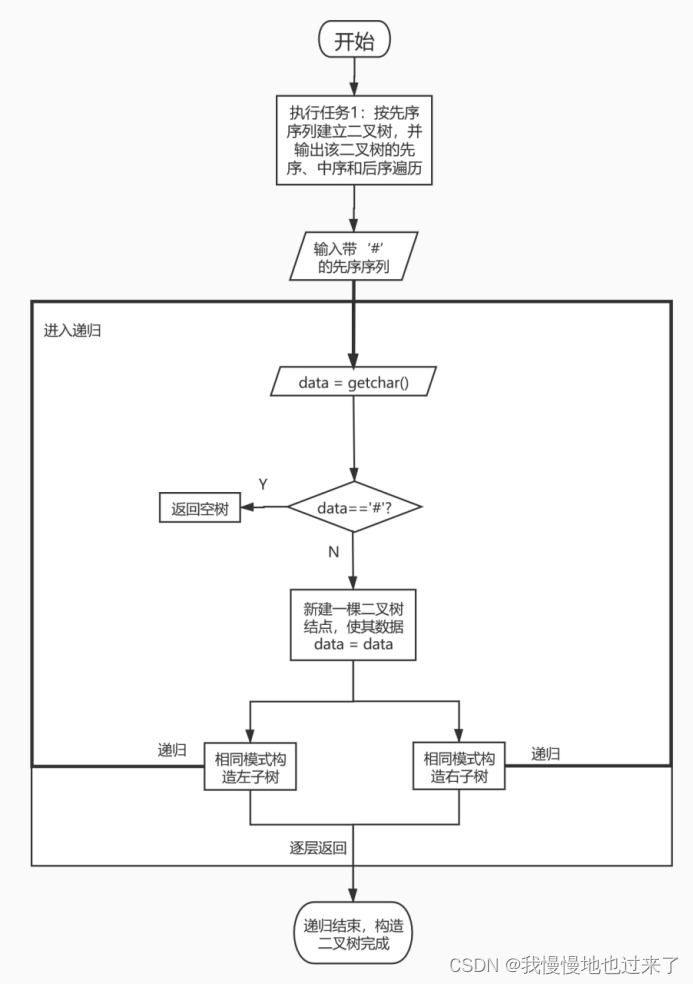
图 2
任务1中先序、中序和后序遍历算法流程图如图3所示。

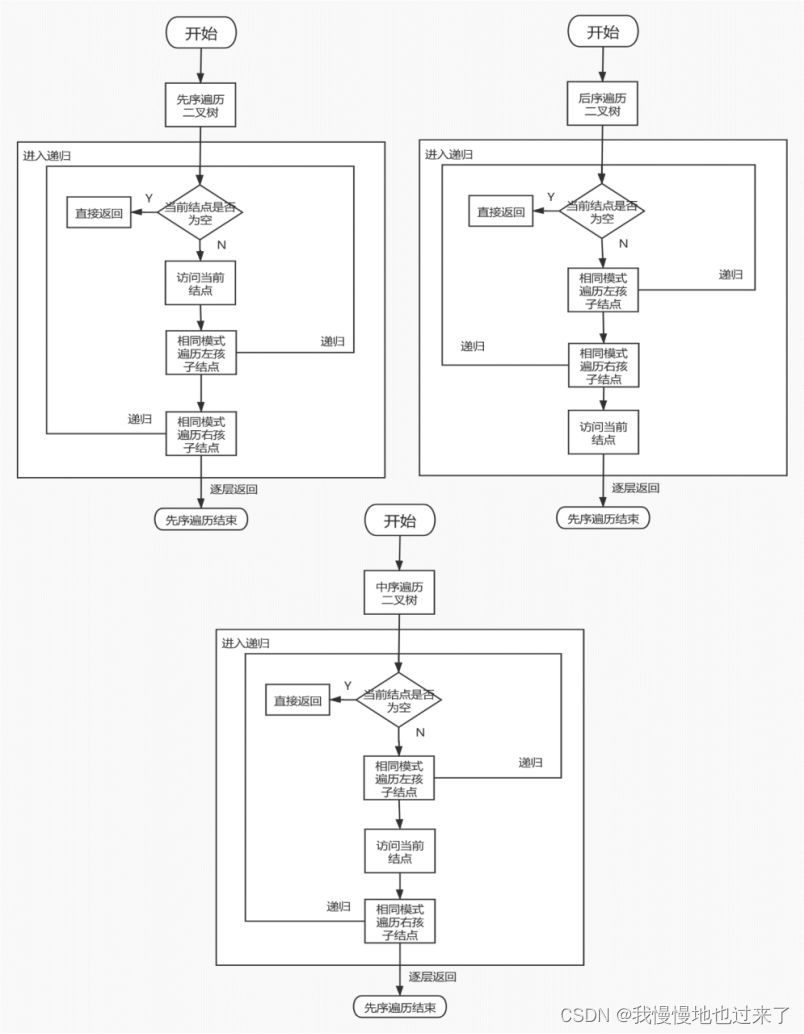
图 3
（2）任务2中核心算法流程图如图4所示

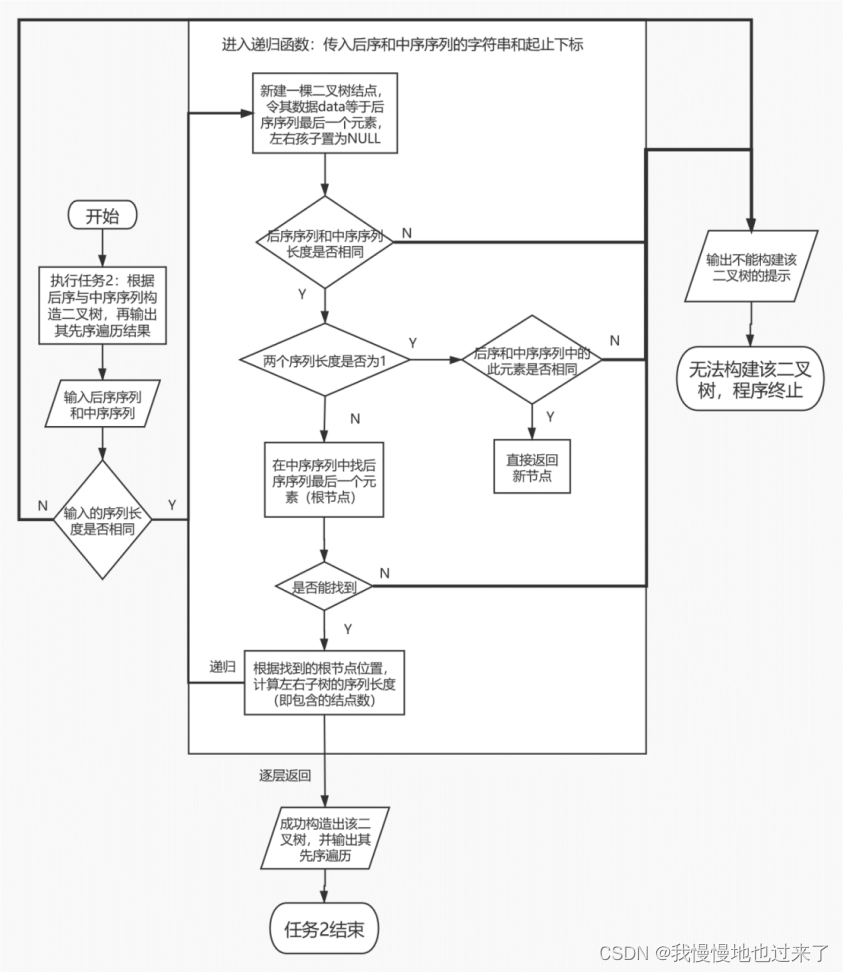
图 4

（3）任务3统计二叉树叶子数和宽度的流程图，如图5所示。

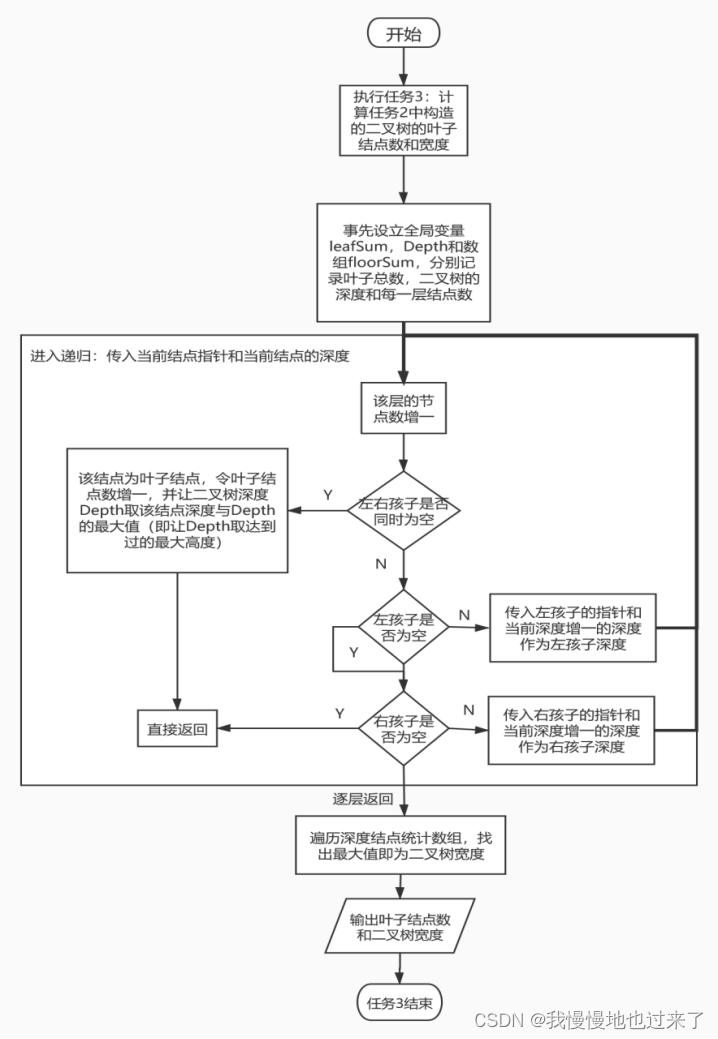
图 5
（4）任务4判断两颗二叉树是否等价的流程图，如图6所示

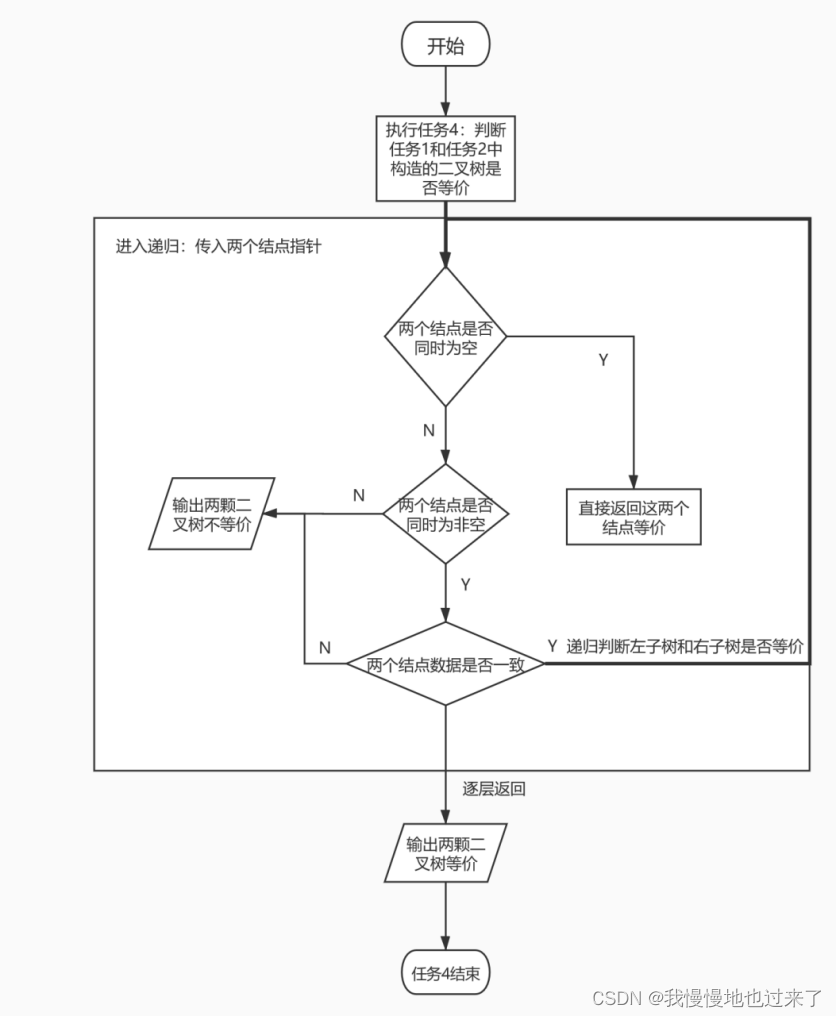
三、用户手册

首先，程序会提示： Create Tree1 in PreOrder 这是任务1：输入先序序列来构造一棵二叉树。此时您要输入一段带‘#’的字符串，表示一棵二叉树的先序序列，‘#’代表空结点。这里假设您输入“DCB##A##E##”。接着程序会执行任务1，以您输入的先序序列构造一棵二叉树，并输出该二叉树的先序遍历、中序遍历和后序遍历结果。如下所示： start task (1) Create Tree in PreOrder preOrderTraverse： DCBAE inOrderTraverse： BCADE postOrderTraverse：

BACED ------------------------------------------------
然后是执行任务2的内容，输入后序序列和中序序列来构造二叉树，程序提示如下： start task (2) Input the postOrder and inOrder Sequence ,Then build the tree please input the postOrder sequence 您需要先输入一段不带‘#’的字符串，表示后序序列。这里如果您输入了“BACED”，程序会继续提示： please input the inOrder sequence 这时要输入一段不带‘#’的字符串，表示中序序列，这时如果您输入了“EBADC”，程序会提示： Unable to build a binary tree. 这表明您输入的后序序列和中序序列是无法构造一棵二叉树的，程序会就此终止，不会再继续执行剩下的任务。而如果我们输入了一棵二叉树正确的后序序列和中序序列，如后序序列为“DECBHIGJFA”，中序序列为“DCEBAHGIFJ”，程序会输出该二叉树的先序遍历结果：
preOrderTraverse:
ABCDEFGHIJ ------------------------------------------------
如果您输入的后序序列过长（程序设定最长不超过30个字符），程序同样会提示无法构建一棵二叉树。 如果在任务2中成功构建了一棵二叉树并输出了它的先序序列后，就会接着执行任务3，统计任务2中构造的二叉树的叶子结点数和宽度。这里无需输入，程序自动执行，以上面正确执行任务2的情况为例，会显示： start task (3) The number of leaf nodes of the tree is: 5 The width of the tree is:4

表明该二叉树叶子结点数为5个，宽度为4。
最后程序会执行任务4，判断任务1和任务2中构造的二叉树是否等价。这里同样无需输入，程序会在任务3结束后自动执行任务4。如果等价，会输出：
start task (4) Are two Bitrees equivalent?
1
否则输出
start task (4) Are two Bitrees equivalent?
0
由于任务3和任务4无需任何输入，所以在任务2输入完中序序列后，不管是否可以构造一棵二叉树，程序都会直接执行到末尾结束。

四、结果

（1）任务2中无法构建一棵二叉树的情况，如图 7和图 8所示。

图 7

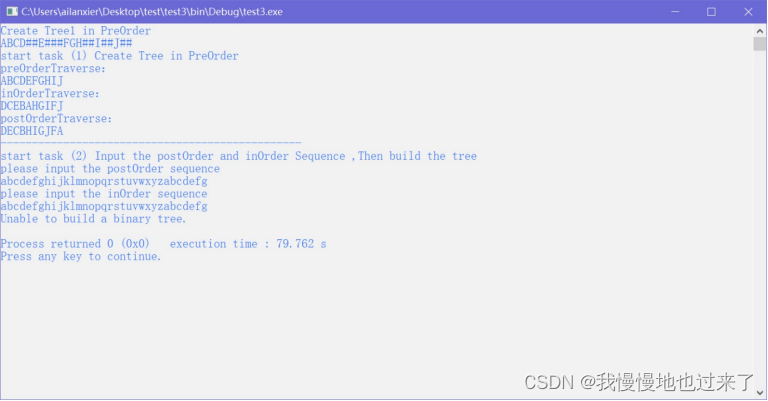
图 8

（2）任务2与任务1中构造的二叉树等价的情况，如图9所示。

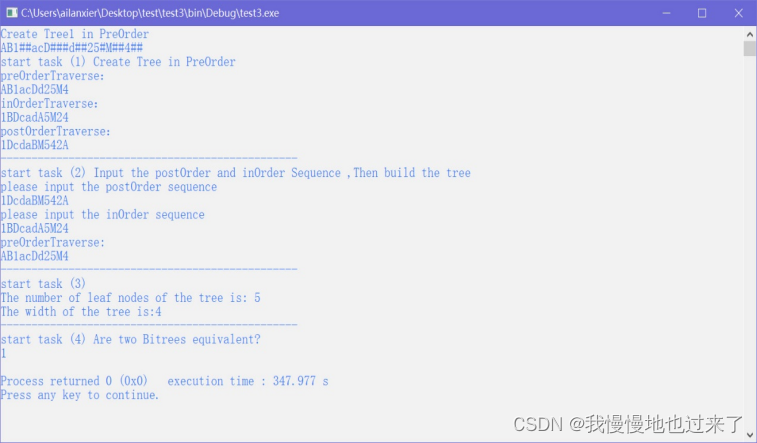
图 9
（3）任务2与任务1中构造的二叉树不等价的情况，如图10所示

图 10

五、总结

本次实验主要学习了以二叉链表为存储结构的二叉树数据结构。在构建二叉树的过程中，不同的任务分别采取了两种“不同”的方式。第一种是通过输入带‘#’的先序序列来构建二叉树，因为带‘#’的序列唯一确定一棵二叉树，所以可以只利用先序序列的性质，按先序递归构建了二叉树；第二种是通过输入不带‘#’的后序序列和中序序列来构建二叉树，这个难度较大，需要经过一定的模拟和递归才能实现。第二种方式实质还是通过先序递归来构建二叉树，但是要通过对后序和中序序列的同时解析后才可以完成。在构建二叉树后，还进行了二叉树经典的三个遍历：先序、中序和后序遍历。通过递归，遍历二叉树的操作是简单的，只需要稍微调整访问结点的顺序即可。任务3和任务4不能仅仅进行简单的遍历，要在遍历时获取信息。这时的遍历属于深度优先搜索，需要访问所有结点才能获得正确的结果。在搜索的同时进行信息的检索，比较和判断，对递归能力提出了更高的要求。
不同于之前的实验，本次任务中几乎每一个关键算法都是通过递归实现的，这主要依赖于二叉树优秀的复用性和对称性。同时，灵活简洁的递归语句也会增大程序出现bug的几率，因为递归不容易看穿所有的特殊情况和进行debug，常常会出现意料之外的崩溃情况。所以在编写递归函数的时候，一定要清醒地理清到各种终止条件和特殊情况，并通过输入多组测试数据，尽可能发现还躲在暗处的bug。同时因为本次实验过程时间长，任务量大，在有限的时间内容易紧张而忽视一些隐蔽的细节，这也是我还需要提升的能力。
经过这次实验，我锻炼了分析问题和编写递归程序的能力，大大提高了debug的能力，可以更加迅速地定位存在的隐蔽问题，对于程序的细节有了更深的认识。最重要的，是掌握了二叉树的多种构造方法和遍历手段，对二叉树的认识在实践中进一步加深，也为以后图的学习奠定了一定的基础。不足的是一些细节在课上提交时未能及时纠正，在课后写报告时才逐渐完善。所以短时间的编程能力还需继续增强。