Python实现分位数回归模型(quantreg算法)项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

分位数回归是简单的回归，就像普通的最小二乘法一样，但不是最小化平方误差的总和，而是最小化从所选分位数切点产生的绝对误差之和。

本项目通过quantreg回归算法来构建分位数回归模型。

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

编号	变量名称	描述
1	x1
2	x2
3	x3
4	x4
5	x5
6	x6
7	x7
8	x8
9	x9
10	x10
11	y	因变量

数据详情如下(部分展示)：

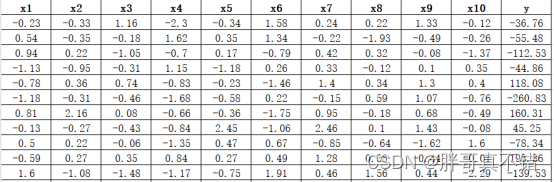
3.数据预处理

3.1?用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

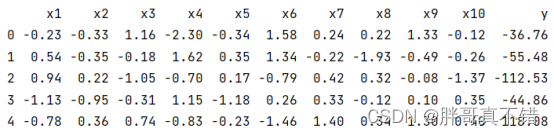
关键代码：

3.2 数据缺失查看

使用Pandas工具的info()方法查看数据信息：

????

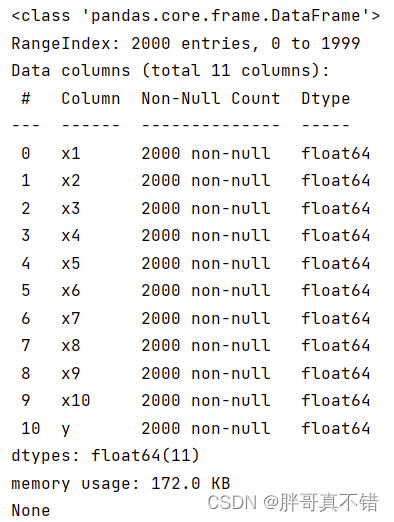从上图可以看到，总共有11个变量，数据中无缺失值，共2000条数据。

关键代码：

3.3?数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

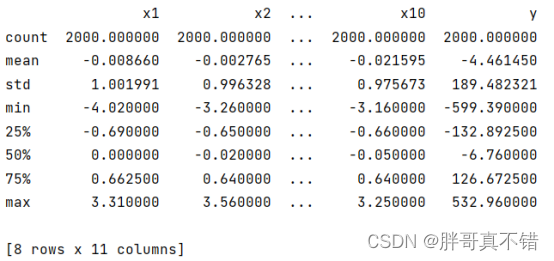
关键代码如下： ?

4.探索性数据分析

4.1?y变量直方图

用Matplotlib工具的hist()方法绘制直方图：

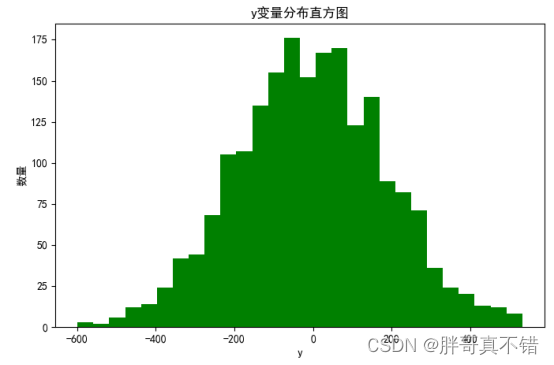
从上图可以看到，y变量主要集中在-400~400之间。

4.2 相关性分析

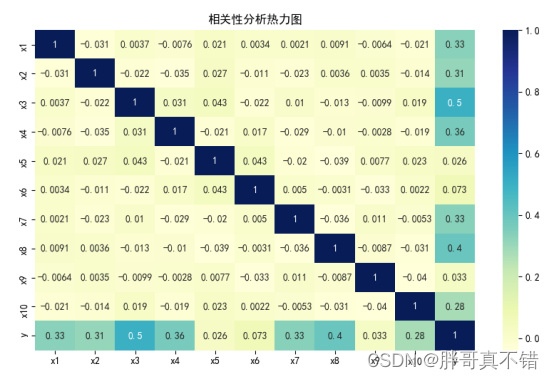
从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。

5.特征工程

5.1 建立特征数据和标签数据

关键代码如下：

5.2 数据集拆分

通过train_test_split()方法按照80%训练集、20%测试集进行划分，关键代码如下：

6.构建分位数回归模型

主要使用分位数回归算法，用于目标回归。

6.1 构建模型

编号	模型名称	参数
1	分位数回归模型	q=0.5

6.2 模型摘要信息

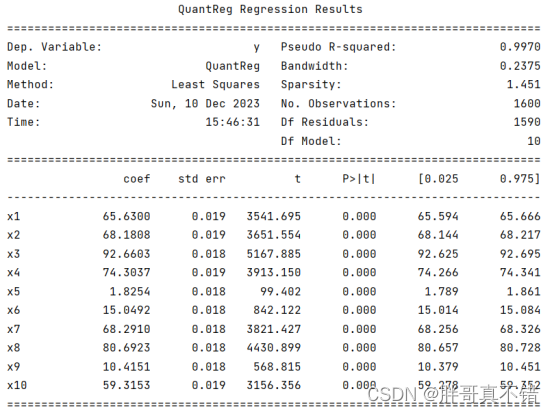
7.模型评估

7.1?评估指标及结果

评估指标主要包括可解释方差值、平均绝对误差、均方误差、R方值等等。

模型名称	指标名称	指标值
测试集
分位数回归模型	??R方	1.0
	均方误差	0.3202
	可解释方差值	1.0
	平均绝对误差	0.4571

从上表可以看出，R方为1.0，说明模型效果较好。

关键代码如下：

7.2?真实值与预测值对比图

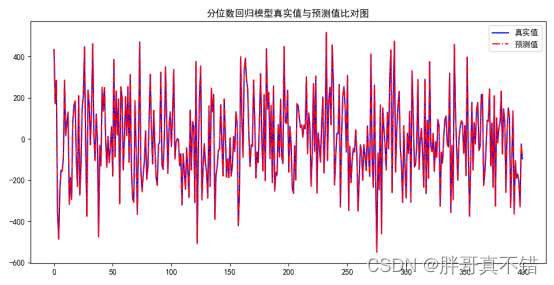
从上图可以看出真实值和预测值波动基本一致。 ???

8.结论与展望

综上所述，本文采用了分位数回归算法来构建回归模型，最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。

# 本次机器学习项目实战所需的资料，项目资源如下：
 
# 项目说明：

# 获取方式一：
 
# 项目实战合集导航：
 
https://docs.qq.com/sheet/DTVd0Y2NNQUlWcmd6?tab=BB08J2
 
# 获取方式二：

链接：https://pan.baidu.com/s/1d2YniPcRMJ2O9grRv4Ydfw 
提取码：7brs