Python - 深夜数据结构与算法之 Greedy

目录

一.引言

二.贪心的简介

1.贪心算法

2.适用场景

三.经典算法实战

1.Jump-Game-2 [45]

2.Jump-Game [55]

3.Max-Profit [122]

4.Assign-Cookies [455]

5.Lemonade-Change [860]

四.总结

---

一.引言

本节带来算法中比较经典的贪心算法，它和动态规划有一定相似性但又有不同，下面我们看一下贪心算法的流程以及一些相关的算法题目。

二.贪心的简介

1.贪心算法

贪心算法要求每一步选择都在当前状态下取最好，但最后结局并不一定是全局最好的，用老话讲就是只顾眼前，难听的话讲就是鼠目寸光， 但是在特定情况下贪心算法也有其用武之地，比如我们在某一步用贪心算法，而其他整体用递归、遍历等等，相当于做一个辅助的步骤。

这里大家可以先对贪心、回溯以及动态规划的特点进行了解，后续也会进行分解。

2.适用场景

这里贪心没有太明确的代码模版，我们只需要每一步都找最优即可，但是需要找到其适应场景。

◆ 贪心算法正例

给定一个总数和多种面额的硬币，求凑出总金额的最小硬币数。这里 total=36，给出的硬币是 20、10、5、1，我们每次贪心找最大，正好可以四次解决。

◆ 贪心算法反例

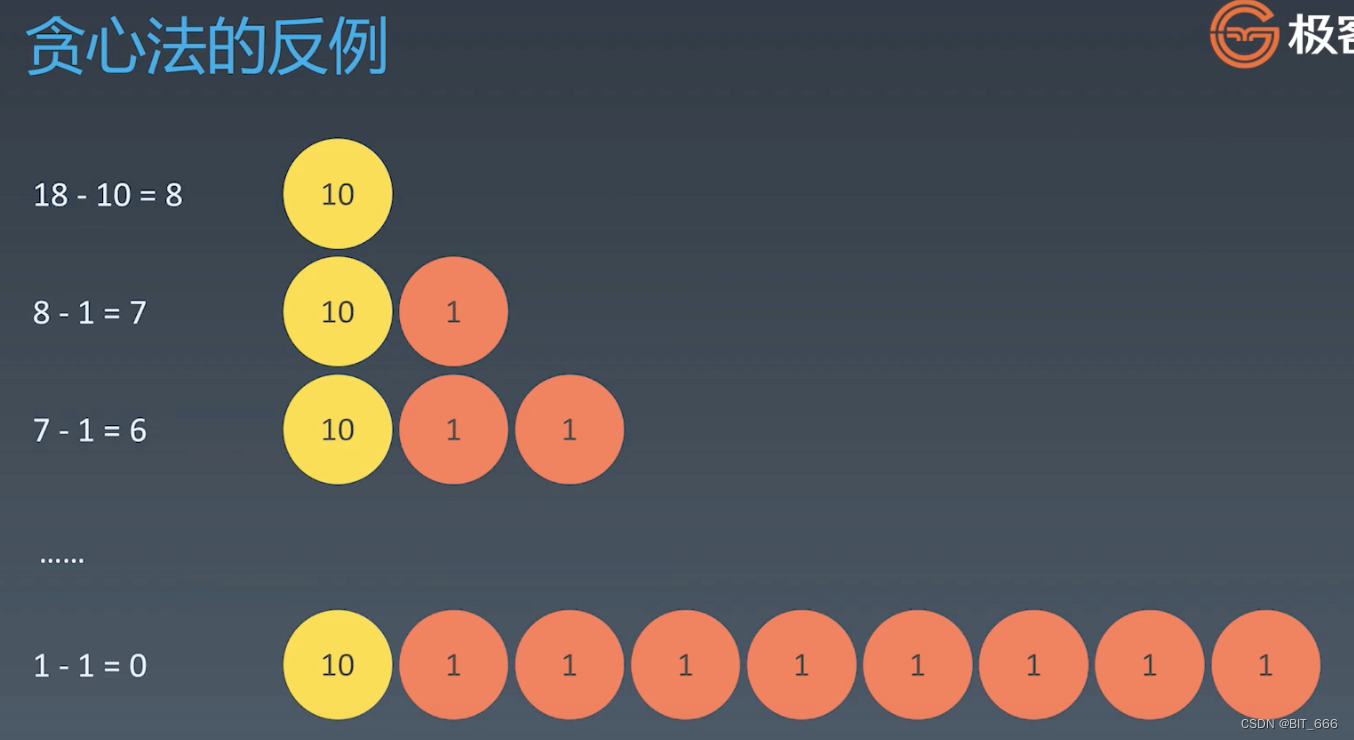
还是上面的例子，这次硬币换为 10、9、1，total = 18，如果我们还是使用贪心的话，第一个硬币最大取10，则剩下的 8 需要 8x1 个1元硬币，这当然不是最优的，因为 2x9 即可完成。

◆ 贪心算法场景

我们想要使用贪心算法需要一定的先决条件，或者证明当前算法适合使用贪心，例如上面的案例，如果我们的硬币是成倍数关系，那我们用贪心是合适的，因为用 1x10 肯定比 2x5 的硬币数量少。所以最关键的就是需要证明这个题贪心是合适的，我们再使用贪心。

三.经典算法实战

1.Jump-Game-2 [45]

跳跃游戏2:?https://leetcode.cn/problems/jump-game-ii/description/

◆ 题目分析

贪心的思路，每一个 index 都向前走最大步数并记录能走到的最大的覆盖范围，即 next_position。在 index -> next_position 的过程中，记录新的最大范围，当遍历到 index 时，如果新的最大范围即 next_position 变大了，则更新并再走一步，否则不用走，因为多走一步也没有之前一步远。

◆ 贪心实现

class Solution(object):
    def jump(self, nums):

        if len(nums) == 1:
            return 0

        step = 0
        max_cover = 0
        next_position = 0

        for index in range(len(nums)):
            # 每一步看当前能到的最大范围
            max_cover = max(index + nums[index], max_cover)

            # 由于上一步已经覆盖前面的 index
            # 所以前面几个 index 都是 1xStep 能够走到的
            if index == next_position:
                step += 1
                # 走到 next_position 时，更新 cover 面积
                next_position = max_cover
                
                if max_cover >= len(nums) - 1:
                    break

        return step

代码其实就是在找这个红条，确定了第一次的 next_position 后，就只更新，直到 next_position 才判断第二个条子的范围，因为我们可以 1xstep 到达 next_position，就没必要多走。?

2.Jump-Game [55]

跳跃游戏:?https://leetcode.cn/problems/jump-game/description/

◆ 题目分析

遍历一遍数组，每次维护当前可走的最远路径，如果最远路径超过最后的索引，则可以走到终点。

◆ 贪心实现

class Solution(object):
    def canJump(self, nums):
        """
        :type nums: List[int]
        :rtype: bool
        """

        cur_max, n = 0, len(nums)
        for i in range(n - 1):

            # 当前索引为0，如果 cur_max 不超过 i 则无法继续走
            if nums[i] == 0 and cur_max < i + 1:
                break

            # 步长 + 当前索引 = 当前能去的最远索引
            cur_step = nums[i] + i
            cur_max = max(cur_max, cur_step)

            # 满足条件直接退出
            if cur_max >= n - 1:
                return True

        return cur_max >= n - 1

第一版实现时博主没有加 break 的索引，导致 [0, 2,?3] 这样的示例无法通过，所以我们需要判断 cur_max 是否能走到 0 [位置i] 后面的位置即 i+1，如果不能则走到 0 或者连 0 都走不到，那后面就走不动了。

3.Max-Profit [122]

股票最佳卖出时机:?https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii

◆ 题目分析

这里我们相当于是拥有观星技能的诸葛亮，所以只要我们今天比昨天高，我们就能实现一次正收益的买入卖出操作，所以用两个指针分别查看昨天、今天即可，注意这里不是昨天、今天、明天，因为这个是小品。

◆ 贪心实现

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """

        reward = 0

        for i in range(0, len(prices) - 1):
            yesterday = prices[i]
            today = prices[i+1]
            # 今天比昨天高就买，赚一天是一天
            if today > yesterday:
                reward += today - yesterday
        
        return reward

主打一个赚一天是一天，观星就完事了。

4.Assign-Cookies [455]

饼干分发:?https://leetcode-cn.com/problems/assign-cookies/

◆ 题目分析

用有限的饼干尽可能满足更多孩子的胃口，大的饼干给胃口大的，小的饼干给胃口小的，浪费最小。

◆ 贪心实现

class Solution(object):
    def findContentChildren(self, g, s):
        """
        :type g: List[int]
        :type s: List[int]
        :rtype: int
        """

        # 最大的饼干优先给胃口最大的孩子
        g.sort()
        s.sort()

        # 记录满足个数
        satisfied = 0

        while g and s:
            # 能满足，吃掉一块
            if s[-1] >= g[-1]:
                s.pop()
                g.pop()
                satisfied += 1
            # 不能满足，胃口太大，换下一个小孩
            else:
                g.pop()

        return satisfied

因为贪心，所以我们进行排序从大的开始供给。

5.Lemonade-Change [860]

柠檬水找零:?https://leetcode.cn/problems/lemonade-change/description/?

◆ 题目分析

题目给了三种硬币类型，首先判断 3 种情况，即收到 5 元留下，收到 10 元找 5，收到 20 找 10 + 5 或者 5 +5 + 5，前面两个状态是固定的，有就是有，没有就 False 了，需要贪心的是第三步。这里我们为顾客找钱，先找 10 块不会出错，因为如果同时满足?10 + 5 和 5 + 5 + 5 两种情况，先找 10 + 5 是最好的，因为剩下的两个 5 还能找 2 个 10 块，如果一次性给 3 个 5，那么后面再来 10 块就不好找了。所以这里贪心就是给 20 的时候优先找最大的。

◆ 贪心实现

class Solution(object):
    def lemonadeChange(self, bills):
        """
        :type bills: List[int]
        :rtype: bool
        """

        five, ten = 0, 0

        for bill in bills:
            if bill == 5:
                five += 1
            elif bill == 10:
                # 10 块的时候需要至少有一个 5 块
                if five < 1: return False
                five -= 1
                ten += 1
            else:
                # 20 的时候必须有 10+5 or 5+5+5，否则无法找零
                if ten > 0 and five > 0:
                    ten -= 1
                    five -= 1
                elif five > 2:
                    five -= 3
                else:
                    return False
        
        return True

用 five 和 ten 记录商家手里硬币的情况，10 块或 20 块找不开的时候 return False。

四.总结

贪心算法在代码上相对简洁，但是想到能用贪心算法解决比较难。上面的题目很多都可以用动态规划去做，但是相对贪心会有一定复杂度的提升，因为动规相当于不断试错的过程，而贪心则是一步到位，后面我们讲解动态规划时，大家也可以回头再看下这些题目。