数据结构与算法教程，数据结构C语言版教程！（第五部分、数组和广义表详解）四

?第五部分、数组和广义表详解

数组和广义表，都用于存储逻辑关系为“一对一”的数据。

数组存储结构，99% 的编程语言都包含的存储结构，用于存储不可再分的单一数据；而广义表不同，它还可以存储子广义表。

本章重点从矩阵的角度讨论二维数组的存储，同时讲解广义表的存储结构以及有关其广度和深度的算法实现。

七、矩阵（稀疏矩阵）的转置算法（C语言）详解

矩阵（包括稀疏矩阵）的转置，即互换矩阵中所有元素的行标和列标，如图 1 所示：

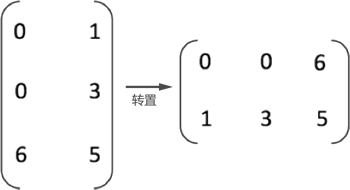
图 1 矩阵转置示意图

但如果想通过程序实现矩阵的转置，互换行标和列标只是第一步。因为实现矩阵转置的前提是将矩阵存储起来，数据结构中提供了 3 种存储矩阵的结构，分别是三元组顺序表、行逻辑链接的顺序表和十字链表。如果采用前两种结构，矩阵的转置过程会涉及三元组表也跟着改变的问题，如图 2 所示：

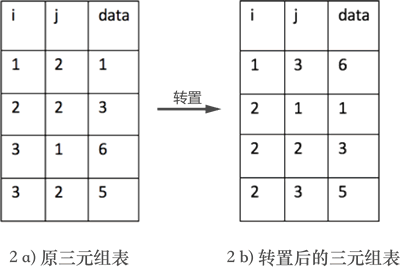
图 2 三元组表的变化

图 2a) 表示的是图 1 中转置之前矩阵的三元组表，2b) 表示的是图 1 中矩阵转置后对应的三元组表。

不仅如此，如果矩阵的行数和列数不等，也需要将它们互换。

因此通过以上分析，矩阵转置的实现过程需完成以下 3 步：

1. 将矩阵的行数和列数互换；
2. 将三元组表（存储矩阵）中的 i 列和 j 列互换，实现矩阵的转置；
3. 以 j 列为序，重新排列三元组表中存储各三元组的先后顺序；

此 3 步中，前两步比较简单，关键在于最后一步的实现。本节先介绍较容易的一种。

矩阵转置的实现思路是：不断遍历存储矩阵的三元组表，每次都取出表中 j 列最小的那一个三元组，互换行标和列标的值，并按次序存储到一个新三元组表中。

例如，将图 2a) 三元组表存储的矩阵进行转置的过程为：

1. 新建一个三元组表（用于存储转置矩阵），并将原矩阵的行数和列数互换赋值给新三元组；
2. 遍历三元组表，找到表中 j 列最小值 1 所在的三元组 (3,1,6)，然后将其行标和列标互换后添加到一个新的三元组表中，如图 3 所示：

   

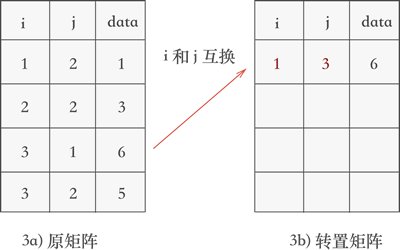
   图 3 矩阵转置的第一个过程

3. 继续遍历三元组表，找到表中 j 列次小值为 2 的三元组，分别为 (1,2,1)、(2,2,3) 和 (3,2,5)，根据找到它们的先后次序将各自的行标和列标互换后添加到新三元组表中，如图 4 所示：

   

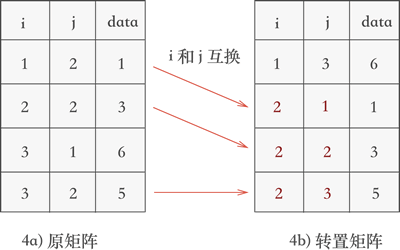
   图 4 矩阵转置的第二个过程

对比图 4 和图 2b) 可以看到，矩阵被成功地转置。

因此，矩阵转置的 C 语言实现代码为：

#include<stdio.h>

#define number 10

typedef struct { ???

????????int i, j; ???

????????int data;

}triple;

typedef struct { ???

????????triple data[10]; ???

????????int n, m, num;

}TSMatrix;

TSMatrix transposeMatrix(TSMatrix M, TSMatrix T) { ???

????????T.m = M.n; ???

????????T.n = M.m; ???

????????T.num = M.num; ???

????????if (T.num) { ???????

????????????????int q = 0; ???????

????????????????for (int col = 1; col <= M.m; col++) { ???????????

????????????????????????for (int p = 0; p < M.num; p++) { ???????????????

????????????????????????????????if (M.data[p].j == col) { ???????????????????

????????????????????????????????????????T.data[q].i = M.data[p].j; ???????????????????

????????????????????????????????????????T.data[q].j = M.data[p].i; ???????????????????

????????????????????????????????????????T.data[q].data = M.data[p].data; ???????????????????

????????????????????????????????????????q++; ???????????????

????????????????????????????????} ???????????

????????????????????????} ???????

????????????????} ???

????????} ???

????????return T;

}

int main() { ???

????????TSMatrix M; ???

????????M.m = 2; ???

????????M.n = 3; ???

????????M.num = 4; ???

????????M.data[0].i = 1; ???

????????M.data[0].j = 2; ???

????????M.data[0].data = 1; ???

????????M.data[1].i = 2; ???

????????M.data[1].j = 2; ???

????????M.data[1].data = 3; ?

??

????????M.data[2].i = 3; ???

????????M.data[2].j = 1; ???

????????M.data[2].data = 6; ???

????????M.data[3].i = 3; ???

????????M.data[3].j = 2; ???

????????M.data[3].data = 5; ???

????????TSMatrix T; ???

????????for (int k = 0; k < number; k++) { ???????

????????????????T.data[k].i = 0; ???????

????????????????T.data[k].j = 0; ???????

????????????????T.data[k].data = 0; ???

????????} ???

????????T = transposeMatrix(M, T); ???

????????for (int i = 0; i < T.num; i++) { ???????

????????????????printf("(%d,%d,%d)\n", T.data[i].i, T.data[i].j, T.data[i].data); ???

????????} ???

????????return 0;

}

程序运行结果为：

(1,3,6)
(2,1,1)
(2,2,3)
(2,3,5)

由于此算法中嵌套使用了两个 for 循环，时间复杂度为O（）。

---

?八、稀疏矩阵的快速转置算法（C语言）详解

《矩阵的转置算法》一节介绍了实现矩阵转置的普通算法，该算法的时间复杂度为O（）。本节给大家介绍一种实现矩阵转置更高效的算法，通常称为稀疏矩阵的快速转置算法。

我们知道，稀疏矩阵的转置需要经历以下 3 步：

1. 将矩阵的行数和列数互换；
2. 将三元组表（存储矩阵）中的 i 列和 j 列互换，实现矩阵的转置；
3. 以 j 列为序，重新排列三元组表中存储各三元组的先后顺序；

稀疏矩阵快速转置算法和普通算法的区别仅在于第 3 步，快速转置能够做到遍历一次三元组表即可完成第 3 步的工作。

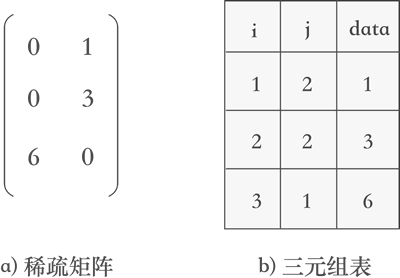
图 1 稀疏矩阵和对应的三元组表

如图 1 所示，此为转置之前的矩阵和对应的三元组表。稀疏矩阵的快速转置是这样的，在普通算法的基础上增设两个数组（假设分别为 array 和 copt）：

• array 数组负责记录原矩阵每一列非 0 元素的个数。以图 1 为例，则对应的array数组如图 2 所示：

  

  图 2 每一列非 0 元素的个数

  图 2 中 array 数组表示，原稀疏矩阵中第一列有 1 个非 0 元素，第二列有 2 个非 0 元素。
• copt 数组用于计算稀疏矩阵中每列第一个非 0 元素在新三元组表中存放的位置。我们通常默认第一列首个非 0 元素存放到新三元组表中的位置为 1，然后通过 cpot[col] = cpot[col-1] + array[col-1] 公式可计算出后续各列首个非 0 元素存放到新三元组表的位置。拿图 1 中的稀疏矩阵来说，它对应的 copt 数组如图 3 所示：

  

  图 3 copt 数组示意图

  图 3 中的 copt 数组表示，原稀疏矩阵中第 2 列首个非 0 元素存放到新三元组表的位置为 2。

注意，cpot[col] = cpot[col-1] + array[col-1] 的意思是，后一列首个非 0 元素存放的位置等于前一列首个非 0 元素的存放位置加上该列非 0 元素的个数。由此可以看出，copt 数组才是最终想要的，而 array 数组的设立只是为了帮助我们得到 copt 数组。

这样在实现第 3 步时，根据每个三元组中 j 的数值，可以借助 cpot 数组直接得到此三元组新的存放位置，C 语言实现代码如下：

//实现快速转置算法的函数

TSMatrix fastTransposeMatrix(TSMatrix M,TSMatrix T){

//第1步：行和列置换

????????T.m=M.n;

????????T.n=M.m;

????????T.num=M.num;

????????if (T.num) {

????????????????//计算array数组

????????????????int array[number];

????????????????for (int col=1; col<=M.m; col++) {

????????????????????????array[col]=0;

????????????????}

????????????????for (int t=0; t<M.num; t++) {

????????????????????????int j=M.data[t].j;

????????????????????????array[j]++;

????????????????}

????????????????//创建并初始化cpot数组

????????????????int cpot[T.m+1];

????????????????cpot[1]=1;//第一列中第一个非0元素的位置默认为1

????????????????for (int col=2; col<=M.m; col++) {

????????????????????????cpot[col]=cpot[col-1]+array[col-1];

????????????????}

????????????????//遍历一次即可实现三元组表的转置

????????????????for (int p=0; p<M.num; p++) {

????????????????????????//提取当前三元组的列数

????????????????????????int col=M.data[p].j; /

????????????????????????/根据列数和cpot数组，找到当前元素需要存放的位置

????????????????????????int q=cpot[col];

????????????????????????//转置矩阵的三元组默认从数组下标0开始，而得到的q值是单纯的位置，所以要减1

????????????????????????T.data[q-1].i=M.data[p].j;

????????????????????????T.data[q-1].j=M.data[p].i;

????????????????????????T.data[q-1].data=M.data[p].data?;

??????????????????????? //存放完成后，cpot数组对应的位置要+1，以便下次该列存储下一个三元组

????????????????????????cpot[col]++;

????????????????}

????????}

????????return T;

}

使用 fastTransposeMatrix 函数实现图 1 中稀疏矩阵转置的 C 语言完整程序为：

#include<stdio.h>

#define number 10

typedef struct {

????????int i,j;

????????int data;

}triple;

typedef struct {

????????triple data[number];

????????int rpos[number];

????????int n,m,num;

}TSMatrix;

//fastTransposeMatrix放置位置

int main() {

????????TSMatrix M;

????????M.m=2;

????????M.n=3;

????????M.num=3;

????????M.data[0].i=1;

????????M.data[0].j=2;

????????M.data[0].data=1;

????????M.data[1].i=2;

????????M.data[1].j=2;

????????M.data[1].data=3;

????????M.data[2].i=3;

????????M.data[2].j=1;

????????M.data[2].data=6;

????????TSMatrix T;

????????T=fastTransposeMatrix(M, T);

????????printf("转置矩阵三元组表为：\n");

????????for (int i=0; i<T.num; i++) {

????????????????printf("(%d,%d,%d)\n",T.data[i].i,T.data[i].j,T.data[i].data);

????????}

????????return 0;

}

程序运行结果为：

转置矩阵三元组表为：
(1,3,6)
(2,1,1)
(2,2,3)

可以看出，稀疏矩阵快速转置算法的时间复杂度为?O(n)。即使在最坏的情况下（矩阵中全部都是非 0 元素），该算法的时间复杂度也才为O（）。