代码随想录27期|Python|Day27|回溯算法|39.组合总和|40.组合总和II|131.分割回文串
发布时间:2023年12月27日
39.?组合总和
在Day24组合问题的模版上加上了一个“可以重复选用当前值”的选项,递归中调用backtracking的idx由i + 1改为i:
self.backtracking(i, path, res, candidates, target) # 起始位置变成i,可以重复使用当前的值class Solution(object):
def combinationSum(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
res = []
self.backtracking(0, [], res, candidates, target)
return res
def backtracking(self, idx, path, res, candidates, target):
# 终止条件
if target < 0:
return
if target == 0:
res.append(path[:]) # 加入res
return # 回溯
for i in range(idx, len(candidates)):
path.append(candidates[i])
target -= candidates[i]
self.backtracking(i, path, res, candidates, target) # 起始位置变成i,可以重复使用当前的值
target += candidates[i]
path.pop() # 回溯?40.?组合总和 II
本题需要注意去重:首先对于树进行排序。其次需要明确的是,在一个树枝上是不需要去重的,但是对于同一层,是需要去重的。也就是一个组合内,可以出现重复数字,但是不能两个组合相同。
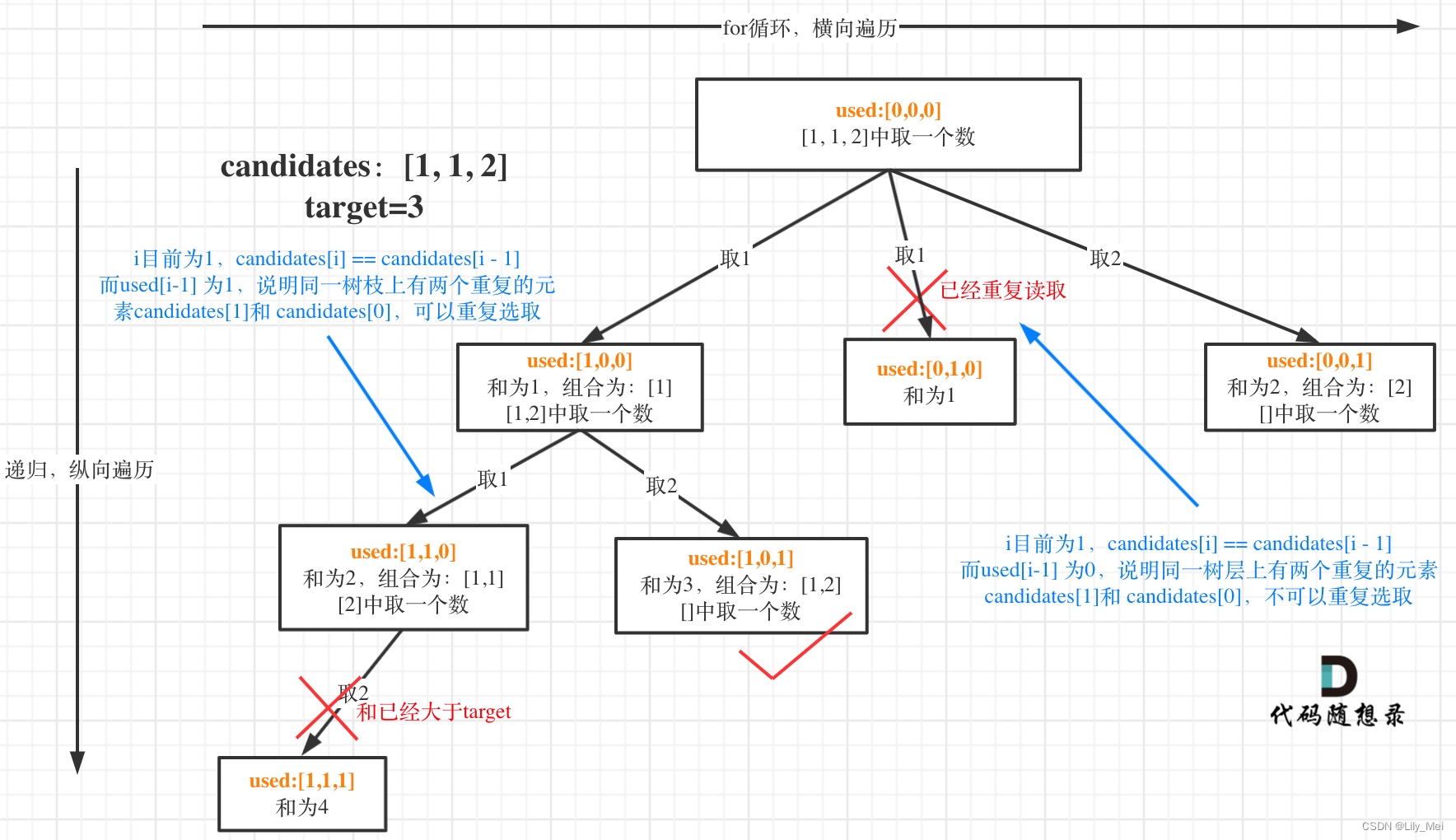
所以需要在i遍历的时候先判读是不是重复的,然后再递归。也就是平行移动的时候需要考虑,但是在纵向移动的时候不用。
class Solution(object):
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
res = []
candidates = sorted(candidates)
used = [] * len(candidates)
self.backtracking(0, [], res, candidates, target)
return res
def backtracking(self, idx, path, res, candidates, target):
# 终止条件
if target < 0:
return
if target == 0:
res.append(path[:]) # 加入res
return # 回溯
for i in range(idx, len(candidates)):
# 如果后面一个和前面一个是相等的,那么他们所组成的组合一定有相同的
if i > idx and candidates[i] == candidates[i-1]:
continue
path.append(candidates[i])
target -= candidates[i]
self.backtracking(i + 1, path, res, candidates, target) # 起始位置变成i,可以重复使用当前的值
target += candidates[i]
path.pop() # 回溯?131.?分割回文串
本题的特殊点在于对于数字的分割,需要传入下一层级的其实是分割之后的子序列,其次还有对于回文字判断,相当于在回溯前加了一个if条件。
class Solution(object):
def partition(self, s):
"""
:type s: str
:rtype: List[List[str]]
"""
res = []
self.backtracking([], 0, s, res)
return res
def backtracking(self, path, start_idx, s, res):
if start_idx == len(s):
res.append(path[:])
return
for i in range(start_idx, len(s)):
# 多了一步:判断是否是回文数
if self.ispalindrome(start_idx, i, s):
path.append(s[start_idx:i+1]) # 在i处切段
self.backtracking(path, i + 1, s, res) # 传入断点索引作为新的start_idx
path.pop()
def ispalindrome(self, start_idx, cur, string):
i = start_idx
j = cur
while i <= j:
if string[i] != string[j]:
return False
i += 1
j -= 1
return True判断回文字也不需要使用函数,可以使用[::-1]来判断两个序列是否相等:
if s[start_index: i + 1] == s[start_index: i + 1][::-1]:也可以使用all来简洁书写:
def isPalindrome(self, s):
return all(s[i] == s[len(s) - 1 - i] for i in range(len(s) // 2))
文章来源:https://blog.csdn.net/m0_57527624/article/details/135204181
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!