文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《含规模氢能综合利用的高比例风光多能源系统低碳灵活调度》

这个标题涵盖了几个关键概念，让我们逐一解读：

1. 规模氢能综合利用：

   • 规模氢能：?指的是在大规模范围内应用氢能技术，可能包括制备、存储和利用氢能的系统。
   • 综合利用：?意味着不仅仅是单一方面的利用，而是将氢能与其他能源或系统相结合，实现多方面的应用。

2. 高比例风光多能源系统：

   • 高比例风光：?指的是系统中占主导地位的能源是风能和光能，这两者通常是可再生的、环保的能源。
   • 多能源系统：?指的是整个系统不依赖于单一能源，而是整合了多种不同类型的能源。

3. 低碳灵活调度：

   • 低碳：?意味着系统的运行和能源利用过程中产生的碳排放较少，符合低碳经济的要求。
   • 灵活调度：?指的是系统具备在不同条件下灵活调整能源利用和分配的能力，以适应变化的需求和环境条件。

因此，整个标题可以理解为描述一种能源系统，该系统具有大规模应用氢能技术，以及在系统中风光能占据主导地位，同时系统具备低碳特性和灵活的调度能力。这种综合利用多种能源的系统可能具有更好的环境友好性和适应性，同时在能源转型和可持续发展方面发挥积极作用。

摘要：随着风光等间歇性可再生能源大规模增长和并网，可再生能源弃能率升高与系统备用灵活性问题日益突出，为解决高比例可再生能源科学消纳与能源系统灵活稳定运行问题，提出一种含规模氢能综合利用的高比例风光多能源系统低碳灵活调度方法。针对电制氢、氢燃料电池、甲烷反应器等组成的氢能综合利用单元进行机理分析并建模，研究该单元参与多能源系统运行的调度策略；对该单元各设备的备用能力进行分析，基于各设备的运行特性，提出氢能利用单元-火电联合承担备用的策略，并建立备用优化模型；最后在改进的IEEE39节点电网、20节点气网和6节点热网构成的多能源系统中进行对比仿真分析，验证所提调度方法促进高比例风光消纳和提供灵活性备用的能力。

这段摘要介绍了一个研究，其目的是解决随着风光等间歇性可再生能源大规模增长和并网所带来的问题。以下是对摘要中各部分的详细解读：

1. 问题背景：

   • 风光等间歇性可再生能源大规模增长和并网：?意味着越来越多的可再生能源，如风能和太阳能，被纳入电力系统，并且它们的产能具有间歇性。
   • 可再生能源弃能率升高与系统备用灵活性问题：?随着可再生能源的增长，由于其间歇性特性，系统中出现了可再生能源弃能的情况。同时，系统备用的灵活性也面临挑战，可能需要更好的调度方法来应对这些问题。

2. 提出的方法：

   • 高比例风光多能源系统低碳灵活调度方法：?为应对上述问题，提出了一种调度方法，重点考虑了高比例风光多能源系统的低碳和灵活性调度。

3. 研究内容和步骤：

   • 氢能综合利用单元：?针对电制氢、氢燃料电池、甲烷反应器等组成的氢能综合利用单元进行了机理分析并建模。
   • 调度策略研究：?研究了氢能综合利用单元参与多能源系统运行的调度策略。
   • 备用能力分析：?对氢能综合利用单元的各设备进行备用能力分析。
   • 联合备用策略：?基于各设备的运行特性，提出了氢能利用单元-火电联合承担备用的策略，并建立了备用优化模型。

4. 仿真验证：

   • 多能源系统仿真：?在改进的IEEE39节点电网、20节点气网和6节点热网构成的多能源系统中进行了对比仿真分析。
   • 验证调度方法的效果：?通过仿真分析验证了所提调度方法在促进高比例风光消纳和提供灵活性备用方面的效果。

综合而言，这项研究的核心目标是通过引入规模化氢能综合利用，结合高比例风光多能源系统，并采用低碳灵活调度方法，解决高比例可再生能源科学消纳与能源系统灵活稳定运行的问题。

关键词:氢能综合利用; 多能源系统；高比例风光;灵活性备用;

这些关键词涉及能源领域中的重要概念和技术，让我们分别解释它们：

1. 氢能综合利用 (Hydrogen Comprehensive Utilization):

   • 解释：?这是指对氢能源进行全面利用的过程。它可能包括从可再生能源或其他资源中生产氢气，存储氢气，并将其用于多种用途，比如作为燃料、化工原料或能源存储介质。
   • 作用：?氢能综合利用代表了一个全方位的能源利用策略，可以在能源系统中发挥多种作用，包括能源转换、储能以及作为清洁能源的一部分。

2. 多能源系统 (Multi-Energy Systems):

   • 解释：?这指的是一个能够整合和协调多种不同能源类型的系统，包括但不限于化石能源（如石油、天然气）、可再生能源（如太阳能、风能、水能）、核能等。这样的系统可以通过最佳化能源利用来提供可靠、经济和环保的能源供应。
   • 作用：?多能源系统的概念强调了能源多样化和整合，以更好地利用不同能源的优势，并在不同能源之间实现协调与平衡。

3. 高比例风光 (High Proportion of Wind and Solar):

   • 解释：?这意味着系统中风能和太阳能等可再生能源所占比例较高，可能是整个能源混合中的主要组成部分。
   • 作用：?高比例风光表示系统对于可再生能源的依赖程度较高，尤其是对风能和太阳能。这可能意味着系统面临着与这些能源相关的挑战，如不稳定性和周期性的供能。

4. 灵活性备用 (Flexibility Reserves):

   • 解释：?这是指在能源系统中，为了适应需求变化或应对能源波动性而保留的额外能力或资源。这包括可以快速调整、平衡和满足能源需求的备用措施或资源。
   • 作用：?灵活性备用是确保能源系统在面对波动需求或不稳定的可再生能源时能够保持运行稳定性和可靠性的重要因素。这包括可调度的备用发电能力或能源存储等。

综合来看，这些关键词似乎描述了一个涉及多能源整合、以高比例利用风能和太阳能为主的系统，该系统需要具备灵活性备用来应对可再生能源波动性，同时利用氢能综合利用来提供更广泛的能源转换、存储和利用方式。这些概念的综合可能是为了构建更为可持续和鲁棒的能源系统。

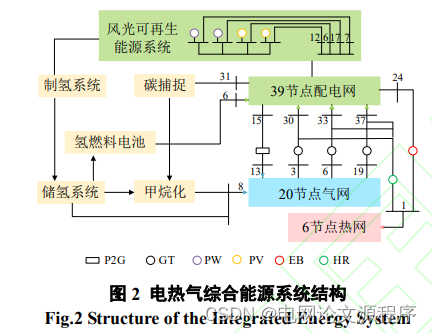
仿真算例：算例采用改进的 IEEE-39 节点的电力系统、比 利时 20 节点的天然气系统、6 节点的热力系统对所 提模型进行仿真验证，调度周期为一天 24h，步长 为1h。改进后电热气互联能源网络拓扑如图2所示。 算例给定条件如下所述： 1）多能源系统各设备、气井、天然气管道、 热网管道等运行参数、单位成本如附表 C1-C7 所 示，具体的节点连接图如附图 D1 所示，算例中典 型日负荷曲线如附图 D2 所示。2）应对可再生能源和负荷预测误差所需的旋 转备用容量按全网最大发电负荷的 5%配置。 3）在高比例风光系统中，风电装机容量为 2160MW，光伏装机容量为 2000MW，火电装机容 量为 4600MW。 4）选取单机规模 1000Nm3 /h 的电解槽，单台 功率 5MW，以 140 台并行使用，并行电解槽最大 功率 700MW。 5）选取 600 组燃料电池并行，每组额定功率 500kW，并行燃料电池最大输出功率为 300MW。 本文在计算环境 Intel Core i7-9700 CPU，16.0 GB 内存下，借助 Matlab R2018a 通过 Yalmip 工具 箱调用商用求解器 CPLEX，对含规模氢能综合利 用的高比例风光综合能源系统低碳灵活调度问题 进行求解。

仿真程序复现思路：

在这个例子中，我将考虑一个简化的能源系统优化问题，包括风光发电、储能和电力市场交易。我们将使用MATLAB，并借助YALMIP和CPLEX工具箱进行建模和求解。

function [x, objective] = modeling()
    % 定义变量
    n = 24; % 时间步数
    x = sdpvar(n, 1); % 电力输出变量
    e = sdpvar(n, 1); % 储能变量

    % 定义目标函数
    objective = sum(e); % 最小化储能成本

    % 定义约束
    constraints = [
        x <= 100, % 发电功率上限
        e >= 0,   % 储能非负
        e <= 50,  % 储能容量上限
        x + e == demand_profile() % 电力平衡约束
    ];
end
function [parameters, demand] = set_parameters()
    % 设置系统参数
    parameters.system_parameters = struct(
        'wind_capacity', 50,   % 风电容量
        'solar_capacity', 30   % 太阳能容量
    );

    % 设置电力需求
    demand = demand_profile();
end

function demand = demand_profile()
    % 模拟一天的电力需求曲线
    demand = 80 + 20 * sin(2 * pi * (1:24) / 24);
end
function main_simulation()
    % 调用参数设置
    [parameters, demand] = set_parameters();

    % 调用建模
    [x, objective] = modeling();

    % 调用 CPLEX 求解器
    options = sdpsettings('solver', 'cplex');
    optimize(constraints, objective, options);

    % 获取结果
    if (ismember('cplex', sdpsettings('solver')))
        result_power = getvalue(x);
        result_storage = getvalue(e);

        disp('Optimal Power Output:');
        disp(result_power);
        disp('Optimal Energy Storage:');
        disp(result_storage);

        % 可视化结果
        visualize_results(result_power, result_storage, demand);
    else
        disp('CPLEX not available.');
    end
end

function visualize_results(power, storage, demand)
    % 可视化仿真结果
    figure;
    subplot(2, 1, 1);
    plot(power, 'LineWidth', 2);
    hold on;
    plot(demand, '--', 'LineWidth', 2);
    legend('Power Output', 'Demand');
    xlabel('Time Step');
    ylabel('Power (MW)');
    title('Optimal Power Output vs Demand');

    subplot(2, 1, 2);
    plot(storage, 'LineWidth', 2);
    xlabel('Time Step');
    ylabel('Energy (MWh)');
    title('Optimal Energy Storage');
end
% 主程序入口
main_simulation();

在这个例子中，系统包括风力和太阳能发电，以及电力需求和储能。通过优化电力输出和储能的调度，我们可以最小化储能成本。请注意，这只是一个简单的示例，实际问题可能涉及更多的约束和复杂性。