【分治算法】之汉诺塔问题

汉诺塔问题

三根柱子 把A柱子上的盘子全部挪到C上，且每次挪动的时候 小的必须在大的上面

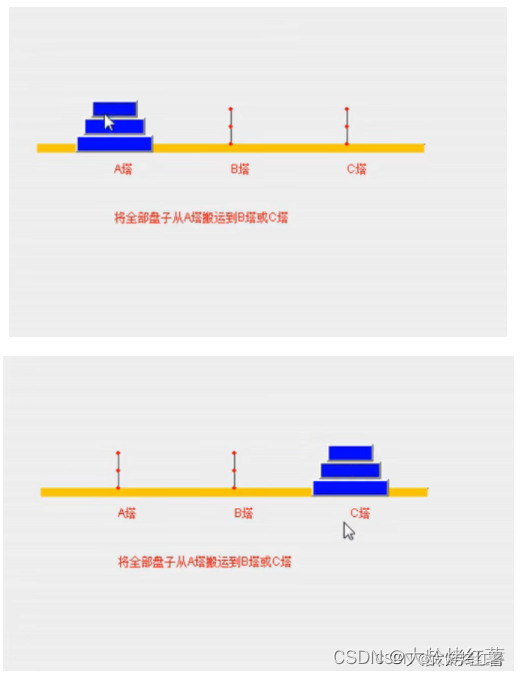
分治算法的思想;

分：把一个大问题拆成若干个小的子问题，每个子问题相互独立；

治：求解每个子问题的（递归）；

并：把子问题的解合并起来就是大问题的解；

汉诺塔拆分：

我们每次把这些个盘子看成两部分；

- 第一部分：
		最下面的一个大的作为一部分，先把他放在C上；
- 第二部分
		除去最大的剩下的整体作为一部份，再把他放在c上；
### 步骤先把第二部分移动到B上；然后第一部分就可以取出来放到C上；然后再把第二部分移动到C上；

所以剩下的就是递归解决每次拆分的两个部分即可。

package 算法.分治算法.汉诺塔问题;
//递归求解子问题
public class HanuoTower {
    // A B C  三根柱子
    public static void main(String[] args) {
            move(3,'A','B','C');
    }
    /**
     * @param num 盘的数目
     * @param a   a、b、c三根柱子
     * @param b   初始时候盘子都在A上 要把全部盘子移动到C上
     * @param c  每次移动的都是:  相应柱子最上面的盘子
     */
    public static void move(int num, char a, char b, char c) {
        //一、如果只有一个盘 则从A—>C
        if (num==1){
            System.out.println(a+"—>"+c);
        }else {
        //二、盘子数目>=2，我们每次把盘子看成2部分，最下面的一个盘 1，和上面剩余的部分num-1
            //此时分三步走
            //1.先把A上面的所有盘子从A—>B 上面所有的盘子数量为num-1；
                //递归把盘子从A—>B  我们需要借助中间盘C盘 所以C放在中间
            move(num-1,a,c,b);
            //2.把最下面的盘子从A—>C
            System.out.println(a+"—>"+c);
            //3.把B上的盘子从B—>C
                //刚才把第一部分的num-1个盘子从A—>B，所以B->C也是num-1个 借助A盘，所以A放中间
            move(num-1,b,a,c);
        }
    }
}

**简化的思想：
//目的：把a上的盘子挪到c上
public class Main {
    public static void main(String[] args) {
        move(5, 'A', 'B', 'C');
    }
    public static void move(int n, char a, char b, char c) {
        //分两种情况 一只有一个盘子； 二很多盘子
        //一、n==1
        if (n == 1) {
            System.out.println(a + "->" + c);
        } else {
            //二、n>=2  三步走
            //①把上面的n-1个盘子，从a放到b上，c做媒介
            move(n - 1, a, c, b);
            //②把最下面的这个一个盘子从a直接放到c上
            System.out.println(a + "->" + c);
            //③再把b上的n-1个盘子，从b放到c上，a做媒介
            move(n - 1, b, a, c);
        }
    }
}