论文速看 A Closer Look at Few-shot Image Generation

A Closer Look at Few-shot Image Generation

Year:2022
Paper link: link
Github link: link(seems like offical)

Abstract

1. As our first contribution, we propose a framework to analyze existing methods during the adaptation.
   Our analysis discovers that while some methods have disproportionate focus on diversity preserving which impede quality improvement, all methods achieve similar quality after convergence .
   Therefore, the better methods are those that can slow down diversity degradation. Furthermore, our analysis reveals that there is still plenty of room to further slow down diversity degradation.
2. Informed by our analysis and to slow down the diversity degradation of the target generator during adaptation, our second contribution proposes to apply mutual information(MI) maximization to retain the source domain’s rich multi-level diversity information in the target domain generator.
   We propose to perform MI maximization by contrastive loss (CL), leverage the generator and discriminator as two feature encoders to extract different multi-level features for computing CL.
   We refer to our method as Dual Contrastive Learning (DCL).
   

Introduction

This few-shot image generation task is important in many real-world applications with limited data, e.g., artistic domains. It can also benefit some downstream tasks, e.g., few-shot image classification.

A Closer Look at Few-shot Image Generation

The early method is based on fine-tuning [49]. In particular, starting from the pretrained generator $G_S$, the original GAN loss [15] is used to adapt the generator to the new domain:
$$\underset{G_t}{\min }\underset{D_t}{\max }=E_{x～p_{data}(x)}[\log D_t(x)]+E_{z～p_z(z)}[\log (1?D_t(G_t(z)))]\text{\hspace{1em}(1)}$$
$G_t$ and $D_t$ are generator and discriminator of the target domain, and $G_t$ is initialized by the weights of $G_s$.This GAN loss in Eqn. 1 forces Gt to capture the statistics of the target domain data, thereby to achieve both good quality(realisticness w.r.t. target domain data) and diversity, the criteria for a good generator.
However, for few-shot setup (e.g. only 10 target domain images), such approach is inadequate to achieve diverse target image generation as very limited samples are provided to define $p_{data}(x)$
In [34], an additional Cross-domain Correspondence (CDC) loss is introduced to preserve the sample-wise distance information of source to maintain diversity, and the whole model is trained via a multi-task loss with the diversity loss $L_{dist}$ as an auxiliary task to regularize the main GAN task with loss $L_{adv}$:
$$\underset{G_t}{\min }\underset{D_t}{\max }{L}_{adv}+L_{dist}\text{\hspace{1em}(2)}$$
In [34], a patch discriminator [21, 61] is also used to further improve the performance in $L_{a}dv$. Details of $L_{d}ist$ in [34].

questions

1. With disproportionate focus on diversity preserving in recent works [29,34], will quality of the generated samples be compromised? For example, in Eqn. 2, $L_{adv}$ is responsible for quality improvement during adaptation, but $L_{dist}$ may compete with $L_{adv}$ as it has been observed in multi-task learning[13, 41]. We note that this has not been analyzed thoroughly.
2. With recent works’ strong focus on diversity preserving [29, 34], will there still be room to further improve via diversity preserving? How could we know when the gain of diversity preserving approaches become saturated(without excessive trial and error)?(Wow!)

[13] Christopher Fifty, Ehsan Amid, Zhe Zhao, Tianhe Yu, Rohan Anil, and Chelsea Finn. Measuring and harnessing transference in multi-task learning. arXiv preprint arXiv:2010.15413, 2020. 2, 5.
[41] Trevor Standley, Amir Zamir, Dawn Chen, Leonidas Guibas, Jitendra Malik, and Silvio Savarese. Which tasks should be learned together in multi-task learning? In International Conference on Machine Learning, pages 9120–9132. PMLR, 2020. 2, 5.

Contributions

1. we propose to independently analyze the quality and diversity during the adaptation.
   Insightful information: In particular, on one hand, it is true that strong diversity preserving methods such as [34]indeed impede the progress of quality improvement.
   On the other hand, interestingly, we observe that these methods can still reach high quality rather quickly, and after quality converges they have no worse quality compared to other methods such as [49] which uses simple GAN loss (Eqn. 1).
   Therefore, methods with disproportionate focus on preserving diversity [34] stand out from the rests as they can produce slow diversity-degrading generators, maintaining good diversity of generated images when their quality reaches the convergence.
   Furthermore, our analysis reveals that there is still plenty of room(really) to further slow down the diversity degradation across several source$\to$target domain setups.
2. Informed by our analysis, our second contribution is to propose a novel strong regularization to take a further step in slowing down the diversity degradation, with the understanding that it is unlikely to compromise quality as observed in our analysis.
   We present a simple and novel method via contrastive loss. We hypothesize that, the same noise input could be mapped to fake images in the source and target domains with shared semantic information.
   Our proposed regularization is based on the observation that rich diversity exists in the source images at different semantic levels: diversity in middle levels such as hair style, face shape, and that in high levels such as facial expression(smile, grin, concentration)
   However, such source diversity can be easily ignored in the images produced by target domain generators.
   Therefore, to preserve source diversity information, we propose to maximize the mutual information(MI) between the source/target image features originated from the same latent code, via contrastive loss[35] .
   To compute CL, we leverage the generator and discriminator as two feature encoders to extract image features(How) at multiple feature scales, such that we can preserve diversity at various levels.

[49] YaxingWang, ChenshenWu, Luis Herranz, Joost van deWeijer, Abel Gonzalez-Garcia, and Bogdan Raducanu. Transferring gans: generating images from limited data. In Proceedings of the European Conference on Computer Vision (ECCV), pages 218–234, 2018. 2, 3, 5, 6, 14
[35] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748, 2018. 2, 3, 5, 6, 13

what I get

1. A new way to evaluate the quality during adaptation by using a trained binary classifier. But for the target domain which can not collect enough data, this way do not work.
2. A brilliant and which I think it is right, is the best model is which can slow down the diversity degradation, and more precisely the best model is the counter where the good quality catch the slowly down’s diversity. And I think it is a new point of view to analyze the whole question.
   We observe that, most of existing methods lose diversity quickly before the quality improvement converges, and tend to replicate the training data.(So clearly the best model was the one which maintain diversity after or when the quality improve converges)
3. A new method to preserve diversity using the so-called DCL(Dual contrastive learning) to maximize the MI(mutual information), and I am curious about the details. a simple thought is that I think maybe the method is a little complicate.
4. Respect for the authors for such a paper.

Questions

1. we see from the results, the method of preserving diversity will slow down the progress of quality during adaptation, but compare with this little effect, we see more gain on the diversity of the results during adaption.

Related work

Baseline mentioned

Baseline models	brief sum
BSA [33]	only update the learnable scale and shift parameters of the generator during adaptation;
FreezeD [32]	freeze a few high-resolution layers of thediscriminator, during the adaptation process;
MineGAN [48]	use additional modules between the noise input and the generator. It aims at matching the target distribution before input to the generator;
Elastic Weight Consolidation (EWC) [29]	apply EWC loss to regularize GAN, preventing the important weights from drastic changes during adaptation;
Cross-domain Correspondence (CDC) [34]	preservethe distance between different instances in the source.

Contrastive learning

Our proposed method is related to contrastive learning[5, 9, 16, 18, 35, 57].Contrastive learning for unsupervised instance discrimination aims at learning invariant embeddings with different transformation functions of the same object [18, 22, 31], which can benefit the downstream tasks.

Revisit Few-shot GAN adaptation

Binary classification for Quality Evaluation

we employ the probability output of a binary classifier to assess to what extent the generated images belong to the target domain.
7. In particular, we train a convolutional network $C$ on two sets of real images (from source and target, excluded during adaptation).
8. Then, we apply $C$ to the synthetic images from the adapted generator $G_t$ during adaptation. The soft output of $C$ are $p_t$, predicted probability of input belonging to the target domain, and $(1?p_t)$, that of not belonging to the target domain. Therefore, we take $p_t$ as an assessment of the realisticness of the synthetic images on the target domain:
$$p_t=E_{z～p_z(z)}[C(G_t(z))]\text{\hspace{1em}(3)}$$
$z$ is a batch of random noise input (size=1,000) fixed during adaptation, which is a proxy to indicate the quality and realisticness evolution process of different methods.

Intra-Cluster Diversity Evaluation

The standard LPIPS evaluates the perceptual distance between two images, and it is empirically shown to align with human judgements.
Intra-LPIPS is a variation of the standard LPIPS.
-> We firstly generate abundant(size=1,000) images
-> assign each of them to one of the M target samples (with lowest standard LPIPS) and form M clusters.
-> computing the average standard LPIPS for random paired images within each cluster, then average over M clusters.

Ideally, we hypothesize that the highest diversity knowledge is achieved by the generator pretrained on the large source domain, and it will degrade during the few-shot adaptation. In the worst case, the adapted generator simply replicates the target images, and intra-LPIPS will be zero.

Empirical Analysis Results

Image quality\realisticness

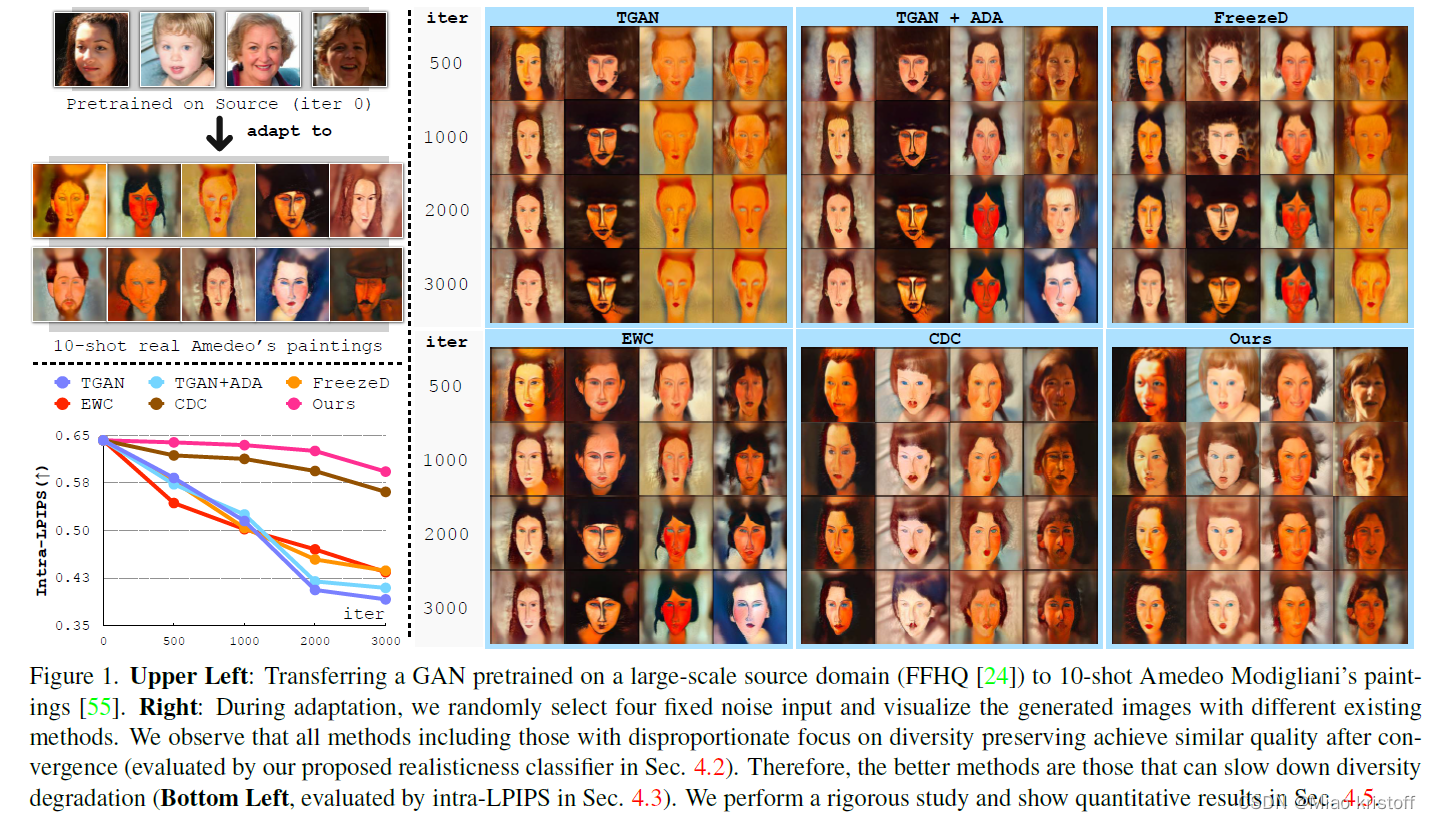
As shown in below Figure, strong diversity preserving methods such as CDC [34] (and ours, to be discussed in Sec. 5) indeed impede the progress of quality improvement, most noticeable in FFHQ $\to$ Babies. This is because additional regularization for diversity preserving (e.g. $L_{dist}$ in [34], see Eqn. 2) competes with main GAN loss $L_{adv}$ which is responsible for quality improvement. On the other hand, interestingly, we observe that these methods can still reach high quality on the target domain rather quickly, and they achieve similar quality as other methods after quality converges.
We conjecture that, due to the informative prior knowledge on the source domain, it is not difficult to obtain adequate realisticness when transferring to the small target domain.

Observation 1: While methods such as CDC [34] have disproportionate focus on diversity preserving which impedes quality improvement, all methods we have evaluated achieve similar quality/realisticness after convergence.

Image diversity

As shown in Figure 2b, for all existing methods, the loss of diversity is inevitable in adaptation.
On the other hand, since all methods achieve similar realisticness after the quality converges, the better generators are those that can slow down the diversity degradation, and the worse ones are those that lose diversity rapidly before the convergence of the quality improvement.
Recalling the concerns we raise we show that, there is still plenty of room to further reduce the rate of diversity degradation,
besides, the gain of diversity preservation becomes saturated only until the rate of diversity degradation is much reduced.(i do not understand)

Observation 2: Different methods exhibit substantially dissimilar diversity degrading rates. Combined the results in Figure 2a and 2b: since the achieved quality is similar, the better methods are those that can slow down diversity degradation.

Dual Contrastive Learning

Rich diversity exists in the source images $G_S(z)$ at different semantic levels:
To preserve source images’ diversity information in the target domain generator, we propose to maximize the mutual information(MI) between the source/target image features originated from the same input noise.
In particular, for an input noise $z_i$, we seek to maximize:
$$MI({\pi }^l(G_t(z_i));{\pi }^l(G_s(z_i)))\text{\hspace{1em}(4)}$$
and ${\pi }^l(?)$ is a feature encoder to extract l-th level features.
Furthermore, in GAN, we have $G_t$ and $D_t$, and we take advantage both of them to use as the feature encoders ${\pi }^l(?)$ to extract different features. As directly maximizing MI is challenging [37], we apply contrastive learning[35] to solve Eqn. 4.

Dual Contrastive Learning

There are several goals for DCL

1. Maximize the MI between generated images on the source/target domain originated from the same noise input.
2. push away the generated images on the source and target domain that use different noise input.
3. push away the generated target images and the real target images, to prevent collapsing to the few-shot target set.

To achieve these goals, we let the generating and the discriminating views using the same noise input, on source and target, as the positive pair, and maximize the agreement between them.

Concretely, DCL includes two parts.

Generator CL

Given a batch of noise input { z 0 , z 1 , ? ? , z N ? 1 } {\{z_0,z_1, \cdots, z_{N-1}\}} {z0?,z1?,?,zN?1?}, we obtain images { G s ( z 0 ) , G s ( z 1 ) , ? ? , G s ( z N ? 1 ) } \{G_s(z_0),G_s(z_1),\cdots,G_s(z_{N-1})\} {Gs?(z0?),Gs?(z1?),?,Gs?(zN?1?)} and { G t ( z 0 ) , G t ( z 1 ) , ? ? , G t ( z N ? 1 ) } \{G_t(z_0),G_t(z_1),\cdots, G_t(z_{N-1})\} {Gt?(z0?),Gt?(z1?),?,Gt?(zN?1?)}, generated on the source and the target domain, respectively.
Considering an anchor image $G_t(z_i)$(just make it an anchor image), we optimize the following object:
$$L_{C{L}_1}=?log\frac{f(G_t^l(z_i),G_s^l(z_i))}{{\sum }_{j=0}^{N?1}f(G_t^l(z_i),G_s^l(z_j))}\text{\hspace{1em}(5)}$$
which is an N-Way categorical cross-entropy loss to classify the positive pair $(G_t^l(z_i),G_s^l(z_j))$ at l-th layer correctly. $\frac{f(G_t^l(z_i),G_sl(z_i))}{\sum^{{N-1}_{j=0}f(G_t}l(z_i),G_s^l(z_j))}$is the prediction probability and
$$f(G_t^l(z_i),G_s^l(z_i))=exp(CosSim(G_t^l(z_i),G_s^l(z_i))/\tau )\text{\hspace{1em}(6)}$$ for i ∈ { 0 , 1 , ? ? , N ? 1 } i\in\{0,1,\cdots,N-1\} i∈{0,1,?,N?1} is the exponential of the cosine similarity between l-th layer features of the generated images on source and target, scaled by a hyperprameter temperature $\tau =0.07$ and passed as logits [18, 38].

Discriminator CL

We focus on the view of the discriminator $D_t$.
-> Given the generated images by the source and target generator and real data $x$ as input to $D_t$, we maximize the agreement between the discriminating features of the generated images on source and target, using the same noise $z_i$.
-> To prevent replicating the target data, we regularize the training process by pushing away discriminating features of the generated target images and the real target data at different scales.
$$L_{C{L}_2}=?log\frac{f(D_t^l(G_t(z_i)),D_t^l(G_s(z_i)))}{f(D_t^l(G_t(z_i)),D_t^l(G_s(z_i)))+\Delta }\text{\hspace{1em}(7)}$$
where $\Delta ={\sum }_{j=1}^{M}f(D_t^l(G_t(z_i)),D_t^l(x_j))$ and $M$ is the number of real target images. The final objective of DCL in our work is simply:
$$\underset{G}{\min }\underset{D}{\max }{L}_{adv}+{\lambda }_1{L}_{CL1}+{\lambda }_2{L}_{CL2}\text{\hspace{1em}(8)}$$
In practice, we find ${\lambda }_1=2$ and ${\lambda }_2=0.5$ work well. In each iteration, we randomly select different layers of $G_t$ and $D_t$ to perform DCL with multi-level features.

Design choice

Our idea is to re-use the highest diversity knowledge from the source as the strong regularization to slow down the inevitable diversity degradation, before the quality improvement converges.
Differently, Discriminator CL regularizes the adversarial training: while fitting to the target domain, the generated target images are encouraged to be pushed away from the real data at different feature scales.
Under mild assumptions, DCL maximizes the MI (Eqn.4) between the generated samples using the same input noise, on source and target, e.g., for $L_{C{L}_1}:MI(G_t^l(z_i);G_s^l(z_i))\ge \log [N]?L_{C{L}_1}$.(why this)

Experiments

Qualitative results

Basic setups: We mostly follow the experiment setups as Ojha et al. [34], including the non-saturating GAN loss $L_{adv}$ in Eqn. 2, the same pretrained GAN and 10-shot target samples, with no access to the source data. We employ StyleGAN-V2 [25] as the GAN architecture for pretraining and few-shot adaptation, with an image/patch level discriminator[34].

We observe that, most of existing methods lose diversity quickly before the quality improvement converges, and tend to replicate the training data.
Our method, in contrast, slows down the loss of diversity and preserves more details. In red frames (Upper), the hair style and hat are better preserved.

In pink frames (Bottom), the smile teeth are well inherited from the source domain. We also outperform others in quantitative evaluation (Right).

Quantitative comparison

We mainly focus on two metrics to evaluate our method. 1) For datasets which contain a lot of real data, e.g., FFHQ-Babies, FFHQ-Sunglasses, we apply the widely used Frechet Inception Distance (FID) [19] to evaluate the generated fake images.
2) For those datasets which contain only few-shot real data, FID becomes tricky and unstable, since it summarizes the quality and diversity to a single score. Therefore, we use intra-LPIPS (see Sec. 4.3) to measure the diversity of generated images. The better diversity comes with a higher score.

As shown in the above tables, our method outperforms the baseline methods. This indicates that the target generator we obtain can cover a wide range of modes, and the loss of diversity is further reduced.

Effect of the binary of classifier

The goal of our proposed binary classifier is to detect if an input image is “non-target” or “target”. In Figure 6 (left), we replace the source with equally sampled images from FFHQ, ImageNet [10], CUB [45], Cars [27]g as “non-target” and Sketches as “target”, and we observe the similar results, compared to Figure 2a.

Ablation of the realisticness classifier. We show that 1): Using alternative datasets as non-target to train the classifier give similar results. 2): Moreover, if we input randomly generated noise images, the classifier will give low confidence of being target.

Ablation study of DCL

We also show that both Generator CL and Discriminator CL can slow down the diversity degradation, and the better results are achieved when combined together.

Effect of target data size

do not know

contrastive learning
LPIPS [58] Richard Zhang, Phillip Isola, Alexei A Efros, Eli Shechtman, and OliverWang. The unreasonable effectiveness of deep features as a perceptual metric. In CVPR, 2018. 3, 4, 14
multi-task learning Note that such observation is consistent with findings in multi-task learning [13,41]

• [13] Christopher Fifty, Ehsan Amid, Zhe Zhao, Tianhe Yu, Rohan Anil, and Chelsea Finn. Measuring and harnessing transference in multi-task learning. arXiv preprint arXiv:2010.15413,2020. 2, 5*
  [41] Trevor Standley, Amir Zamir, Dawn Chen, Leonidas Guibas, Jitendra Malik, and Silvio Savarese. Which tasks should be learned together in multi-task learning? In International Conference on Machine Learning, pages 9120–9132. PMLR,2020. 2, 5

patch discriminator

words

impede阻止
disproportionate不成比例的
compromised妥协
decouple使分开
exclude不包括，排除
empirically以观察或实验为证据的
conjecture推测
mild温和的