【硕士论文复现】可再生能源发电与电动汽车的协同调度策略研究(Matlab代码实现)
?💥💥💞💞欢迎来到本博客????💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
??座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
文献来源:



1.1 上层问题
在第3章所建立的上层模型中,目标函数为二次凸函数,且约束条件均为线性,属于典型的二次规划问题,二次规划问题是最基本的非线性规划问题,其主要特点就是目标函数为二次型且约束均为线性约束,一般形式可以表示如下:
?1.2 下层问题
下层对各充电站有功无功充放量以及各可再生能源发电站无功出力的优化过程,实际上就是调度对象仅包含电动汽车储能和可再生能源的配电网的有功无功协调优化过程,属于最优潮流问题。最优潮流的求解方法主要分为智能算法和数值分析法两大类。智能算法对问题的形式没有任何要求,具有极强的通用性,并且从理论上具有全局寻优的能力。但在实际应用中,该类算法容易陷入局部最优,而且存在计算量大,寻优速度慢,求解结果不稳定等弊端[42]。
本文提出的调度策略是实时进行的,具有一定的计算速度的要求,从而也限制了对智能算法的使用。数值分析法大都只具备局部寻优能力,只有凸规划方法具有全局寻优性。此外,下层模型中计及充电桩及可再生能源并网逆变器的无功响应,配电网的运行优化过程涉及有功及无功的协调优化,该模型中的最优潮流问题是一个非凸非线性问题,基于凸优化理论的凸规划能够通过在算法上进行松弛为非凸问题提供一个有效的解决途径。
目前,凸优化算法中的半正定规划(semi-definite programming, SDP)和二阶锥规划(second order conic programming, SOCP)在电力系统中的应用较为广泛,其中SOCR作为锥规划中的一个特例,使用和求解较其他锥规划更加容易,因此对SOCR 的研究和应用也最为广泛。
二阶锥规划作为一种凸优化,拥有凸规划的所有优势,因此在二阶锥规划问题中,所有的局部最优解都是全局最优的,且求解效率及准确性相较于非线性规划有了明显提高。但它要求优化模型的目标函数必须为线性43,因此在下层模型的目标函数中,使用支路电流描述系统的有功网损,即可将原目标函数转换为线性函数:
详细讲解见第4部分。?
📚2 运行结果
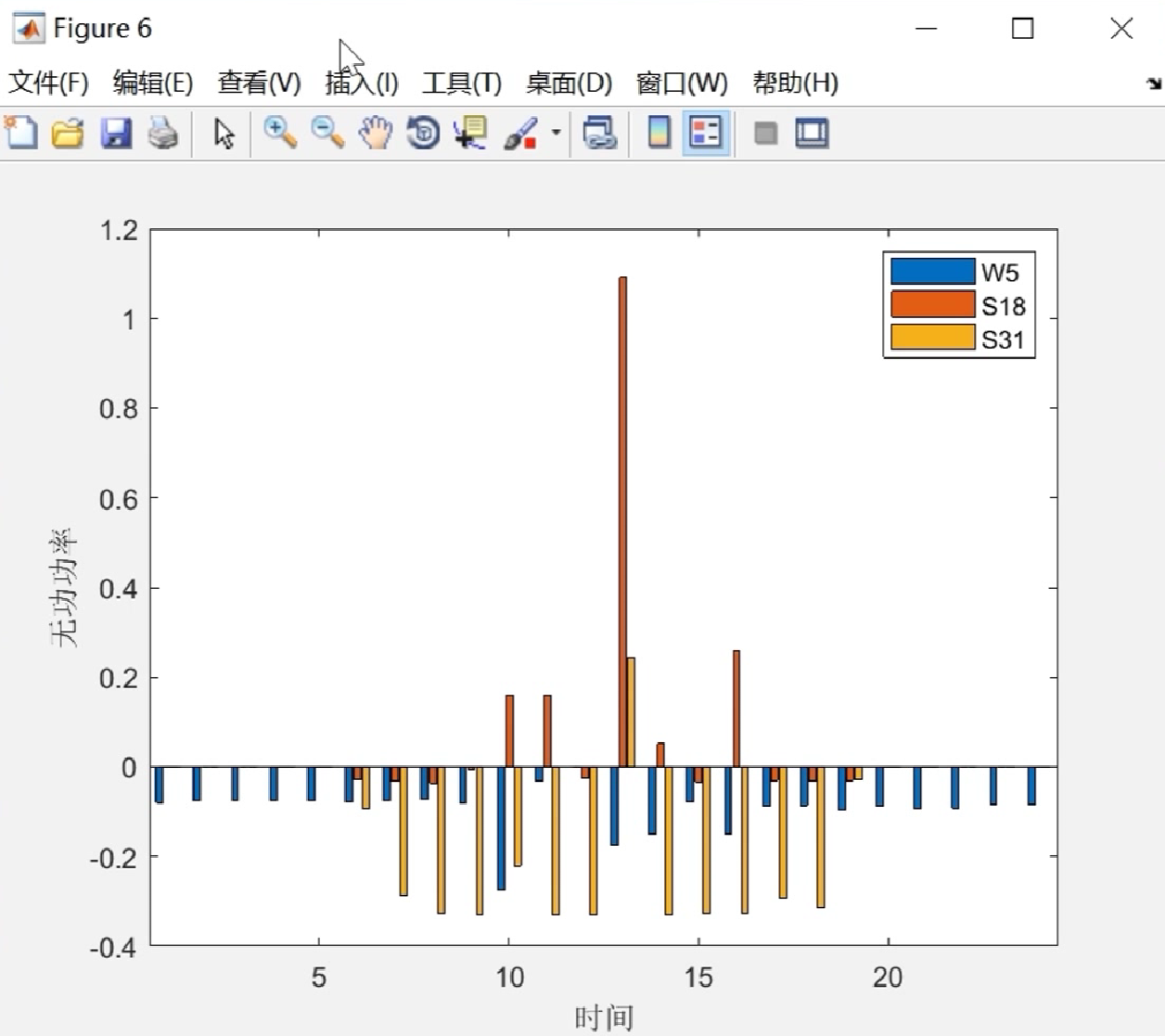

 ?
?
部分代码:
%% 1.设参
mpc = IEEE33BW;
pload = mpc.Pload(:,t)*(pload1(t)/sum(mpc.Pload(:,t)))/100;%节点有功负荷
qload = mpc.Qload(:,1);%节点无功负荷
branch = mpc.branch_CG(1:32,:);
branch(:,3) = branch(:,3)*100/(12.66^2);%求阻抗标幺值
r=real(branch(:,3));
x=imag(branch(:,3));
r=r(1:32);
x=x(1:32);
T = 1;%时段数为1小时
nb = 33;%节点数,根节点为33
nl = 32;%支路数
nc = 5;%联络开关数
upstream=zeros(nb,nl);%代表流入节点支路
dnstream=zeros(nb,nl);%代表流出节点支路
for i=1:32
? ? upstream(i,i)=1;
end
% upstream(20,33)=1;%支路33为20-7支路,流入节点20
% upstream(14,34)=1;%支路34为14-8支路,流入节点14
% upstream(21,35)=1;%支路35为21-11支路,流入节点21
% upstream(32,36)=1;%支路36为32-17支路,流入节点32
% upstream(28,37)=1;%支路37为28-24支路,流入节点28
🎉3?参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]赵浩然. 可再生能源发电与电动汽车的协同调度策略研究[D].山东大学,2020.DOI:10.27272/d.cnki.gshdu.2020.001215.
🌈4 Matlab代码、数据
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Linux的权限(2)
- echarts柱状图多系列两两重叠
- Spring中的@Resource/@Autowired/@Primary/@Qualifier
- 【笔记------freemodbus】一、stm32的裸机modbus-RTU从机移植(HAL库)
- 陪护系统|陪护系统的设计原理与技术实现
- 消除代码冗长神器 - Lombok | val/var 本地变量声明
- SDG大数据平台简介
- 基于SSM的智慧教室管理系统的设计与实现+63375(免费领源码)可做计算机毕业设计JAVA、PHP、爬虫、APP、小程序、C#、C++、python、数据可视化、大数据、全套文案
- 2023年四川网信人才技能大赛 决赛 实操赛Web ezbbs Writeup
- 【计算机组成原理】总复习笔记(上)