数据结构学习笔记——查找算法中的树形查找(红黑树)
一、红黑树的定义
红黑树是一棵二叉排序树(满足结点值中:左子树<根结点<右子树),每个结点都带有颜色属性,即黑或红。可以简单地说它是一棵“ 平衡二叉树 ”,但由于它的左、右子树高度差的绝对值有可能超过 1,所以并不是严格意义上的平衡二叉树,只能说是一棵弱平衡二叉树,相对于正常的平衡二叉树,在进行插入、删除操作后二叉树的平衡调整中由于不要求完全平衡,其所需的代价更低。
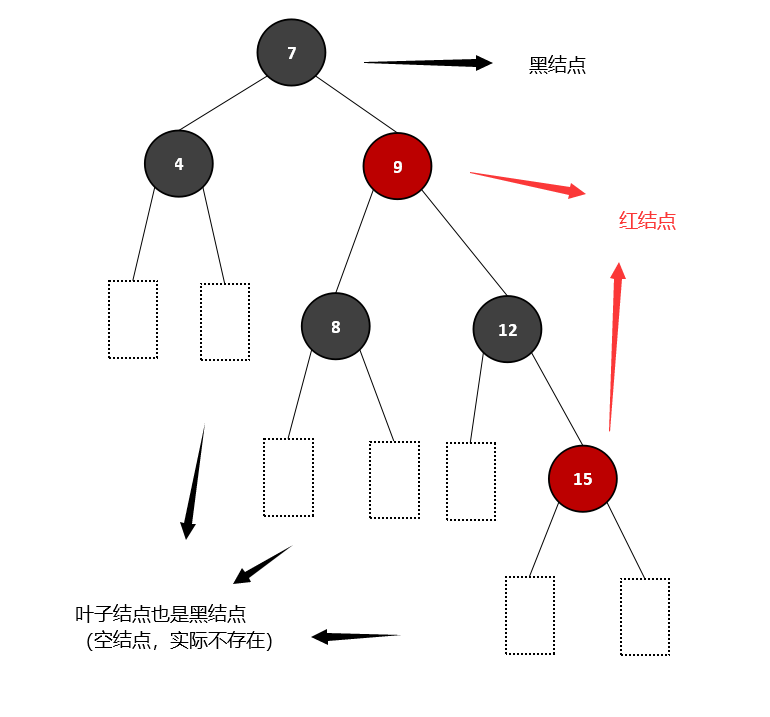
(一)黑/红结点、叶子节点
在红黑树中,根结点一定是黑结点,其余结点为黑或红,树中不允许有相邻的两个红结点;另外,树中也存在叶子结点,它是黑结点,是实际意义上不存在的空结点,且任一结点(不包括)到叶子结点的路径上,所经过的黑结点的个数相同,注意叶子结点也算作黑结点计入。
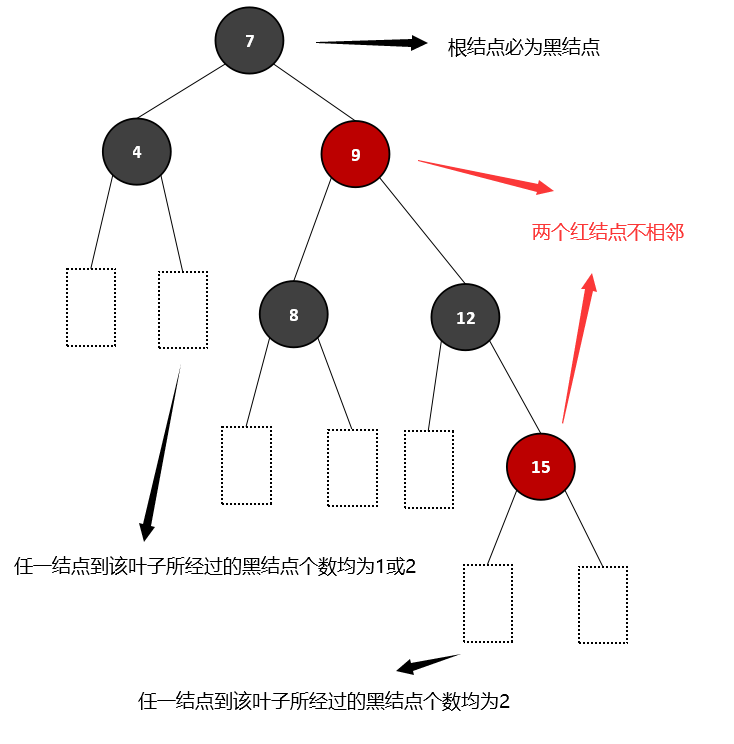
(二)黑色完美平衡
若红黑树中,左子树和右子树的层数相等,则称为黑色完美平衡,如下:
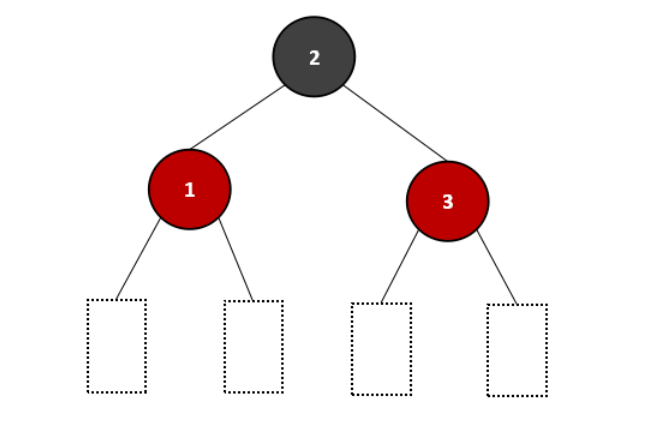
二、红黑树的性质
(一)黑高和高度
任意一结点(不包括)到叶子结点所经过的黑结点的个数称为该结点的黑高,而根结点的黑高即为红黑树的高度,黑高用bh表示,例如,下图这棵红黑树的高度即为根结点3的黑高,即bh=2:
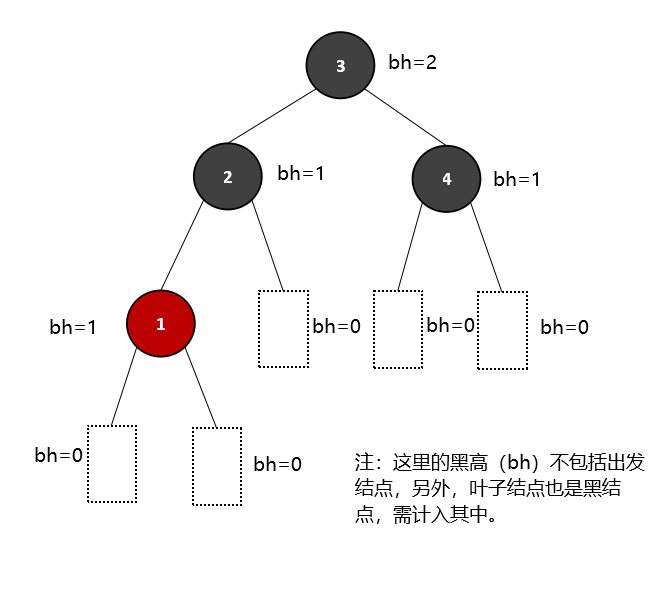
由于根结点到叶子结点的最长路径不大于最短路径的两倍,且至少有一半结点为黑结点,即树的黑高至少为h/2,所以对于一个含有n个结点的红黑树,其高度为h ≤ 2log2(n+1),即最大高度为2log2(n+1)。
(二)叶子结点个数
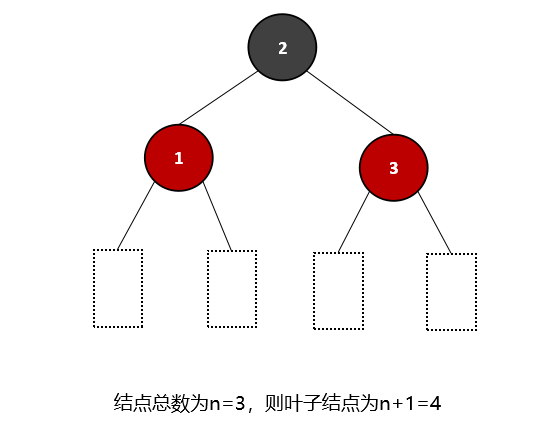
红黑树中,叶子结点(空结点)与二分判定树和B树中的外部结点相同,都不是实际存在的结点,是虚构的。若红黑树的结点总数为n,则外部结点的个数为n+1。
三、红黑树与AVL对比
与平衡二叉树(AVL)相比,红黑树只追求大致上的平衡,通过引入红、黑颜色属性以及相应的规则来保证平衡性,所以红黑树在插入和删除结点时只需进行少量的颜色调整和旋转操作,从而比AVL实现更简便,而AVL必须遵从严格的平衡条件,使得在进行插入和删除结点操作后需要多次旋转调整来保证平衡,可能会增加操作的时间复杂度。另外,AVL与红黑树相同,两者查找、插入和删除操作的时间复杂度均为O(log2n)。
由于每一棵红黑树都是一颗二叉排序树,因此,在对红黑树进行查找时,可以采用运用于普通二叉排序树上的查找算法,在查找过程中不需要颜色信息。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【DDR】基于Verilog的DDR控制器的简单实现(二)——写操作
- 【CPP】随手记
- Python知识点(3)
- 面试算法105:最大的岛屿
- 【电路电子学】7天速通攻略+笔记
- Java_集合进阶Map实现类
- Android 10.0 内置google tts语音包功能实现
- 数字化校园实验室综合管理平台|推动实验室创新发展新引擎
- APP加固技术及其应用
- 实习知识整理7:SpringBoot和html+thymeleaf模板的项目的相关配置文件