过采样技术基本原理

本文介绍过采样技术基本原理。

过采样技术在ADC信号采集过程中使用还是比较多的。某些使用场景下，对采样速度要求并不是那么高（或ADC采样速度过剩），但是想要获取较高的分辨率，就会用到这种技术，如针对温度，压力等缓慢变化的传感器信号采集。过采样技术是典型的以牺牲采样速度换取有效分辨率的方法。

1.基本概念

1)适用范围：

采用过采样技术提高ADC分辨率，需满足以下条件：

a)输入信号有白噪声，且其功率均匀分布在我们感兴趣的频段

b)噪声需随输入信号变化的幅度超过1个LSB（也即测量输入信号抖动大于1个LSB），如果不超过1LSB，过采样提升有效位数没有意义

2)信噪比（SNR）

对于ADC而言，当输入信号是一个满量程的正弦信号，其信噪比（SNR）最大，有：

其中，N为ADC的分辨率。我们对N求导，可得：d(SNRdB)/d(N)=6.02，也就是说，1个bit的分辨率对应6.02dB的信噪比（SNR），提高了信噪比（SNR）就可以增加ADC的分辨率。这也是过采样技术的核心。

3)采样定理

采样定理从理论上指明了要想重建输入的模拟信号，采样频率fs必须大于等于输入模拟信号最高频率fm的2倍。即：

fsfm*2

其中，fs为采样频率，fm为输入模拟信号最高频率

否则，信号会发生混叠，这也是为什么在ADC前端加抗混叠滤波器的原因。

4)过采样

假设量化噪声为白噪声，且其功率密度均匀的分布在直流和采样频率之间，白噪声与采样频率不相关。当提高采样率后，量化噪声被平均到整个采样频率段内，如下图所示。

从图中可知，量化噪声功率分布的频率被扩展到采样频率fs（大于fm），超过fm的这段可以通过数字低通滤波器极大的削弱。整个过程造成的结果是噪声减少了，进而信噪比（SNR）提高了，再进而有效位数增加了。经过公式推导（这里不详述，可参考其它资料），可得，

N为ADC的分辨率，OSR为过采样率，比较2)中的公式，其信噪比（SNR）增加了10log(OSR)，假设OSR=2，则10log(OSR)=3，即信噪比（SNR）增加了3dB（前面讲过，信噪比（SNR）每增加6dB，有效位数增加1bit），有效位数增加1/2bit。这里，我们可以得出OSR每增加4倍，有效位数加1bit，即：

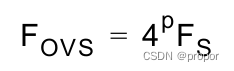
其中，FS为当前ADC的采样频率

5)抽取

由于增加了采样频率，我们采样的数据量也增加了，而我们实际上使用的采样率还是FS，而非FOVS（提高采样率并非我们的本义，我们是想要提高有效位数）。因此，需要对数据进行抽取，以获得我们增加了有效位数的ADC值。简单来讲，抽取就干2件事：

a)降采样，FOVS变为FS

b)对数据进行处理，获得增加了有效位数的ADC值

针对a)，我们可以连续采样个采样值（按FOVS采样），数据处理后，输出一个值，即可将采样率变为FS。

针对b)，由于我们采用过采样，采样频率是原来的倍，采样值数量也为原来的倍，假设原采样频率，Ts后得到一个样本值s，过采样频率得到的样本值求和为*s，增加的有效位数为log2(*s)-log2(s)=2p，若原来的有效位数为N，则过采样频率得到的样本值求和后的样本值有效位数为N+2p，为了获得p位有效位数，需要右移p位（N+p+p-p），即可得到N+p的有效位数。

2.实施

1)若想增加p bit的有效位数，需将原来采样频率FS提升为：*FS，当然ADC的采样频率是有最大值的，注意不要超过最大频率。

2)连续采样个值，对其进行求和，右移p位，此值即为过采样后的值。这一步可以配合定时器（固定FS触发ADC采样），中断，DMA进行处理以提高CPU使用效率。

总结，本文介绍了过采样技术基本原理。