数学建模算法0基础学习第五天-插值算法

一、前言

常常需要根据已知的函数点进行数据、模型的处理和分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就 需要使用一些数学的方法，“模拟产生”一些新的但又比较靠谱的值来满 足需求，这就是插值的作用。

本次将通过介绍五种插值算法，并举例说明。

二、插值类别

拉格朗日插值法，牛顿插值法，埃尔米特插值法，分段线性插值法、三次样条插值法

2.1拉格朗日插值法

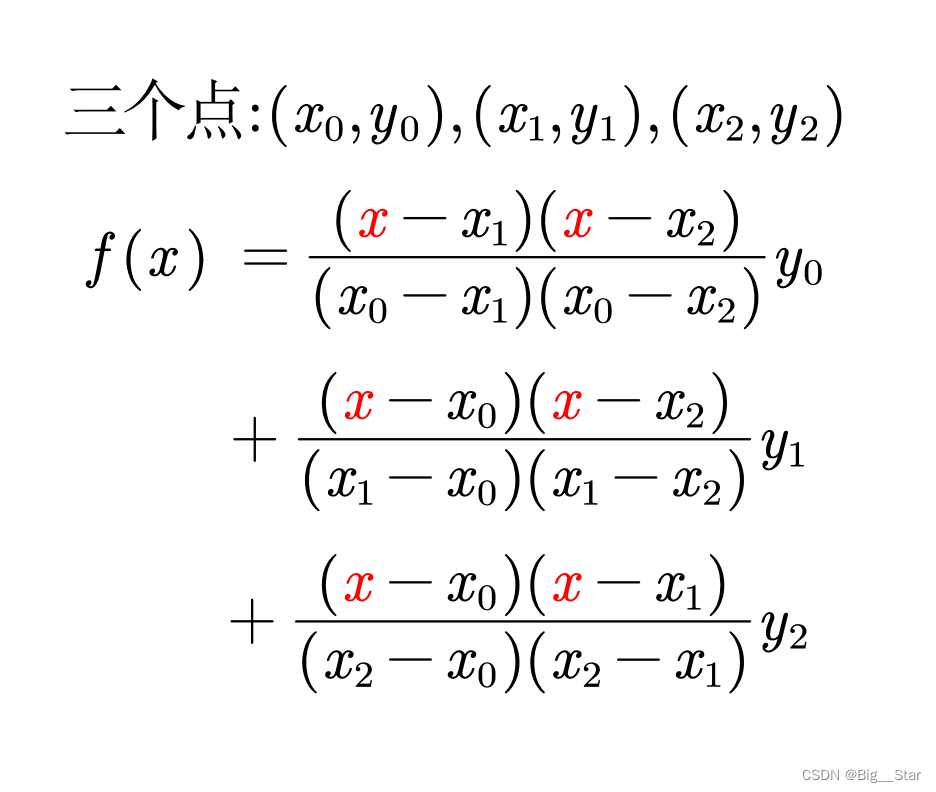
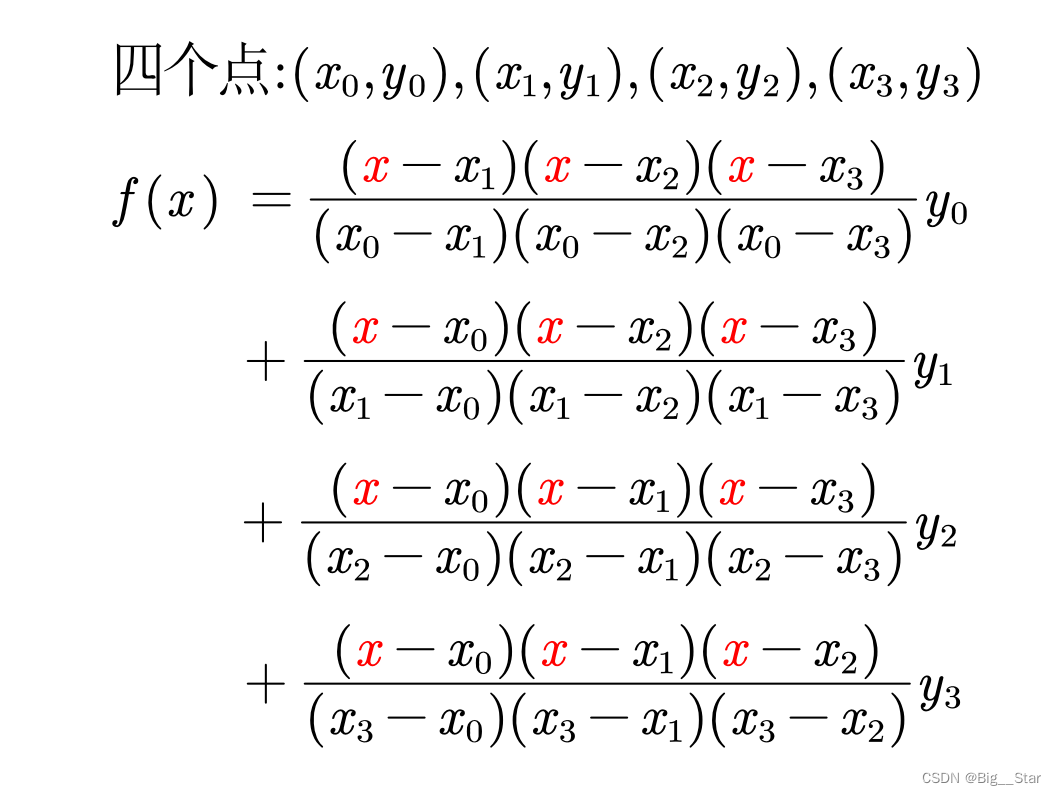
拉格朗日是n次多项式插值，解题方法是先构造插值基函数再求n次插值多项式。对Lagrange n次插值多项式，首先要选取n+1个插值点上的次插值基函数。

2.2牛顿插值法

2.3埃尔米特插值法

2.4分段线性插值法

分段线性插值的意义在于克服拉格朗日插值法的非收敛性。其实分段线性插值就是利用每两个相邻的插值基点做线性插值，就可以得到分段线性插值函数：

2.5三次样条插值法

分段低次插值函数，虽然有收敛性，但平整度差。因此，早期的制图工程师在制图时首先会在样点处固定弹性木条，其他各处任意成形，这样就能画出一条曲线，定义样条曲线。事实上，该曲线是由分段三次曲线并接而成，在连接点也就是样点上必须要二阶连续可导，从数学角度加以归纳得到数学样条这个概念。利用样条插值方法得到的插值曲线光滑性好，但却不收敛。由此我们可以引用三次样条函数以达到插值函数的收敛性且光滑度也更好了。

三、结语

对于代码或算法的演示将会在下节展示。