2024，这将是量子计算的真正挑战

2023年，一项项量子计算纪录被打破。

谷歌量子AI团队证明了将多个量子比特分组合成为一个逻辑量子比特的纠错方法可以提供更低的容错率。以往的纠错研究随着比特数的增加，错误率会提高，都是“越纠越错”，而这次谷歌首次实现了“越纠越对”。也就是说，突破了量子纠错的盈亏平衡点。这是量子计算“万里长征”中的重要转折点，为实现通用计算所需的逻辑错误率的指出了全新途径。

IBM推出了错误率更低的Heron芯片，明年，将有更多的IBM Heron处理器加入IBM行业领先的公用事业级系统。

美国国防高级研究计划局 (DARPA)、哈佛大学、QuEra团队组成的研究小组制造出了一台量子计算机，它拥有有史以来数量最多的逻辑量子比特、最多可运行280个物理量子比特。有了这次团队的方法，科学家就不需要几千、几十万、几百万个物理量子比特来纠错了——建造实用量子计算机的竞赛可能正在进入一个新阶段。

现在，全球量子公司正将目标设定在一件尽管不那么耀眼，但却远为重要的事情上。

量子计算机具有变革的潜力，但前提是我们能够处理这些在宇宙物理极限下运行的高噪声、高灵敏度系统所固有的错误。错误处理并不是一项简单的任务；我们需要在系统设计的每一步都预测并修复这些错误。

不管是计算你该交多少税，还是玩超级马里奥，我们的计算机总是在长长的0、1比特串上施展魔法。而量子计算却是在量子比特上展示魔力。量子比特可以同时处于0和1，就像你同时坐在长沙发的两头那样。它们可以在离子、光子或者微小的超导电路中实现，这种两能级系统赋予了量子计算超强的能力。

经典比特和量子比特

不过，量子比特同时也是很脆弱的，与周围环境发生哪怕极微弱的相互作用也会导致它们发生改变。所以，科学家们必须学会如何去纠正这些错误。

在计算机中出现错误是很自然的事情：量子态应该按照所执行的量子电路的规定演化。然而，由于外部环境或硬件本身存在各种不可避免的干扰（即我们所说的噪音），实际量子态和量子比特的演化可能会有所不同，从而导致计算出错。但量子比特误差比经典比特误差更为复杂。不仅量子比特的零值或一值会发生变化，而且量子比特还带有相位：这有点像它们指向的方向。

我们需要在系统的各个层面找到处理这两种错误的方法：

- 一是改进我们对计算硬件本身的控制；

- 二是在硬件中建立冗余，这样即使有一个或几个量子比特出错，我们仍然可以检索到准确的计算值。

现在，量子计算的早期领头羊——Google、Rigetti和IBM，都已经将视角转到了这一目标上。Google量子人工智能实验室的负责人Hartmut Neven说道：“这（量子纠错）非常确定是下一个重要的里程碑”。而IBM量子计算事业的领导人Jay Gambetta则说：“接下来几年内，你们会看到我们在解决量子纠错问题上的一系列成果。”

物理学家们已经开始在小规模实验他们的量子纠错方案了，但是面临的挑战仍极艰巨。

量子计算机的追寻之路启于1994年。当时麻省理工学院的一位数学家Peter Shor展示了一种尚处于假想中的机器，它可以快速地对一个大数进行因式分解。得益于量子比特的两能级系统，Shor算法用量子波函数来表示一个大数可能的分解方式。

这些量子波可以同时在量子计算机所有的量子比特中波动，它们相互干涉，导致错误的分解形式相互抵消，最终正确的形式鹤立鸡群。现在保护着互联网通信的密码系统正是建立在一个基本事实之上，即搜索大数分解形式是常规计算机几乎不可完成的，因此运行Shor算法的量子计算机可以破解这一密码系统。当然，这只是量子计算机能做的很多事情之一。

但是，Shor假设每个量子比特都能够完好地保持其状态，这样量子波只要有必要就可以左右荡漾。真实的量子比特则远没有这么稳定。Google、IBM和Rigetti采用的量子比特都由超导金属刻蚀而成的微纳谐振电路构成。目前已经证明，这种比特比其他类型的量子比特更易于操控和电路集成。每个电路有两个确定的能态，我们可以分别记为0和1。通过在这个电路上施加微波，研究者就能使它处于其中一个状态，或者两个状态的任意组合——比如说30%的0和70%的1。

但是，这些“中间态”会在极短的时间内弥散，或者说“退相干”。甚至在退相干发生之前，噪声就可能会“冲撞”并改变这些量子态，让计算结果“出轨”，朝不想要的方向演化。

因此，有必要在当今的硬件上研究和实现代码，这不仅是为了扩大我们对如何设计更好的量子计算机的知识，也是为了帮助对当前硬件的状态进行基准测试。这有助于加深我们对系统级要求的理解，并提高我们系统的能力。

科学家们将一个量子比特——一个“逻辑量子比特”的信息分散到很多物理比特中去的方法，可以追溯到上世纪五十年代开发早期经典计算机的时代。早期计算机中的比特由真空管或者机械继电器（开关）组成，他们有时候会毫无征兆地发生反转。为了克服这个问题，著名数学家冯·诺伊曼开了纠错之先河。

冯·诺伊曼的方法利用了冗余。假设一个计算机对每个比特做了三份拷贝，那么即便其中一个翻转了，多数比特仍然保持着正确值。计算机可以通过对这几个比特做两两比对来找到并修正错误比特，这种方法被称为奇偶校验。比如说，如果第一个和第三个比特相同，但第一个和第二个、第二个和第三个都不同，那么最有可能第二个比特翻转了，于是计算机就把它再翻回来。更大的冗余意味着更大的纠错能力。

有意思的是，刻在微芯片上的晶体管，也就是现代计算机用来编码其比特的器件竟是如此的可靠，以至于纠错还真用得不多。

但是量子计算机不得不依赖于此，至少对超导量子比特构成的量子计算机而言如此。（由单个离子构成的量子比特受噪声影响更小，但更难集成）量子力学原理本身又让这一工作变得更为艰难，因为它剥夺了最简单的纠错工具——复制。在量子力学中，不可克隆定理告诉我们，不可能在不改变量子比特原始状态的情况下将其状态复制到其他量子比特上。谢菲尔德大学的一位理论物理学家Joschka Roffe说：“这就意味着我们不可能直接将经典的纠错码转换成量子纠错码。”

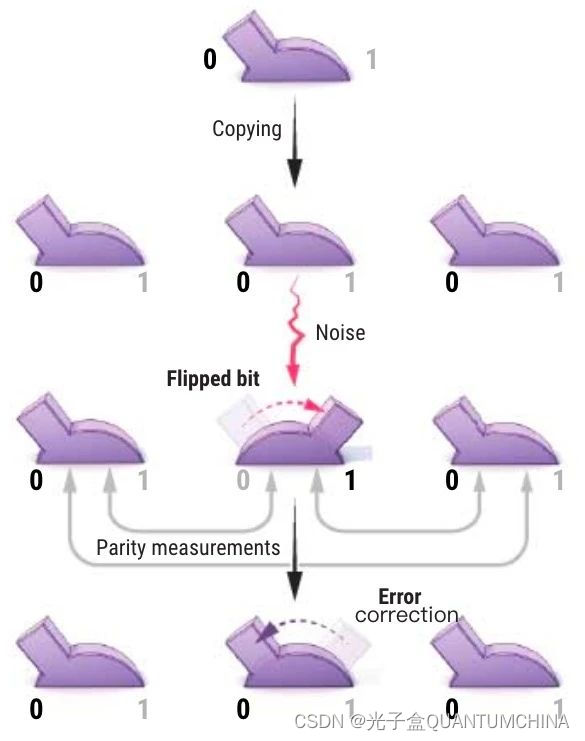
在传统计算机中，一个比特就是一个可以被设置为0或1的开关。为了保护一个比特，计算机可以将它复制到其他比特上。如果噪声引起某个拷贝发生了翻转，通过做奇偶校验，计算机就能定位到错误：将一对比特进行对比，看它们状态相同还是不同

更糟糕的是，量子力学还要求研究者蒙眼找错误。尽管量子比特可以处在0和1的叠加态上，但根据量子力学，实验者不可能在不引起塌缩的情况下测量这一叠加态，测量总导致量子态向0或1中的某个状态塌缩：测量一个态就会消灭一个态！Kuperberg说：“最简单的纠错方法（经典纠错）就是把所有比特检查一遍，看看哪里出错了。但如果是量子比特，你就必须在不看它的情况下找出错误来。”

这些障碍可能听起来难以逾越，但量子力学又指出了可能的解决方案。研究者虽然不能复制一个量子比特的态，但他们可以将其扩展到其他比特上去，利用一种难以理解的量子关联——量子纠缠。

如何实现纠缠，正显示了量子计算有多微妙。在微波的激励下，一个初始量子比特与另一个处于0态的比特通过一个“控制非”（CNOT）门操作发生相互作用。当第一个量子比特处在1态时，CNOT门改变第二个比特的状态，而当第一个比特处于0态时，则保持第二个比特不变。尽管有相互作用，但这个过程并没有对第二个量子比特做测量，因此不会迫使它的量子态塌缩。

相反，这个过程保持了第一个量子比特的双向态，并同时处在改变和不改变第二个量子比特的状态，总之，它让两个量子比特处在了同时为0和同时为1的叠加态。

举例来说，如果初始的量子比特处于30%的0和70%的1的叠加态，我们可以将它与其他比特连成一个链，比如三个量子比特共享一个纠缠态，其中30%为全0，70%为全1。这个态与初始比特的三个拷贝构成的态是不同的。实际上，这三个纠缠的量子比特串中的任何一个比特独自来看都没有一个确切的态，但它们完全关联起来了：如果你测量第一个比特而它塌缩到了1，那么另外两个比特一定也同时塌缩到了1；反之亦然，如果第一个塌缩到了0，其他两个也同时塌缩到了0。这种关联是纠缠的本质所在。

在这样一个更大的纠缠态中，科学家们现在就可以留心错误的发生了。为了做到这点，他们继续将更多的“辅助”量子比特与这个三比特链纠缠起来，一个与第一、第二比特纠缠，另一个则与第二和第三比特纠缠。之后再对辅助量子比特进行测量，就像经典比特中的奇偶校验那样。比如说，噪声可能将原先的三个编码比特中的一个翻转了，于是它的0和1部分调换了，改变了它们之间潜在的关联性。如果研究者把事情做好，他们可以在辅助量子比特上做“稳定器”测量以探测这些关联。

尽管测量辅助量子比特导致了它们状态的塌缩，但并没有对编码比特造成影响。“这是经过特别设计的奇偶校验测量，它不会导致编码在逻辑态中的信息塌缩”，Roffe说。举例来说，假如第一个辅助比特的测量结果为0，它只说明了第一和第二编码比特的状态一定相同，但并没告诉我们它们到底处在哪个态，而如果辅助比特测量结果为1，则表明编码比特肯定处于相反的态，仅此而已。如果能在量子比特态趋于弥散之前迅速找到发生翻转的比特，那就可以用微波将它再翻回原来的态并恢复其相干性。

量子力学原理使得直接通过复制并测量量子比特（上）并检测错误不可行。物理学家想到的替代办法是将量子比特的态通过纠缠（中）分散到其他量子比特中去，然后监测这些量子比特来探测错误，发现错误后再通过操控让错误比特回到正确的态（下）

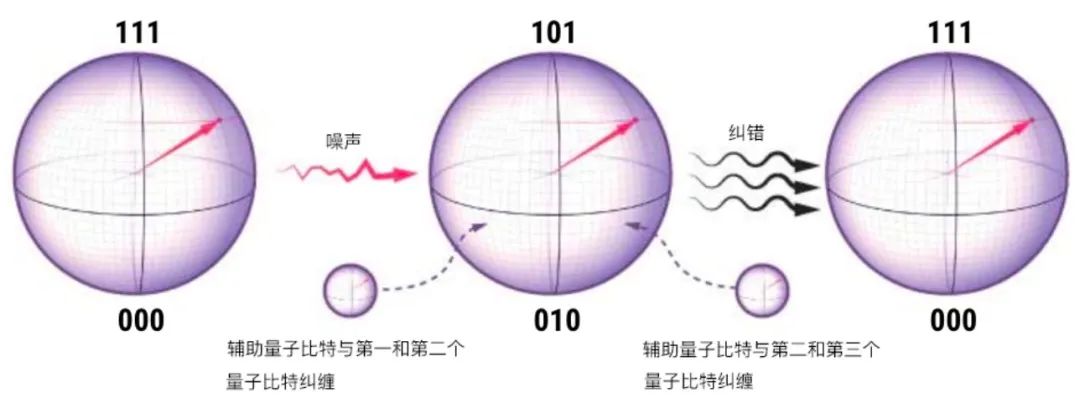
如果噪声导致一个量子比特发生了翻转，物理学家可以探测这一变化而不真正测量这个态。他们将一对主量子比特与其他辅助量子比特纠缠起来并测量这些辅助比特，如果主量子比特之间的关联保持不变，结果就应为0，而如果发生了翻转，测量结果就应为1。接下来就可以通过微波将量子比特再翻回去以恢复最初的纠缠态

这只是最基本的概念。一个量子比特态要比只是0和1的组合更为复杂。它同时还取决于这两部分是如何交织的，换句话说，它还依赖于一个抽象的角度，也就是相位。这个相位角度可以从0°到360°之间变化，它是波动干涉效应的关键，而正是这种量子干涉赋予了量子计算机超强的能力。原理上，任何量子比特态的错误可以被认为是比特翻转和相位翻转的某种组合，比特翻转对应0和1发生交换，而相位翻转对应于相位变化180度。

要修正这两种错误，研究人员可以将上述的纠错方案扩展到另一个维度。既然一个三纠缠的比特串，加上两个辅助比特交织其间，是探测和纠正一个比特翻转错误的最小结构，那么一个3x3的量子比特网格，加上8个分布其中的辅助比特，就是可以同时探测和修正比特翻转和相位翻转错误的最小结构。现在逻辑比特就存在于这样一个9比特的纠缠态中——谢天谢地你不用写出它的数学公式来！在这样一个网格上的其中一个维度上进行稳定器测量可以检测比特翻转错误，而在另一个维度上进行略微变化的稳定器测量则检测相位翻转错误。

将量子比特态放到一个二维网格中进行纠错的方案会随着量子比特的几何排布及稳定器测量的细节而改变，但研究人员进行量子纠错的路线已经清晰了：将单个逻辑量子比特编码到一个物理比特组成的网格阵列中，并展示逻辑比特的保真度随着阵列的尺度增加而增加。

通过将这些功能推向物理极限，并使用精心设计的基准对其进行评估，研究界发现了一些重要的约束条件，这些约束条件告诉我们如何在量子计算中共同设计最佳的错误抑制、缓解和纠正协议。目前，大量的QEC研究进入实验演示阶段，使用最合适的QEC代码在当今的量子硬件上实现逻辑运算。

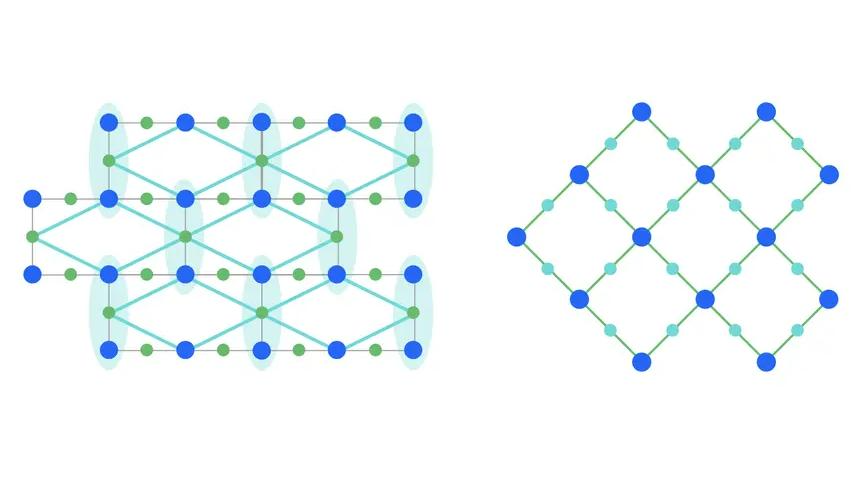
编码到3比特重复码（左）导致逻辑重方格（右）

这些演示中有许多涉及到研究人员实施表面码和相关的重六边形码方案。这些代码系列被设计用于二维的量子比特网格上，通常具有不同作用的物理量子比特：用于存储数据的数据量子比特和用于测量检查或标志的辅助量子比特。IBM通过“距离”来衡量这些代码对错误的稳健性，“距离”这个指标代表了返回一个错误的逻辑量子比特值所需的最小物理量子比特错误数。

因此，增加距离意味着更稳健的代码。逻辑量子比特误差的概率随着距离的增加呈指数级下降。

迄今为止，二维表面码在纠错方面一直被认为是无可争议的领先者；然而它有两个重要的缺陷。首先，大部分物理量子比特都用于纠错。随着表面码的距离增长，物理量子比特的数量必须像距离的平方一样增长，以编码一个量子比特。例如，一个距离为10的表面编码将需要大约200个物理量子比特来编码一个逻辑量子比特。第二，要实现一套计算上通用的逻辑门是很困难的。领先“魔法态提取”方法需要额外的资源，而不是简单地将量子信息编码为纠错码。这些额外资源的时空成本对于中小规模的计算来说可能过于昂贵。

解决表面码的第一个缺点的一个方法是，从qLDPC码的“好（good）”系列中寻找和研究代码。“好（good）”是一个技术术语，一个好的码族是指逻辑量子比特的数量和距离与物理量子比特的数量成正比；因此，物理量子比特增加一倍，逻辑量子比特的数量和距离都会增加一倍。表面码族并不“好”，寻找好的qLDPC码一直是量子纠错中的一个主要开放性问题。

当我们使用部署的纠错码执行量子计算时，我们会观察到重要的错误敏感事件：这些事件是潜在错误的线索，当它们发生时，解码器的任务是正确识别合适的错误纠正。经典硬件执行这种解码，必须跟上重要事件发生的高速率。此外，从量子设备传输到经典硬件的事件数据量不得超过可用带宽。因此，解码器对控制硬件和量子计算机与经典系统的接口方式施加了额外的限制；解决这一挑战在理论上和实验上都具有关键意义。

不能简单地对逻辑量子比特进行编码和解码；但是，我们还必须能够使用它们进行计算。因此，一个关键的挑战是找到简单、廉价的技术来实现一组计算上通用的逻辑门。同样，对于二维表面码及其变体，我们没有这样的技术，并且需要昂贵的魔法态提取技术。虽然多年来，魔发态提取成本已经降低，但它仍然远非理想，研究仍在继续改进蒸馏过程并发现不需要它的新方法和/或代码。

为了避免中期魔法态提取的开销，人们设想错误缓解和纠错协同工作，通过使用纠错来消除Clifford门的噪声和T型门上的错误缓解，从而提供通用门组。

总之，这些发现共同开辟了量子纠错的新方向，并导致了进一步的发展。

我们希望通过纠错来实现我们的终极目标：容错量子计算。在这种计算中，我们建立起冗余——这样即使有几个量子比特出现错误，系统仍能为我们在处理器上运行的任何尝试返回准确的答案。纠错是经典计算中的一项标准技术，通过冗余对信息进行编码，从而检查是否发生错误。

量子计算机是真实存在的，可以编程，但构建大型可靠的量子计算机仍然是一个重大挑战。要充分挖掘这些系统的潜力，可能需要量子纠错技术的重大进展。

量子纠错是相同的理念，但需要注意的是，我们必须考虑到上述新型错误。此外，我们还必须仔细测量系统，以避免我们的状态崩溃。在量子纠错中，我们将单个量子比特值（称为逻辑量子比特）在多个物理量子比特之间进行编码，并实施门，将物理量子比特结构视为本质上无差错的逻辑量子比特。我们执行一组特定的操作和测量，合称为纠错码，以检测和纠正错误。根据阈值定理，我们知道在应用纠错之前，我们的硬件必须达到一个与硬件相关的最小错误率。

但纠错不仅仅是一个工程挑战，它还是一个物理和数学问题。目前领先的编码表面码，需要为每个单逻辑量子比特提供大量的物理量子比特 O(d^2)，其中 d 是编码的一个特征，称为其距离，与可纠正的错误数量有关。为使 QEC 代码能够纠正足够多的错误以实现容错，必须选择足够高的距离 d，使代码的纠错能力与量子设备的错误率相匹配。由于目前的量子设备噪声很大，误差率接近 1e-3，这意味着采用表面代码进行量子纠错所需的量子比特数量目前并不现实——每个逻辑量子比特需要太多的物理量子比特。为了向前迈进，我们既需要降低设备的物理错误率，比如说降低到 1e-4，又需要发现需要更少物理量子比特的新代码。

世界各地的理论家们仍在设计不同的纠错策略和量子比特布局，以确定哪些策略和布局对未来最有前景，幸运的是，我们似乎正在进入另一个创造性的时期，因为该领域开始向新的方向推进，最近的进展，如新的qLDPC代码，显示了未来系统的前景。

参考链接：

[1]https://research.ibm.com/blog/future-quantum-error-correction

[2]https://arxiv.org/abs/2207.06428[17]https://arxiv.org/abs/2203.07205[18]https://www.science.org/doi/10.1126/sciadv.aay4929

[3]https://medium.com/qiskit/why-this-quantum-pioneer-thinks-we-need-more-people-working-on-quantum-algorithms-3020729c61e1