线性方程组的数值解法-3

共轭梯度法

1.Ritz变分问题

2.最速下降法

原理，首先获取负梯度方向，沿着负梯度方向前进α步

3.一维极小搜索

指的是给定前进方向p，对上述α进行求导，搜索最低点的方式。这里没有指定p是r。

4.最速下降法的性质

相邻两次搜索方向是正交的，即(rk+1,rk) = 0

下一次的搜索方向等于：

误差估计：

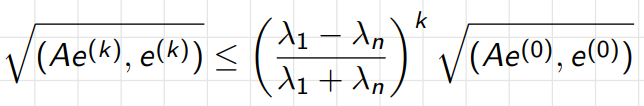
4.共轭梯度法

共轭的含义：在A内积下正交

性质：两两A共轭的一组向量，线性无关?

进而，x可以转换为一组A共轭的向量组的加权求和，系数可以由内积求出。问题转化为找到这组A共轭向量组

如何构造A共轭向量组？施密特正交化（新的向量通过减去在前面向量的A投影得到）

与最速下降法的区别在于，除第一步外，不再以残差（负梯度）作为前进方向，而是以A共轭的方向前进，以下是完整步骤

更简单的形式

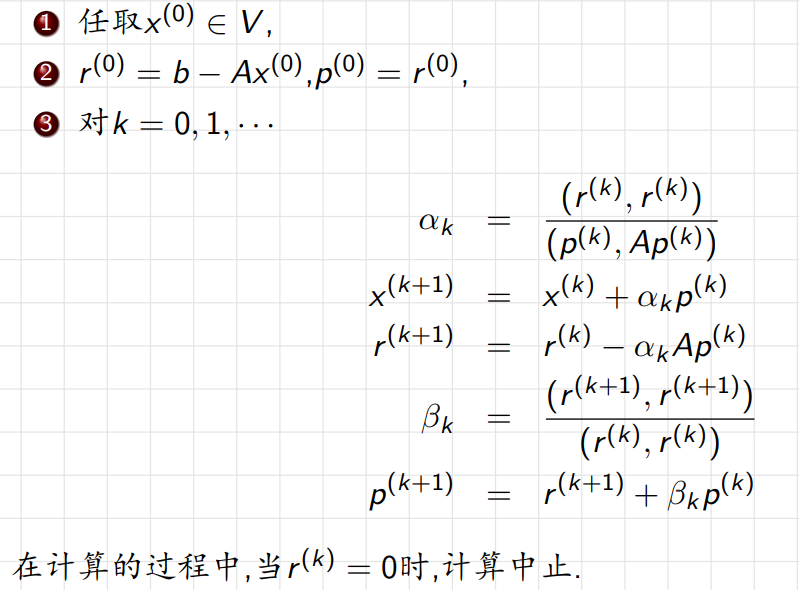
误差估计

关于误差：不超过n步一定能够得到精确解

截图源自

【《数值分析》| 华科 | 研究生基础课】https://www.bilibili.com/video/BV1AK4y1k7Px?p=34&vd_source=a53b34e44cbfd40d72a5b337c3e5a13d

【数值分析6(3共轭梯度法)苏州大学】https://www.bilibili.com/video/BV16a4y1t76z?vd_source=a53b34e44cbfd40d72a5b337c3e5a13d