【递归、搜索与回溯】综合练习
发布时间:2024年01月01日

欢迎来到Cefler的博客😁
🕌博客主页:那个传说中的man的主页
🏠个人专栏:题目解析
🌎推荐文章:题目大解析(3)

👉🏻找出所有子集的异或总和再求和
原题链接:找出所有子集的异或总和再求和
mycode:
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void dfs(vector<int>& nums,int n)
{
for(int i = n ;i<nums.size();i++)
{
path.push_back(nums[i]);
dfs(nums,i+1);
path.pop_back();
}
res.push_back(path);
}
int subsetXORSum(vector<int>& nums) {
dfs(nums,0);
int Sum = 0;
for(int i = 0;i<res.size();i++)
{
int sum = 0;
for(auto e:res[i])
{
sum^=e;
}
Sum+=sum;
}
return Sum;
}
};
优化代码(纯递归):
class Solution {
public:
int Sum = 0,sum = 0;
void dfs(vector<int>& nums,int n)
{
for(int i = n ;i<nums.size();i++)
{
sum^=nums[i];
dfs(nums,i+1);
sum^=nums[i];//再异或一遍可以消掉
}
Sum+=sum;
}
int subsetXORSum(vector<int>& nums) {
dfs(nums,0);
return Sum;
}
};
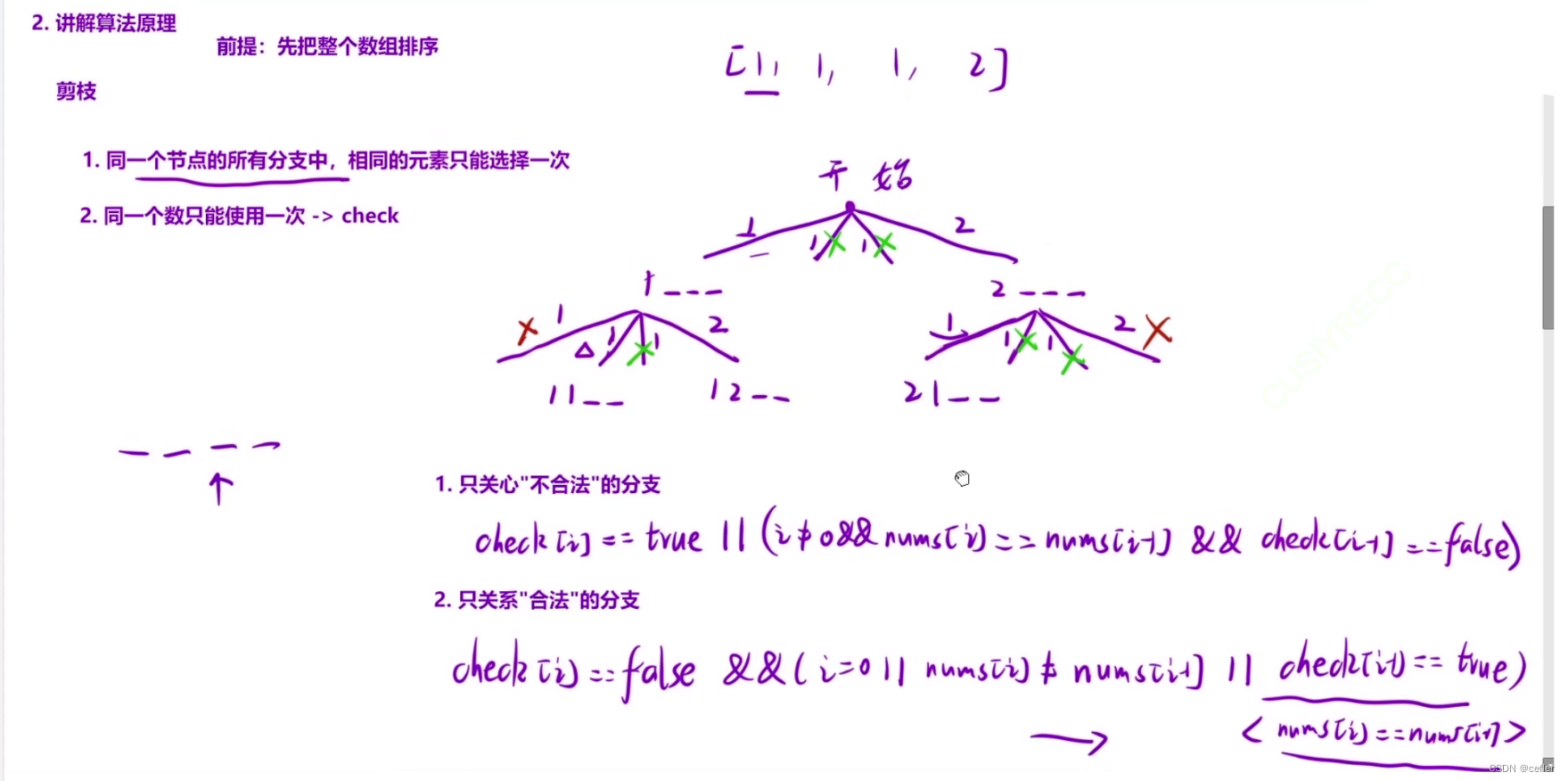
👉🏻全排列 II
原题链接:全排列 II
mycode:
class Solution {
public:
vector<vector<int>> ret;
vector<int> path;
bool check[8];//检查该位置是否被用过了,true说明被用过了
void dfs(vector<int>& nums)
{
if(nums.size()==path.size())//说明此时已经组成一个序列了
{
ret.push_back(path);
return;
}
for(int i = 0;i<nums.size();i++)
{
if(check[i]==false && (i==0||nums[i]!=nums[i-1]||check[i-1]==true))//此时还没被用过&&第一层||前后值不重复相等||不在同一层
{
path.push_back(nums[i]);
check[i] = true;
dfs(nums);
//回溯清空现场,将dfs下层插入的元素pop掉
path.pop_back();
check[i] = false;
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
//前提先排序
sort(nums.begin(),nums.end());
dfs(nums);
return ret;
}
};
👉🏻电话号码的字母组合
原题链接:电话号码的字母组合
mycode:
class Solution {
public:
const char* numsArr[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
void Combine(const string& digits,string combinestr,int i ,vector<string>& ret)
{
if(i == digits.size())//当数字中的字母全部都进行完组合后
{
ret.push_back(combinestr);
return;
}
int num = digits[i] - '0';
string str = numsArr[num];
for(auto ch:str)
{
Combine(digits,combinestr+ch,i+1,ret);
}
}
vector<string> letterCombinations(const string& digits) {
vector<string> v;//存储全部组合的字符串
if(digits=="")
return v;
string str;//这个是专门用来组合的字符串
int i =0;
Combine(digits,str,i,v);
return v;
}
};
加入恢复现场代码优化:
class Solution {
public:
const char* numsArr[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> ret;
string combinestr;
void Combine(const string& digits,int i )
{
if(i == digits.size())//当数字中的字母全部都进行完组合后
{
ret.push_back(combinestr);
return;
}
int num = digits[i] - '0';
string str = numsArr[num];
for(auto ch:str)
{
combinestr+=ch;
Combine(digits,i+1);
//恢复现场
combinestr.pop_back();
}
}
vector<string> letterCombinations(const string& digits) {
if(digits=="")
return ret;
Combine(digits,0);
return ret;
}
};
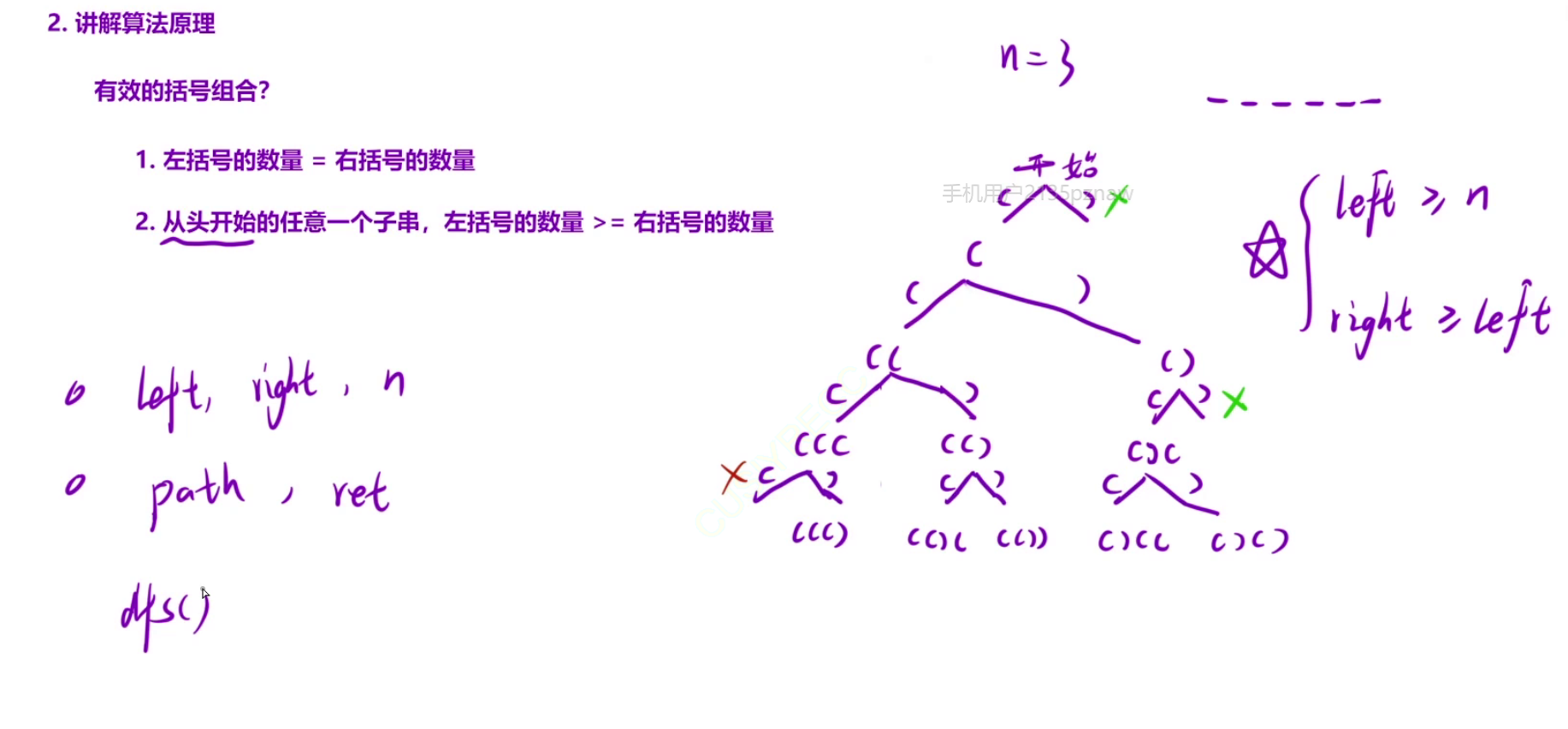
👉🏻括号生成
原题链接:括号生成
mycode:
class Solution {
public:
vector<string> ret;
string path;
int left = 0,right = 0;
void dfs(int n)
{
if(left+right==2*n)
{
ret.push_back(path);
return;
}
if(left<n)
{
path.push_back('(');
left++;
dfs(n);
path.pop_back();
left--;
}
if(right<left)
{
path.push_back(')');
right++;
dfs(n);
path.pop_back();
right--;
}
}
vector<string> generateParenthesis(int n) {
dfs(n);
return ret;
}
};
👉🏻组合
原题链接:组合
mycode:
class Solution {
public:
vector<vector<int>> ret;
vector<int> path;
int _k;
void dfs(int n,int pos)
{
if(path.size()==_k)
{
ret.push_back(path);
return;
}
for(int i = pos;i<=n;i++)
{
path.push_back(i);
dfs(n,i+1);//i+1是换层,n+1是在同一层里换元素
//恢复现场
path.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
_k = k;
dfs(n,1);
return ret;
}
};
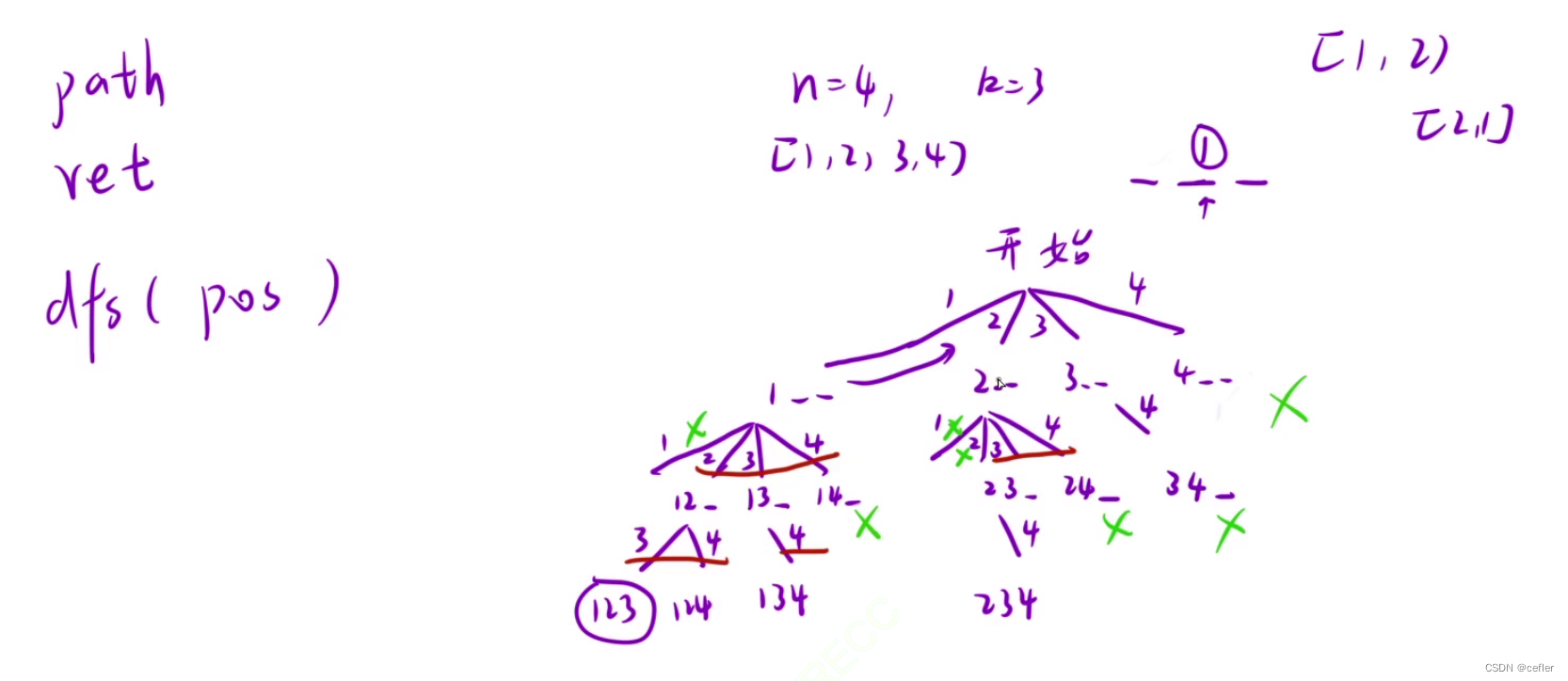
如这种左大右小的树,一般就是i+1进行深度优先遍历,如果是完全二叉树,则是n+1这种广度遍历
文章来源:https://blog.csdn.net/cefler/article/details/135323381
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!