【排序算法】C语言实现归并排序，包括递归和迭代两个版本

🚀前言

大家好啊！阿辉接着更新排序算法，今天要讲的是归并排序，这里阿辉将讲到归并排序的递归实现和迭代实现，话不多说，开始咱们今天的学习吧！！！！

🚀归并排序介绍及其思想

归并排序这是阿辉讲的第一个时间复杂度O(nlogn)的排序算法，额外空间复杂度是O(n)，归并排序可以做到稳定性。

思想
归并排序的思想就是分治，分治的思想是将一个大问题分解成若干个小问题，然后分别解决这些小问题，最后将这些小问题的解合并起来得到原问题的解

由分治的思想很容易，想到用递归来实现归并排序，我们接着看👇

🚀递归实现

关于归并排序的递归方法主要由三个大的逻辑组成：

• 分解：将待排序的数组分成两个子数组
• 解决：对每个子数组进行排序
• 合并：将排序好的子数组合并成一个有序的数组

这里我们使用递归很轻松就能把主逻辑写好，大家都知道写递归必须要有限制条件否则会造成死递归，对于归并排序的限制条件很简单，对于数组只有一个元素时自然就是有序的，直接返回即可

主逻辑：
merge函数相当于黑盒，作用就是把两个有序数组合成一个大的有序数组

void MergeSort(int a[], int l, int r) {// C/C++归并排序递归版本，主逻辑
	if (r == l) {//递归限制条件
		return;
	}
	int m = l + ((r - l) >> 1);//数组中位置下标
	MergeSort(a, l, m);//左部分排序
	MergeSort(a, m + 1, r);//右部分排序
	merge(a, l, m, r);//两部分有序数组合并
}

整个归并排序最重要的部分也就是有序数组合并的部分：

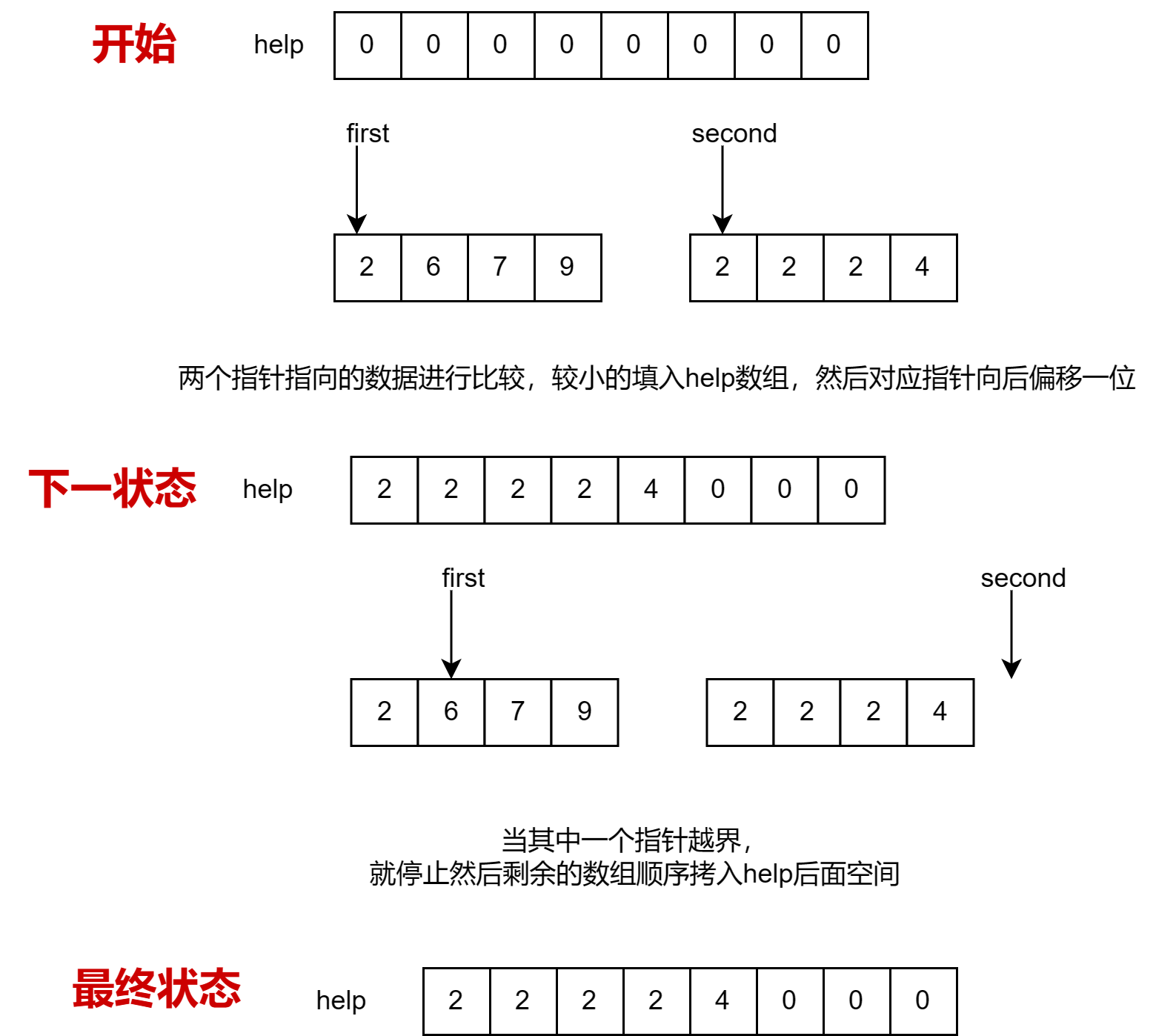
merge函数实现，还是不太懂的可以看一下下面的代码，有详细的注释
C语言版本：

void merge(int a[], int l, int m, int r) {
	int* help = (int*)malloc((r - l + 1) * 4);//申请辅助空间
	int i = 0;//作为help指针的偏移量，存储两有序数组排好序的大数组
	int first = l;//作为左部分数组的起始下标
	int second = m + 1;//作为右部分数组的起始下标
	while (first <= m && second <= r) {//哪一方下标越界就说明不用继续比较了
		//三目运算代码更简洁，谁小谁在前先赋值给help，后置++，
		// 赋值后i向后偏移一个位置，second或first也向后偏移一个位置
		help[i++] = a[first] <= a[second] ? a[first++] : a[second++];
	}
	//下面虽然两个while循环但是只会进去一个
	//还没存进help数组的继续存
	while (first <= m) {
		help[i++] = a[first++];
	}
	while (second <= r) {
		help[i++] = a[second++];
	}
	//最后把help管理的值，还原到原数组a中
	for (i = 0; i < r - l + 1; i++) {
		a[l + i] = help[i];
	}
	free(help);//释放申请的堆空间
	help = NULL;//野指针系上绳子
}

C++版本：
也就是用了STL的容器更方便

 void merge(vector<int>& arr, int l, int mid, int r) {//合并有序数组
	vector<int> help(r - l + 1, 0);//用一个额外的数组装排好的数
	int first = l;
	int second = mid + 1;
	int i = 0;
	//合并过程
	while (first <= mid && second <= r) {
		help[i++] = arr[first] <= arr[second] ? arr[first++] : arr[second++];
	}
	while (first <= mid) {
		help[i++] = arr[first++];
	}
	while (second <= r) {
		help[i++] = arr[second++];
	}
	//将help数组拷贝到原数组
	for (int i = 0; i < r - l + 1; i++) {
		arr[l + i] = help[i];
	}
}

🚀迭代实现

归并排序的迭代实现就是把主逻辑从递归改为迭代了，有序合并部分并没有改变还是上面实现的merge函数
其实就是从递归的条件返回那一步往后推：
这里我们引入一个概念步长，用来表示左部分和右部分的数组长度，步长从1开始，然后每次倍增，就相当于递归的回溯过程
上图：
步长为左右部分长度，左右部分进行merge操作，没有右部分的跳过

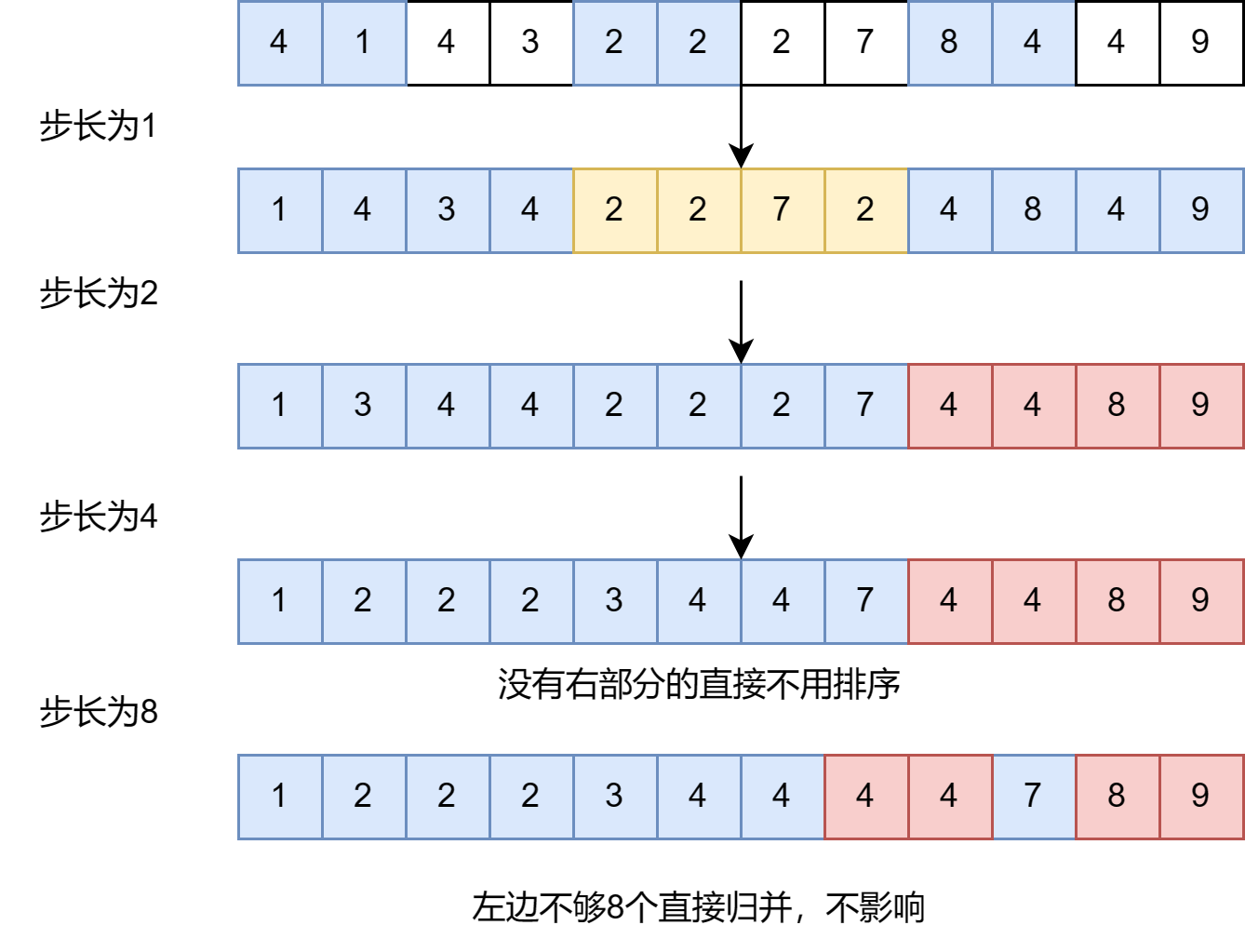
主逻辑：

void MergeSort(int a[], int l, int r) {
	int len = 1;//步长
	while (len <= r) {
		l = 0;
		while (l <= r) {
			int m = l + len - 1;//计算左部分的最后一个位置
			if (m >= r) {//此时说明没有右部分，可以跳出循环进行下一轮了
				break;
			}
			//m + len是右部分的最后一个位置与r做比较防止越界，拿到一个正确的merge右边界
			int n = r <= m + len ? r : m + len;
			merge(a, l, m, n);
			l = n + 1;
		}
		if (len > r / 2) {//假如数组很长len×2可能溢出，防止溢出变成负数死循环
			break;
		}
	}
}

merge函数和前面的一样，阿辉就不水了

---