数字逻辑电路_高教出版社
contents
前言
博客起源:本博客记录了个人学习数字逻辑电路期间做的一些笔记,其中含有PPT的截图或者个人的一些见解与思考,多有不足还望包含与指出,祝各位学习愉快
参考教材:《工程数学 线性代数》同济第七版
笔记范围:一至六章,其中第三章只关注第2目,第六章只关注同步时序逻辑电路的分析以及计数器
一、数字逻辑概论
1.1 数字信号与数字电路
1.1.1 数字技术的发展及其应用
-
电流控制器件
- 电子管
- 晶体管(二极管、三极管)
- 半导体集成电路
-
EDA(Electronic Design Automation)技术:硬件设计软件化
- 设计:EWB or Verilog
- 仿真
- 下载
- 验证结果
1.1.2 数字集成电路的分类及特点
-
数字集成电路的分类
-
从结构特点及其对输入信号的响应规则角度
- 组合逻辑电路
- 时序逻辑电路
-
从电路的形式角度
- 集成电路
- 分立电路
-
从器件的角度
- TTL电路
- CMOS电路
-
从集成度的角度
集成度:每一个芯片所包含的门个数
- 小规模
- 中规模
- 大规模
- 超大规模
- 甚大规模
-
-
数字集成电路的特点
- 稳定性高:抗干扰能力强
- 易于设计:对0和1表示的信号进行逻辑运算和处理
- 便于集成:体积小、通用性好、成本低
- 可编程性:可实现硬件设计软件化
- 高速度、低功耗
- 便于存储、传输、处理
-
数字电路的分析、设计与测试
- 分析方法
- 目标:确定输入与输出
- 工具:逻辑代数
- 方法:真值表、功能表、逻辑表达式和波形图
- 设计方法
- 从功能要求出发,选择合适的逻辑器件进行设计
- 设计方式:传统的设计方法 or 基于EDA的软件设计方法
- 测试技术
- 分析方法
1.1.3 模拟信号与数字信号
-
模拟信号:时间和数值均连续变化的信号
-
数字信号:时间和数值均离散变化的信号
-
模拟量的数字表示:模数转换,即将连续的模拟信号经过采样与编码转化为数字信号
- 首先对时间离散
- 然后对幅值离散
- 最后对得到的数字量进行编码
1.1.4 数字信号的描述方法
-
二值数字逻辑和逻辑电平
二值数字逻辑:0和1两种状态(定量)
逻辑电平:高电压和低电压(定性)
表1 正逻辑关系表(负逻辑相反) 电压(V) 二值逻辑 电平 3.5~5 1 H(高电压) 0~1.5 0 L(低电压) -
数字波形
-
实际数字信号波形
-
波形图、时序图或定时图
1.2 数制
( N ) r = ∑ i = ? ∞ ∞ K i ? r i (N)_r=\sum_{i=-\infty}^\infty K_i\ r^i (N)r?=i=?∞∑∞?Ki??ri
1.2.1 十进制
1.2.2 二进制
优点:易于表达;二进制数字电路逻辑简单,所用元件少;基本运算规则简单,运算操作方便
波形表示:应用比如“计数器”
数据传输:应用比如“串行传输”
1.2.3 十-二进制之间的转换
十进制小数转化为二进制:将小数部位不断×2,取整数,直到没有小数部分为止
1.2.4 十六进制和八进制
二进制转十六进制:从右往左每四位换算成十六进制
二进制转八进制:从右往左每三位换算成八进制
1.3 二进制数的算术运算
1.3.1 无符号二进制数的运算
1.3.2 有符号二进制数的运算
定义:其实就是多了一个符号位,且不可以省略。其中0表示正数,1表示负数:
(
+
11
)
D
=
(
01011
)
B
(
?
11
)
D
=
(
11011
)
B
(+11)_D=(01011)_B \\ (-11)_D=(11011)_B \\
(+11)D?=(01011)B?(?11)D?=(11011)B?
补码、反码和原码:
-
对于正数,补码反码原码全部一样
-
对于负数,反码为:符号位不动,原码按位取反;补码为:反码最低位+1即可
加法:与十进制竖式计算类似
减法:与十进制竖式计算类似
溢出:是因为数值位不够了,解决方法是进行位扩展
溢出的判别:
-
两个正数的求和,得到的补码的最高位如果为 1,则溢出
-
两个负数的求和,得到的补码的最高位如果为 0,则溢出
1.4 二进制代码
1.4.1 二-十进制码
其实就是在表示 0-15 的十六个二进制里面,按照不同的规则选取 10 个二进制数来进行转换
- 有权码 - 最接近逻辑的:8421BCD码
- 无权码
1.4.2 格雷码
1.4.3 ASCII码
1.5 二值逻辑变量与基本逻辑运算
1.5.1 常见逻辑符号示例
| 运算类型 | 逻辑符号 | 逻辑表达式 |
|---|---|---|
| 与 | 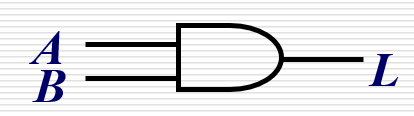 | Y = A B Y=AB Y=AB |
| 或 | 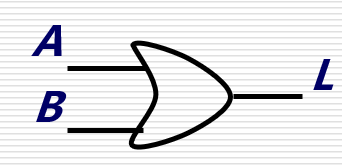 | Y = A + B Y=A+B Y=A+B |
| 非 | 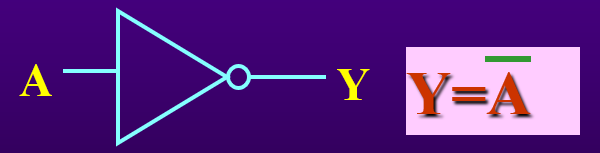 | Y = A  ̄ Y=\overline{A} Y=A |
| 与非 |  | Y = A B  ̄ Y=\overline{AB} Y=AB |
| 或非 | 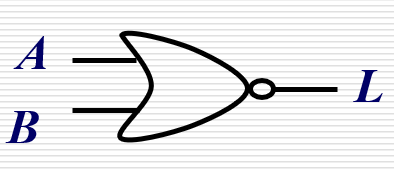 | Y = A + B  ̄ Y=\overline{A+B} Y=A+B? |
| 异或 | 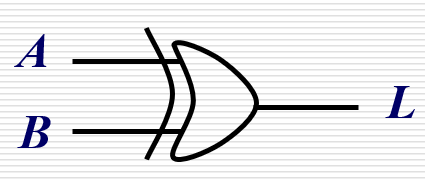 | Y = A  ̄ B + A B  ̄ = A ⊕ B Y=\overline A B+A \overline B=A \oplus B Y=AB+AB=A⊕B |
| 同或 | 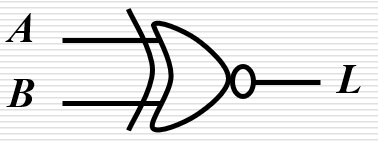 | Y = A B + A ˉ B ˉ = A ⊙ B Y = AB + \bar A \bar B = A\odot B Y=AB+AˉBˉ=A⊙B |
| 与或非 | 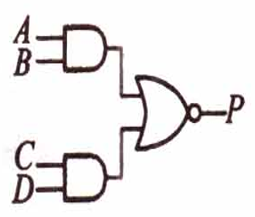 | Y = A B + C D  ̄ Y=\overline{AB+CD} Y=AB+CD? |
1.5.2 使用逻辑函数表示实际问题
| 实际问题 | 图片示例 | 变量表示 | 列真值表 | 逻辑函数 |
|---|---|---|---|---|
 |  |  |  |  |
1.6 逻辑函数及其表示方法
描述输入逻辑变量和输出逻辑变量之间的因果关系,称为逻辑函数
1.6.1 逻辑函数的几种表示方法
| 方法 | 示例 |
|---|---|
| 真值表 |  |
| 逻辑函数表达式 |  |
| 逻辑图 |  |
| 波形图 |  |
1.6.2 逻辑函数表示方法之间的转换
真值表到逻辑图的转换
-
查看真值表
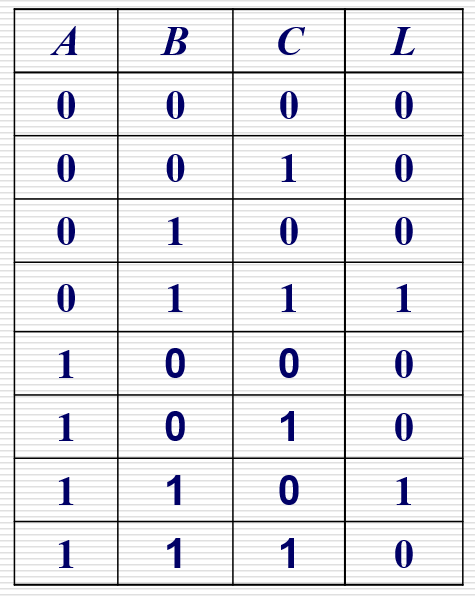
-
根据真值表写出逻辑表达式
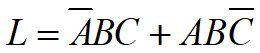
-
化简(上式不用化简)
-
绘制逻辑图
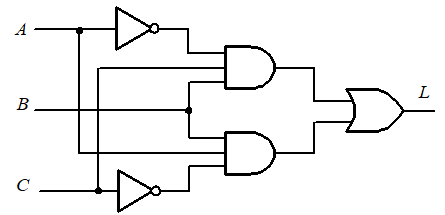
逻辑图到真值表的转换
-
根据逻辑图逐级写出表达式
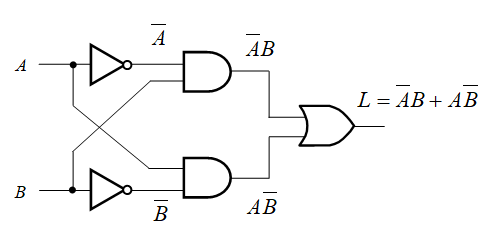
-
化简
-
代入所有输入变量求真值表

二、逻辑代数与硬件描述语言基础
2.1 逻辑代数的基本定律和规则
2.1.1 逻辑代数的基本定律和恒等式??
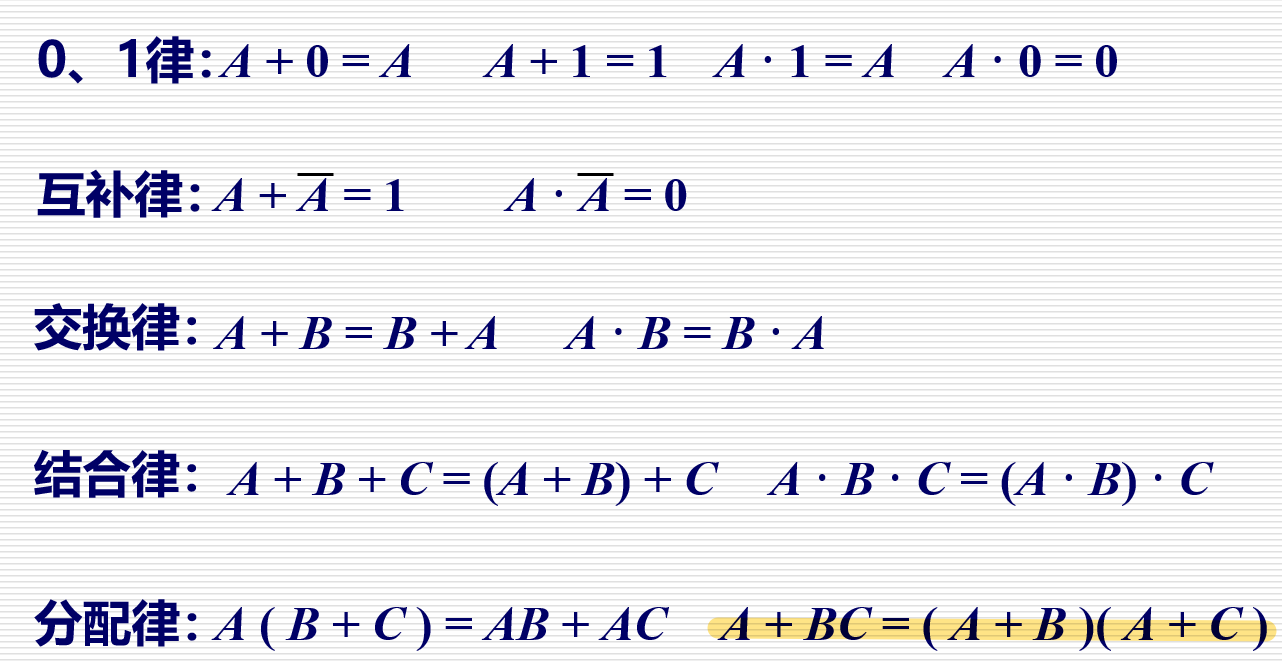

2.1.2 逻辑代数的基本规则
-
代入规则 - 类似于换元

-
反演规则(获得反函数 Y  ̄ \overline Y Y )
觉得烦可以直接进行取反运算,简单明了不会错
- 对于任意一个逻辑表达式L,与门 & 或门取反,变量取反,0 & 1取反
- 保持原来的运算优先顺序(即如果在原函数表达式中,AB之间先运算,再和其他变量进行运算,那么非函数的表达式中,仍然是AB之间先运算)
- 对于反变量以外的非号应保留不变

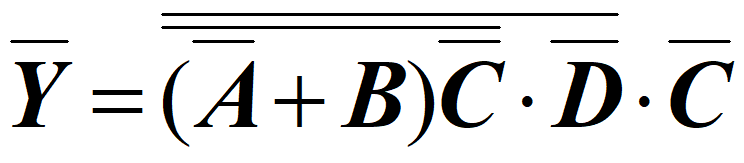
-
对偶规则(获得对偶式 L ′ L' L′ )
- 对于任何逻辑函数式:与门、或门取反,0、1 取反
2.2 逻辑函数表达式的形式
2.2.1 逻辑函数表达式的基本形式
-
与或表达式:若干个与项相或

-
或与表达式:若干个或项相与

2.2.2 最小项与最小项表达式
-
最小项的定义和性质:n 个变量的最小项一共有 2 n 2^n 2n 个
-
最小项表达式:所有的最小项相或

2.2.3 最大项与最大项表达式
-
最大项的定义和性质:n 个变量的最大项一共有 2 n 2^n 2n 个
-
最大项表达式:所有的最大项相与
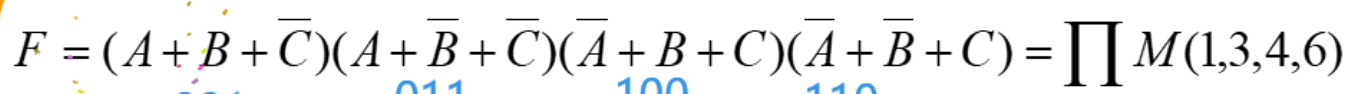
2.2.4 最大项和最小项的关系
m i = M i  ̄ m_i=\overline {M_i} mi?=Mi??
2.3 逻辑函数的代数化简法
为什么要学化简?因为化简之后可以减少门的使用,从而增强电路可靠性、降低成本
2.3.1 逻辑函数的最简形式
最简与或表达式:包含的与项数最少,且每个与项中变量数最少的与或表达式
2.3.2 逻辑函数的代数化简法
-
逻辑函数的化简
方法 逻辑函数 证明 并项法 A + A  ̄ = 1 A+\overline A = 1 A+A=1 显然 吸收法 A + A B = A A+AB = A A+AB=A 提取公因子 消去法 A + A  ̄ B = A + B A+\overline A B = A+B A+AB=A+B 摩根定律使用两次 配项法 A = A ( B + B  ̄ ) A = A(B + \overline B) A=A(B+B) 显然 -
逻辑函数形式的变换
使用场景:通常在一片集成电路芯片中只有一种门电路,为了减少门电路的种类,需要对逻辑函数表达式进行变换
变换方法:常常使用两次取反的套路进行变换

2.4 逻辑函数的卡诺图化简法
2.4.1 用卡诺图表示逻辑函数
首先写出逻辑函数的表达式并且转化为最小项表达式,最后将最小项填入相应的矩阵中即可
2.4.2 用卡诺图化简逻辑函数
尽可能使得圈出来的 2 k 2^k 2k 圈中包含的数尽可能的多,即让 k k k 尽可能的大。注意:圈中的数全部都得是最小项的数
2.5 硬件描述语言 V e r i l o g ? H D L Verilog\ HDL Verilog?HDL 基础
为了从软件代码的角度描述电路,从下面三个方面介绍如何用相关的方式进行描述
2.5.1 门级描述
门级元件中,第一个位置是输出变量,之后的都是输入变量,可解释为:多输入门
| 门级元件 | 元件符号 |
|---|---|
| 与 | and |
| 或 | or |
| 非 | not |
| 与非 | nand |
| 或非 | nor |
| 异或 | xor |
| 同或 | xnor |
2.5.2 数据流描述
简单的概括就是使用相关的位运算进行表述,因为电路逻辑本就是二元逻辑,因此位运算就刚好匹配。在使用数据流进行电路描述时,采用的语句都是连续赋值语句,由 assign 关键词开始,多条 assign 语句是并行运行的
需要注意的是,在连续赋值语句中,被赋值的变量一定是 wire 的线网类型的变量,示例如下
// 其中 Y 为 wire 类型的变量
assign Y = (~S & D0) | (S & D1)
2.5.3 行为描述
简单的概括就是使用底层语言进行编程,类似于最开始的 C 语言。使用行为描述语句进行描述时,使用 always 关键字开始变量赋值逻辑,多条 always 语句是串行运行的
需要注意的是,在行为描述语句中,被赋值的变量一定是 reg 等寄存器类型的变量,这与上述数据流描述的方式不同,示例如下
// 其中 Y 为 reg 类型的变量
always@(*) // * 为敏感变量,对于组合电路而言,所有的输入都是敏感变量
if (S) Y = D1;
else Y = D0;
三、逻辑门电路
3.1 逻辑门电路简介
MOS 管含有 NMOS 管和 PMOS 管,NMOS 管与 PMOS 管的组合称为互补 MOS,或称为 CMOS 电路
3.2 基本CMOS逻辑门电路
附上启蒙的博客:MOS管及简单CMOS逻辑门电路原理图解析!
| 器件 | 电路 |
|---|---|
| 开关 |  |
| 反相器(非门) |  |
| 与非门 |  |
| 或非门 | 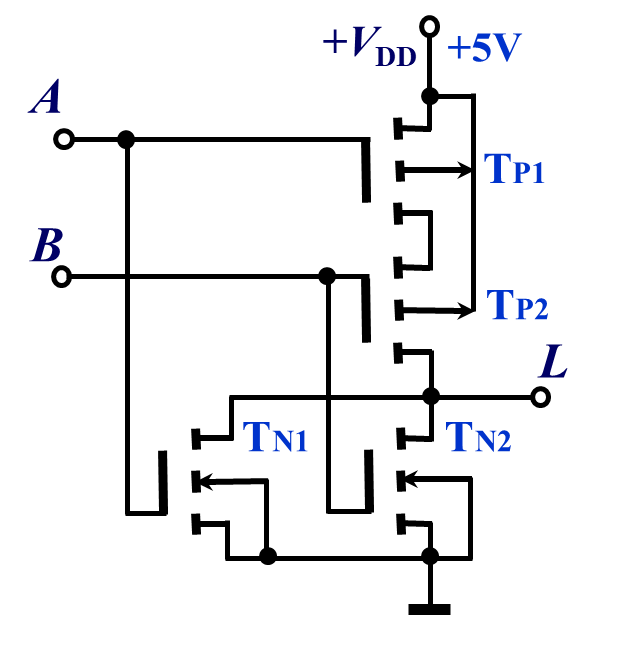 |
| 传输门(开关) | 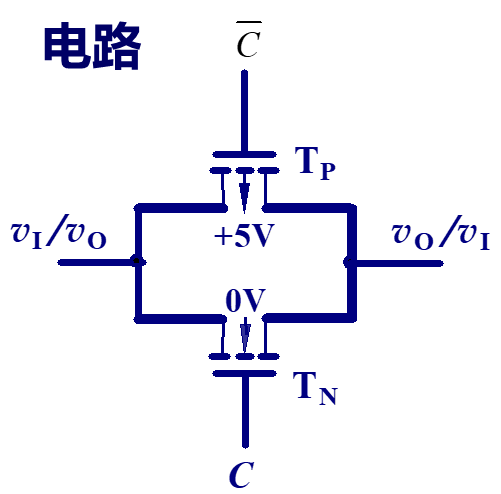 |
| 与门 |  |
| 或门 | 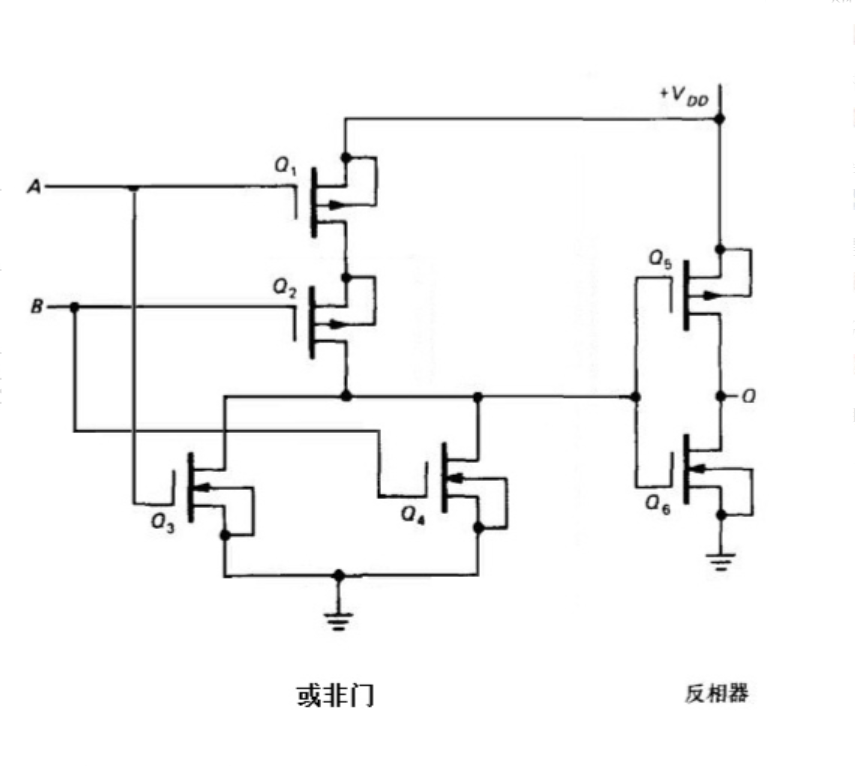 |
应用示例
解读的逻辑其实很简单,在理解之前,应该首先观看上面给出的连接中的 MOS 电路的简化版,从而理解电路的正确结构!即,每一个 MOS 管都理解为一个开关,何时闭合与断开完全取决于相应的 MOS 管的种类与电平,如果是 NMOS 管,即箭头指向左边的,为高电平导通,PMOS 管则相反,只需要知道此电路基本逻辑,那么接下来的分析结果就是水到渠成的事
需要知道一个理念就是,两个电路如果是并联的存在,那么逻辑表达式就是或,简称为并联相或;对应的,两个电路如果是串联的存在,那么逻辑表达式就是与,简称为串联相与。最后需要补充一点的就是关于取反的辨识,我们知道一个反相器 MOS 管的逻辑是非常简单的,就是一个 NMOS 管和一个 PMOS 管的组合,那么只需要在分析多个线路是串联还是并联的关系之后,最后经过一个反相器就是一个取反逻辑
| 电路 | 逻辑表达式 | 功能描述 |
|---|---|---|
 |  | 异或门 |
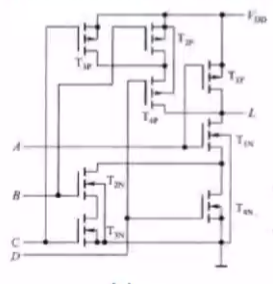 | L = ( B C + D ) A  ̄ L=\overline{(BC+D)A} L=(BC+D)A? | |
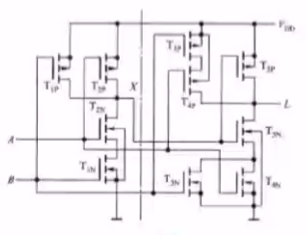 | L = ( A + B ) X  ̄ = ( A + B ) A B  ̄  ̄ = A ⊙ B L=\overline{(A+B)X}=\overline{(A+B)\overline{AB}}=A\odot B L=(A+B)X?=(A+B)AB?=A⊙B | 同或门 |
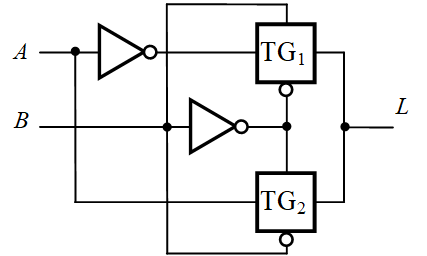 |  | 异或门 |
 |  | 2选1数据选择器 |
四、组合逻辑电路??
4.1 组合逻辑电路的分析
4.1.1 定义
只取决于实时输入,从而给出相应的输出,与之前的运行结果无关。没有反馈,没有记忆单元
4.1.2 分析步骤与方法
- 由逻辑图得到逻辑表达式
- 化简和变换
- 列真值表
- 根据真值表(或者波形图)分析电路功能
4.2 组合逻辑电路的设计
4.2.1 设计过程
- 明确逻辑含义:确定输入输出并定义逻辑状态的含义
- 列出真值表:根据逻辑描述写出真值表
- 写出逻辑表达式:由真值表写出逻辑表达式,真值取原、假值取反
- 化简逻辑表达式:代数化简法 or 卡诺图化简法
- 画出逻辑图:使用相应的门级元件进行组合连接
4.2.2 优化实现
| 电路类型 | 优化策略 | 电路图 | 优化结果 |
|---|---|---|---|
| 单输出电路 | 统一元件类型 | 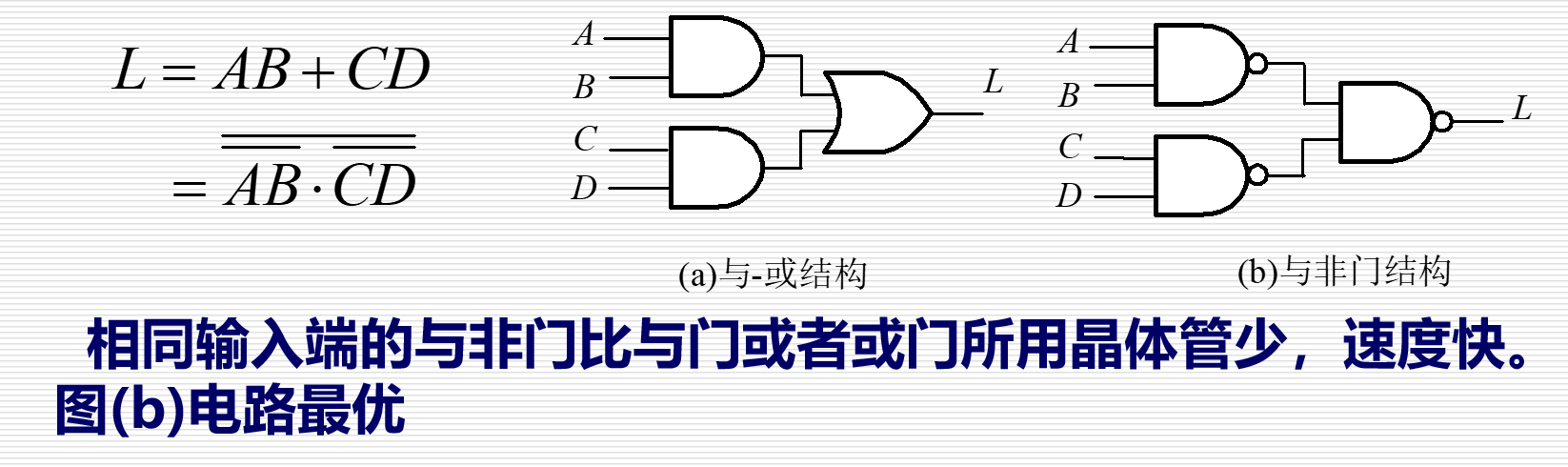 | 见左图文字 |
| 多输出电路 | 共享相同逻辑项 | 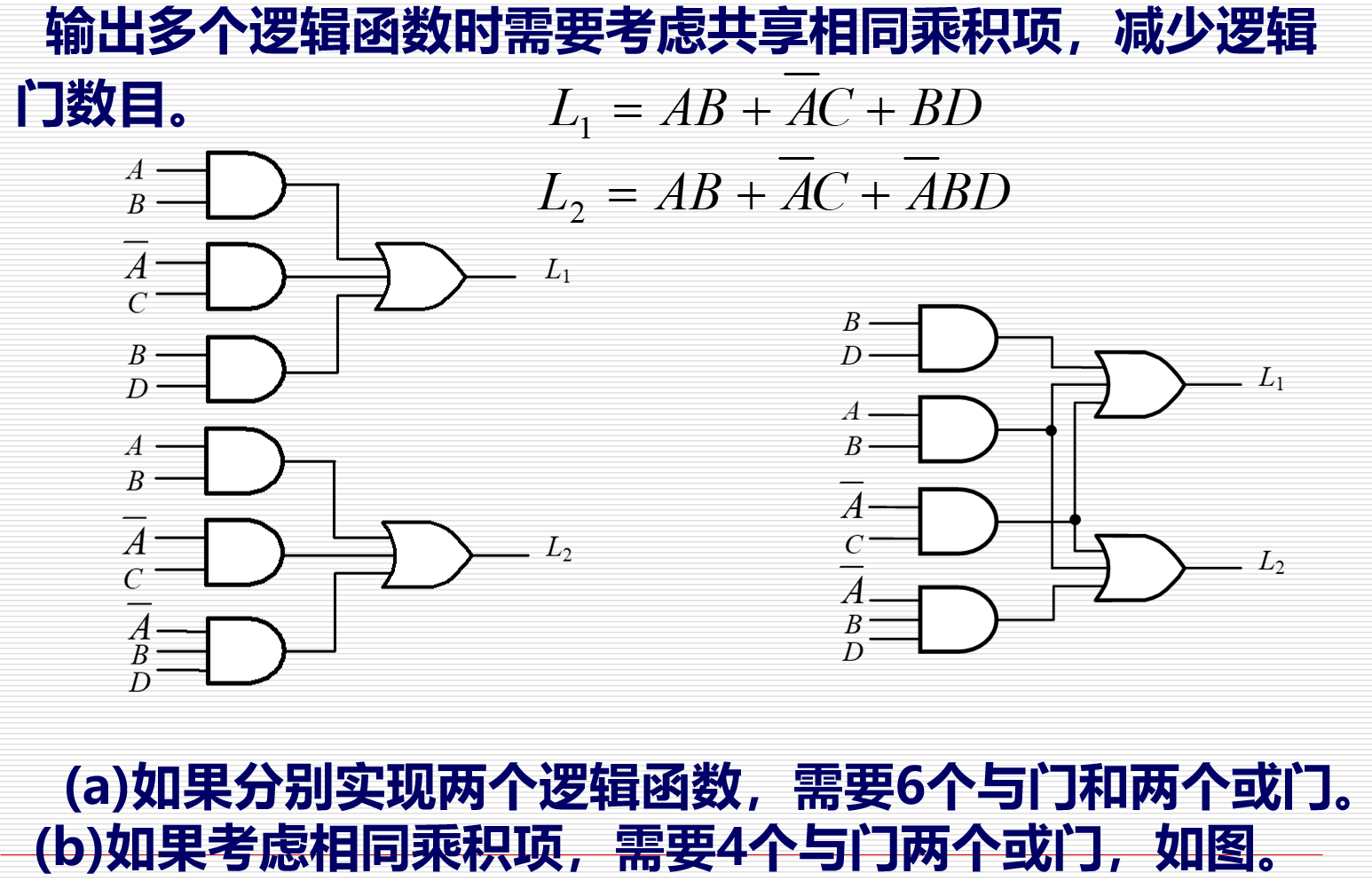 | 见左图文字 |
| 多级逻辑电路(限定入数) | 提取公因项 | 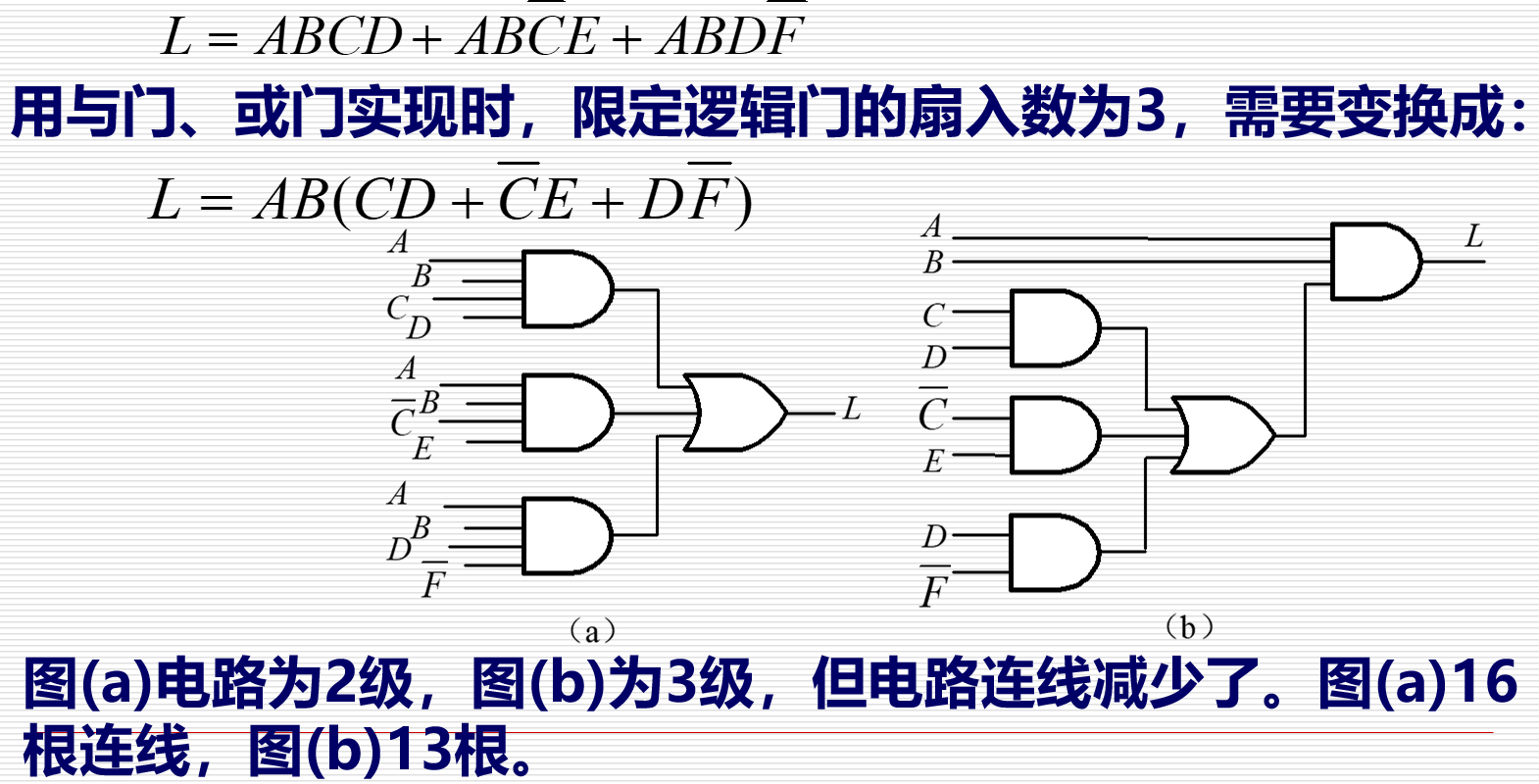 | 见左图文字 |
| 多级逻辑电路(限定入数) | 提取公因项 |  | 见左图文字 |
4.3 组合逻辑电路中的竞争与冒险
4.3.1 产生的原因
门级元件的延时效应
4.3.2 消去的方法
-
消除互补变量
-
增加乘积项,避免互补项相加
-
输出端并联电容器

4.4 若干典型的组合逻辑电路
4.4.1 编码器
普通编码器:只允许有一个输入,从而进行编码,一旦出现多输入就会发生错误
优先编码器:无论多少输入,都会按照一开始设定的优先级进行最高等级的那一个信号位的编码
| 名称 | 型号 | 逻辑符号 | 功能分析 | 逻辑图 |
|---|---|---|---|---|
| 4-2优先编码器 | 74LS00 | 2片7400(4个2输入与非门)实现 | 需要将4-2优先编码器的两个逻辑函数转化为与非式,从而进行电路逻辑的搭建。化简后发现需要7个2输入与非门,故需要2片7400才能实现4-2线优先编码器 | |
| 8-3优先编码器 | CD4532 | 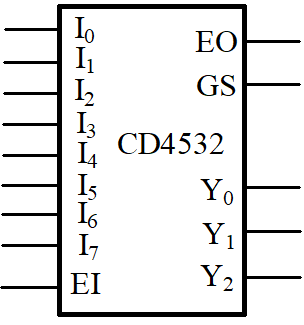 | 除了8个输入端与3个输出端,还有EI、EO与GS端。其中GS是用来标明当前电路是否处于工作状态的,即如果没有输入端为有效信号,GS就是低电平,反之则是高电平。而EI与EO是为了电路扩展而诞生的,当EI为高电平且没有任何输入的情况下,EO也是1,此时的4532就相当于一根导线,从而可以进行片子的扩展 | 由于有现成的集成电路板,故就是逻辑符号 |
| 16-4优先编码器 | CD4532 | 2片4532实现 | 首先确保EI始终为高电平。输出后三位就是两个4532片子的3输出分别或的结果,最高位的输出是高位片的GS端的结果 |  |
| 32-5优先编码器 | 74LS00+CD4532 | 1片7400+4片4532实现 | 首先确保EI始终为高电平。输出后三位就是四个4532片子的3输出分别或的结果,最高位的两个输出取决于4个片子GS端4-2优先编码的结果。 |  |
4.4.2 译码器/数据分配器
| 名称 | 型号 | 逻辑符号 | 功能分析 | 逻辑图 |
|---|---|---|---|---|
| 2-4译码器 | 74X139 |  | 使能端有效时。按照对应的输出给出相应输出的低电平信号 | 由于有现成的集成电路板,故就是逻辑符号 |
| 3-8译码器 | 74X138 |  | 使能端有效时。按照对应的输出给出相应输出的低电平信号 | 由于有现成的集成电路板,故就是逻辑符号 |
| 4-16译码器 | 74X138或74X139 | 2片74X138或5片74X139 | 使能端有效时。输入的前三位分别接入两片3-8译码器的输入端,输入的最后一位接入两片3-8译码器的高电平使能端即可;如果用2-4译码器来实现,输入的前两位分别接入四片2-4译码器的输入端,输入的后两位通过一个2-4译码器的四个输入分别接入4片2-4译码器的低电平使能端即可 |  |
| 5-32译码器 | 74X139+74X138 | 1片74X139+4片74X138 | 使能端有效时。输入的前三位分别接入四片3-8译码器的输入端,输入的后两位通过2-4译码的4个结果分别接入四片3-8译码器的低电平使能端,从而决定是哪一个3-8译码器在工作 |  |
使用译码器实现逻辑函数
我们知道译码器的每一个输出代表一个最小项,那么对于一个 x x x 变量的逻辑函数,可以通过以下步骤用 x ? 2 x x-2^x x?2x 译码器实现任意 x x x 变量的逻辑函数
- 将逻辑函数转化为最小项表达式(大量使用摩根定律)
- 转化为译码器的输出(写成 ∑ m i \sum m_i ∑mi? 的形式)
- 在译码器的输出端加一个多输入与非门即可(对结果进行与非)

数据分配器
功能:相当于多输出的单刀多掷开关,是将公共数据线上的数据按需要送到不同的通道上去的逻辑电路。

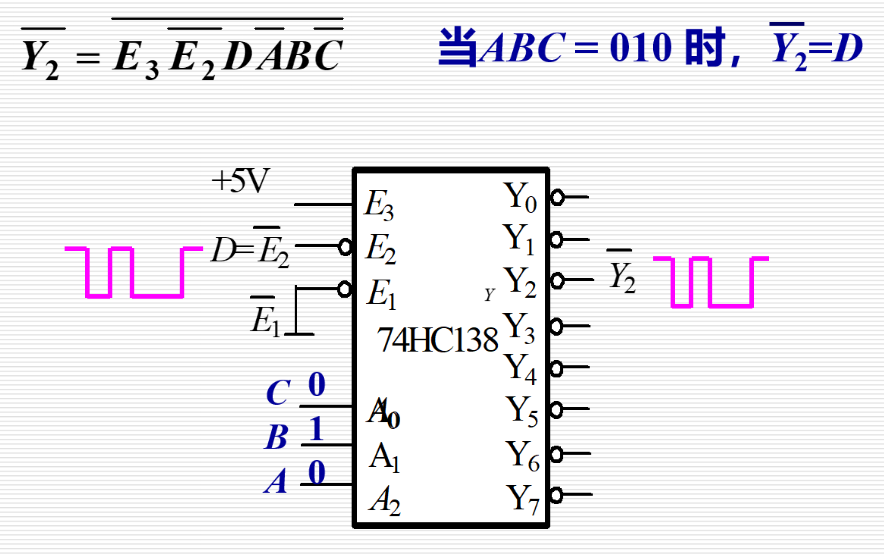
4.4.3 数据选择器
| 名称 | 型号 | 逻辑符号 | 功能分析 | 逻辑图 |
|---|---|---|---|---|
| 2选1 | — | 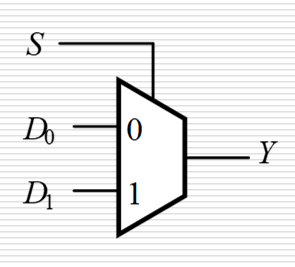 | 通过控制端 S S S 来选择 D 0 , D 1 D_0,D_1 D0?,D1? |  |
| 4选1 | — |  | 通过控制端 S 0 , S 1 S_0,S_1 S0?,S1? 来选择 D 0 , D 1 , D 2 , D 3 D_0,D_1,D_2,D_3 D0?,D1?,D2?,D3? |  |
| 8选1 | 74HC151 |  | 通过控制端 S 0 ? S 2 S_0-S_2 S0??S2? 来选择 D 0 ? D 7 D_0-D_7 D0??D7? | 由于有现成的集成电路板,故就是逻辑符号 |
| 16选1 | 2片74HC151 | — | 通过控制端 S 0 ? S 3 S_0-S_3 S0??S3? 来选择 D 0 ? D 15 D_0-D_{15} D0??D15?,输入的前三位连接三个控制端,输入的最后一位连接两片74151的使能端,其实就是译码器的魔改版,让输出为相应的译码结果的高电平而已 | 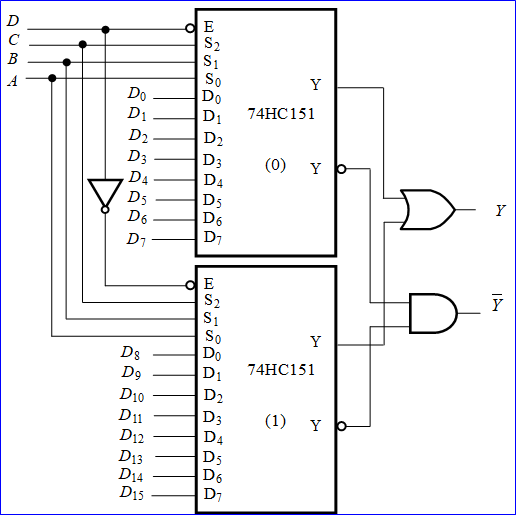 |
使用数据选择器实现逻辑函数
- 变量个数 < < < 数据选择端个数:变量直接对应数据选择端,多余的选择端置0,最后相应的信号输入端进行赋1或赋0的操作即可
- 变量个数 = = = 数据选择端个数:本质上就是将逻辑函数转化为最小项表达式,然后与标准与或式进行比对,已出现的最小项与1,未出现的最小项与0,从而配凑产生了数据选择器最开始的式子。落到逻辑图上就是,数据选择端接入函数变量,信号输入端接入相应的高低电平,出现的最小项就输入1,未出现的就输入0即可
- 变量个数
>
>
> 数据选择端个数:
- 刚好多 1 个:变量 or 变量的非接入信号输入端
- 不止多 1 个:同样采用将变量作为数据信号输入端,此外可能需要借助相关的门电路辅助进行
4.4.4 数值比较器
略
4.4.5 算术运算电路
半加器:即不考虑低位进位的一位二进制加法器。其中
S
S
S 为输出位,
C
C
C 为进位,没有考虑低位的进位
{
S
=
A
⊕
B
C
=
A
B
\begin{cases} S &=& A \oplus B \\ C &=& AB \end{cases}
{SC?==?A⊕BAB?
全加器:即考虑低位进位的一位二进制加法器。其中
S
S
S 为输出位,
C
i
C_i
Ci? 为低位的进位,
C
o
C_o
Co? 为进位
{
S
=
A
⊕
B
⊕
C
i
C
o
=
A
B
+
(
A
⊕
B
)
C
i
=
A
B
+
(
A
+
B
)
C
i
\begin{cases} S &=& A \oplus B \oplus C_i \\ C_o &=& AB + (A \oplus B)C_i = AB+(A+B)C_i \end{cases}
{SCo??==?A⊕B⊕Ci?AB+(A⊕B)Ci?=AB+(A+B)Ci??
4.5 用 verilog 描述组合逻辑电路
五、锁存器和触发器
本章介绍时序逻辑电路的存储单元,分别为锁存器和触发器。其中锁存器对电平敏感,触发器对边沿敏感
5.1 基本双稳态电路
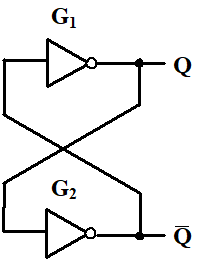
5.2 S R SR SR 锁存器
| 门级元件组成 | 电路图 | 功能分析 |
|---|---|---|
| 或非门实现 | 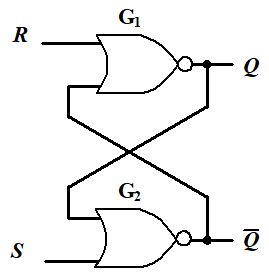 | 高电平有效。全0不变,谁1谁有效,都1不确定状态 |
| 与非门实现 | 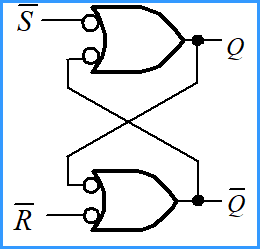 | 低电平有效。全1不变,谁0谁有效,都0不确定状态 |
| 应用 | 电路图 | 功能分析 |
|---|---|---|
| 开关电路 |   | 无论开关如何震动,输出始终正常 |
| 门控 SR 锁存器 |  | 就是加了一个使能端 E,如果 E 为 1,则就是一个基本的 SR 锁存器,如果 E 为 0,则保持 |
5.3 D D D 锁存器
| 电路名称 | 逻辑电路图 | 功能分析 |
|---|---|---|
| 传输门控制的D锁存器 | 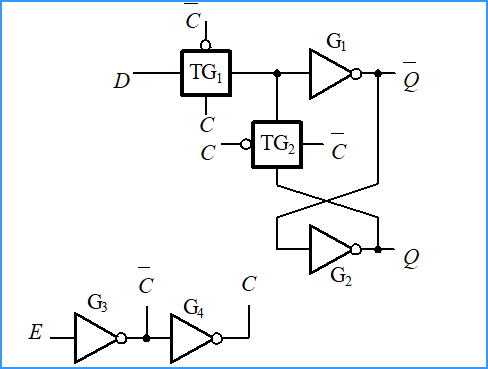 | E=0, Q=不变;E=1, Q=D |
| 逻辑门控制的D锁存器 |  | E=0, Q=不变;E=1, Q=D |
5.4 触发器
5.4.1 主从 D 触发器的电路结构和工作原理
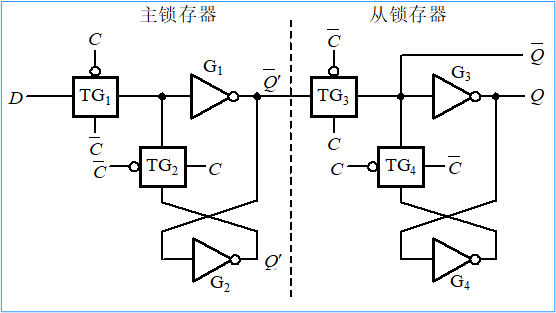
5.4.2 典型的主从 D 触发器集成电路
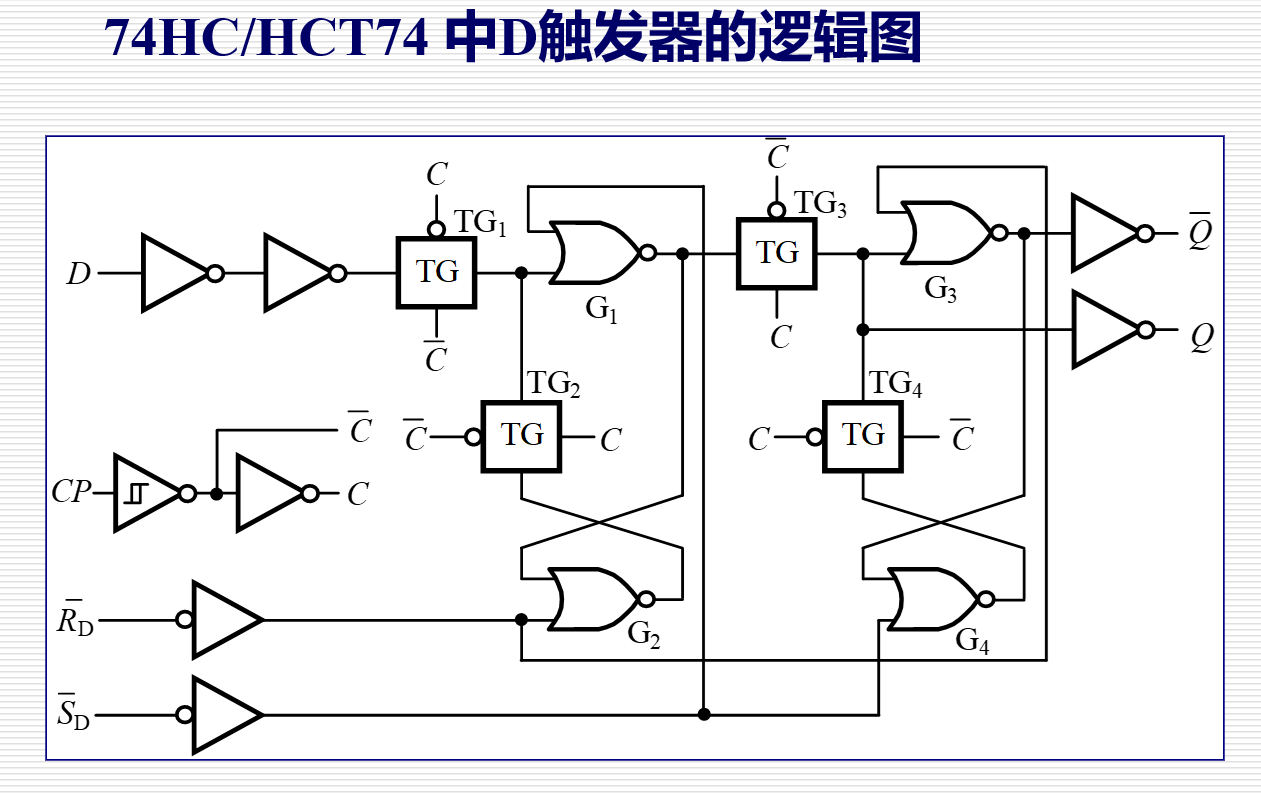

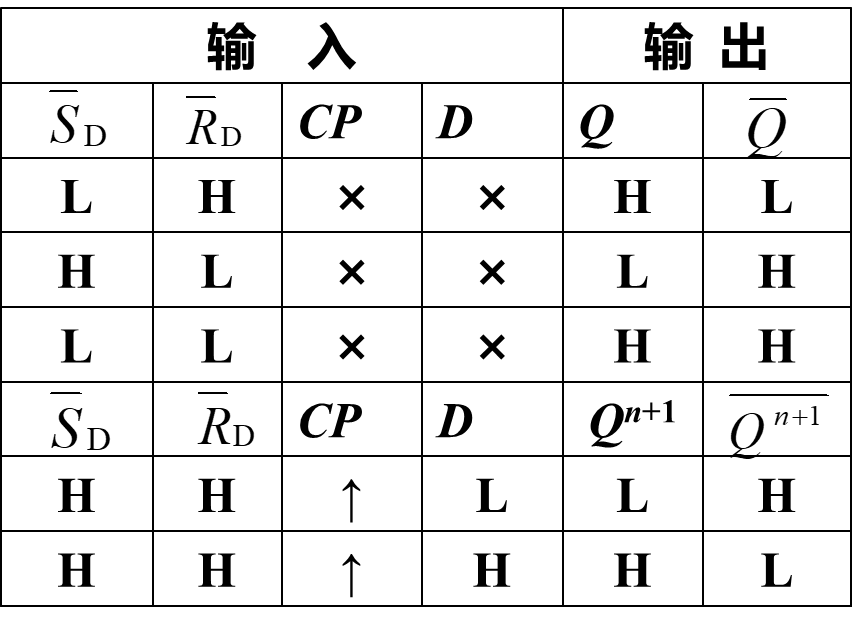
5.5 触发器的逻辑功能
本目需要掌握有关触发器的特性表、特性方程、状态图三者的单独书写以及相互转化的逻辑过程,还需要掌握不同的触发器之间的相互替换实现
| 类型 | 逻辑符号 | 特性表 | 特性方程 | 状态图 |
|---|---|---|---|---|
| D 触发器 |  | 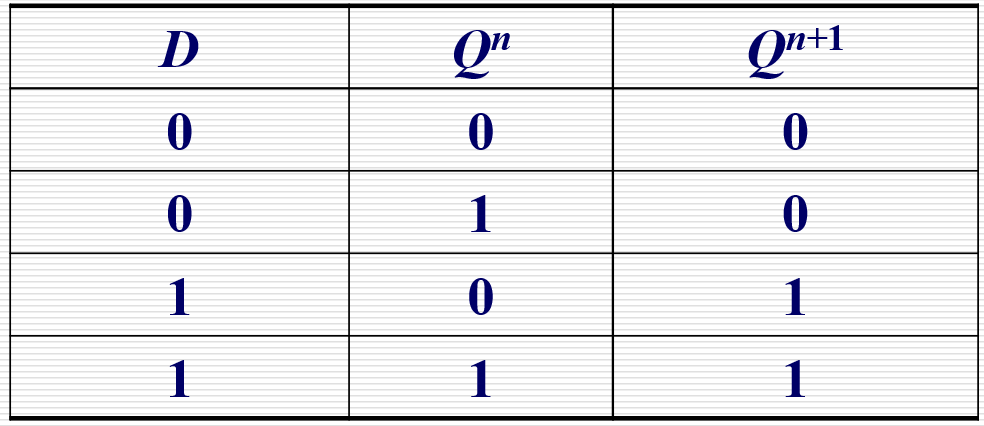 |  | 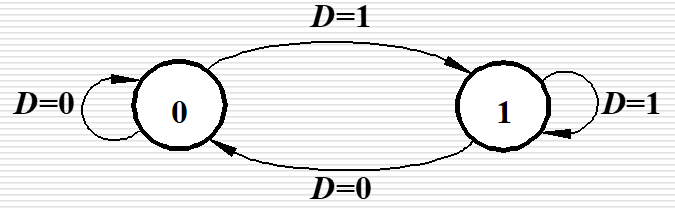 |
| JK 触发器 |  |  |  |  |
| T 触发器 |  |  |  | 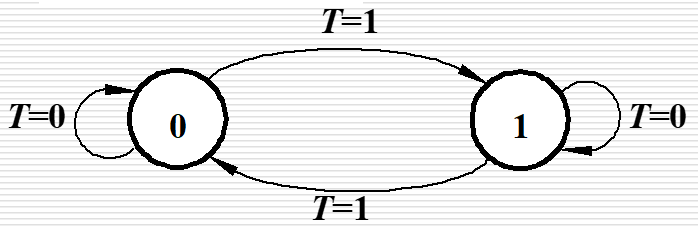 |
| T’ 触发器 | 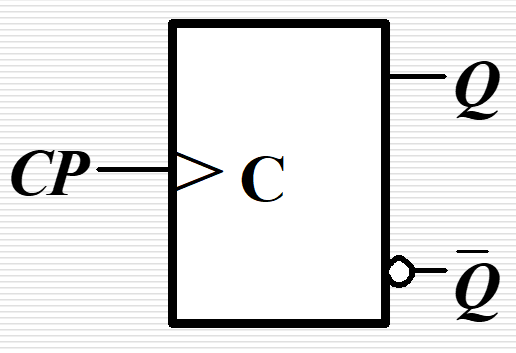 | T ≡ 1 T\equiv 1 T≡1 |  | |
| SR 触发器 |  | 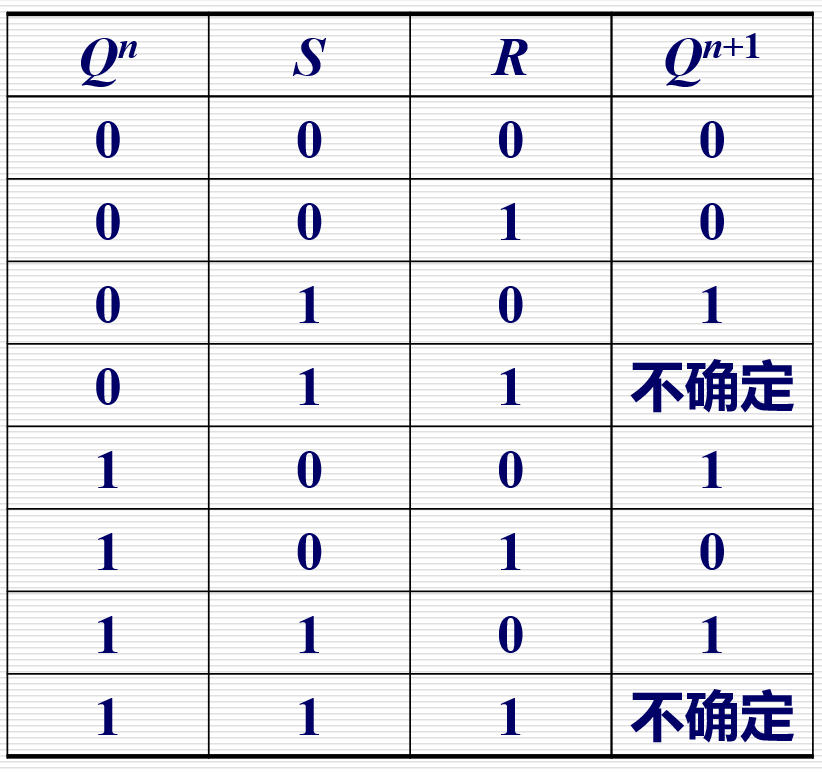 |  |  |
六、时序逻辑电路??
6.1 同步时序逻辑电路的分析
本部分只需要掌握同步时序逻辑电路的分析即可,具体直接从例题出发。三道同步时序逻辑电路分析的例题见教材 P282 ~ P286,分别为
- 例一:可控二进制计数器
- 例二:可控双向二进制计数器
- 例三:脉冲分配器
下面介绍同步时序逻辑电路分析的五个步骤。在分析之前我们要知道我们的最终目标是什么,可以知道,我们分析电路的最终目标是想要量化的确定电路的物理实现的功能,至于如何设计,此处不予讨论。现在给定了一个同步时序逻辑电路的逻辑电路图,接下来我们应该:
-
了解电路组成:同步 or 异步?穆尔型输出(与输入无关) or 米利型输出(与输入有关) or 都有?由什么触发器组成的?触发器类型是上升沿出发 or 下降沿触发?
-
列出三个方程:
-
输出方程:电路的最终输出
-
激励方程:触发器的输入
-
状态方程:触发器的输出(将触发器的输入也就是激励方程代入触发器的特性方程即可)
-
-
写出转换表(分析功能用)
-
写出状态图(分析功能用)
-
写出时序图(分析功能用)默认状态的初值设置为 0
6.2 典型的时序逻辑电路 - 计数器
主要讲 N 位二进制计数器中,利用集成电路板 74 L V C 161 74LVC161 74LVC161 实现的 4 位同步二进制递增计数器。进而引出利用该 4 位计数器实现模 N 计数器的分析与设计思路。同时补充 74 L V C 162 74LVC162 74LVC162 实现的 4 位同步十进制递增计时器,进而引出相关的模 N 设计思路。下面分析 74LVC161 4 位同步二进制递增计数器集成板

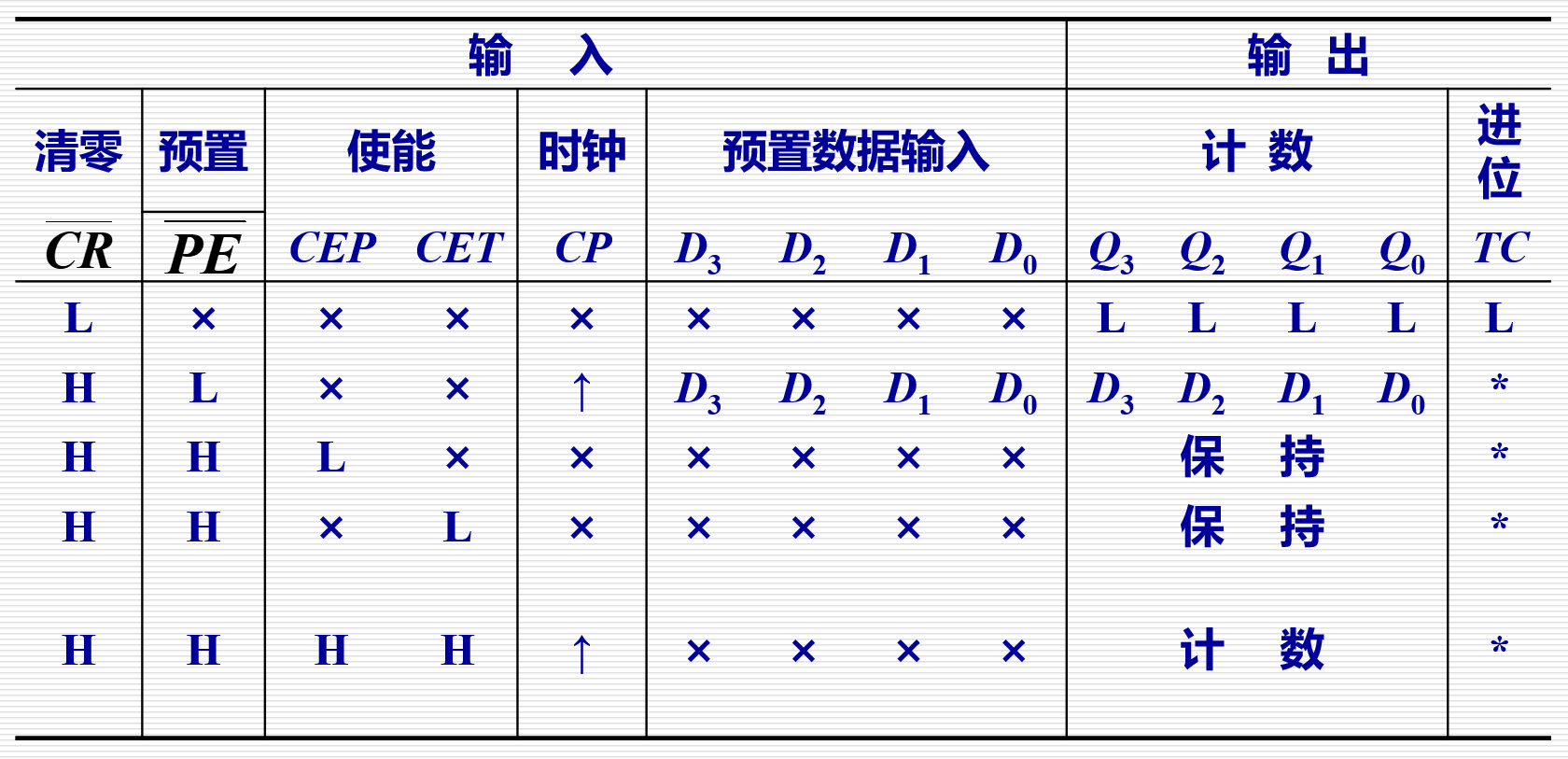
C R  ̄ \overline{CR} CR: 异步清零。即无视时钟脉冲信号,直接清零
P E  ̄ \overline{PE} PE: 同步预置。即当有效始终脉冲沿到来时,实现 4 个预置位的输出,即 D 3 , D 2 , D 1 , D 0 D_3,D_2,D_1,D_0 D3?,D2?,D1?,D0?
C E P , C E T CEP,CET CEP,CET: 使能端。同时为高电平电路才能正常工作
T C TC TC: 进位输出
本目小结
多个集成板进行计数
考虑如何通信:低位进位作为高位使能?
考虑如何清零:同步(异步)清零?同步(异步)置数?
学会利用 74LVC161 的“反馈清零法”实现模 N 计数器
学会利用 74LVC161 的”反馈置数法“实现模 N 计数器
学会实现 74LVC162 十进制递增功能功能(同步清零、同步置数)
学会利用 74LVC162 的同步清零的特性实现模 9 的九进制计数器功能
学会利用 74LVC162 实现模 24 的二十四进制计数器功能
00-09与10-19的计数:通过低位片的进位端,作为高位片的使能端即可
20-23与23-00的计数:通过将低位片的两个低位与高位片通过 4023 三输入与非门连接起来,当全为1时,就是计数到23的状态,此时对高低片进行同步清零即可
6.3 用 verilog 描述同步时序逻辑电路
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!