特征工程之降维算法

数据降维简介

数据降维即对原始数据特征进行变换，使得特征的维度减少。

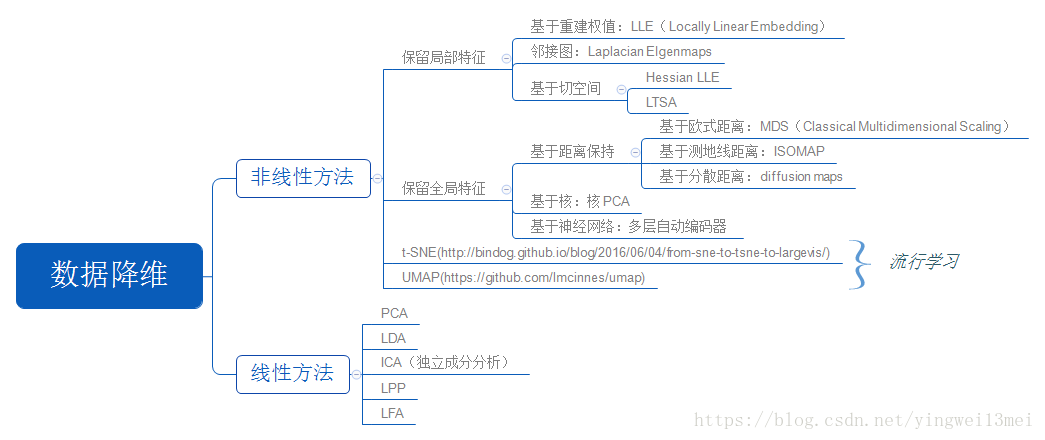
依据降维过程是否可以用一个线性变换表示，降维算法可以分为线性降维算法和非线性降维算法，下图展示了各种降维算法及其类别：

降维的必要性：

1. 多重共线性和预测变量之间相互关联。多重共线性会导致解空间的不稳定，从而可能导致结果的不连贯。
2. 高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间，而在十维空间上只有2%。
3. 过多的变量，对查找规律造成冗余麻烦。
4. 仅在变量层面上分析可能会忽略变量之间的潜在联系。例如几个预测变量可能落入仅反映数据某一方面特征的一个组内。

降维的目的：

1. 减少预测变量的个数。
2. 确保这些变量是相互独立的。
3. 提供一个框架来解释结果。相关特征，特别是重要特征更能在数据中明确的显示出来；如果只有两维或者三维的话，更便于可视化展示。
4. 数据在低维下更容易处理、更容易使用。
5. 去除数据噪声。
6. 降低算法运算开销。

SVD

对于n阶实对称矩阵A，若非零向量x和数