day42 动态规划(4)
发布时间:2024年01月09日
day42
代码随想录
2024.1.9
1. 01背包问题

首先,该dp数组是一个二维数组
- dp[i][j]表示从i-1的物品里任意取,放进容量为j的背包,价值总和最大是多少。
- 知道dp数组的含义,那么,遍历时对于i物品来说,就有两种选择,不放物品i,也就是物品i重量太重了,大于背包j的重量,此时dp[i][j]=dp[i-1][j];第二种选择就是放物品i,此时对于i-1来说,重量就要减少,也就是dp[i-1][j-weight[i]]+value[i],这就是上一个状态的dp值,最后,就是选这两种情况中价值最大的
- 对于dp数组初始化,一个二维数组,首先,j=0,也就是背包为0,那此时肯定价值也是0,因为放不了东西。然后,我们根据递推公式可知i是由i-1得到的,那么i=0就要初始化;那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
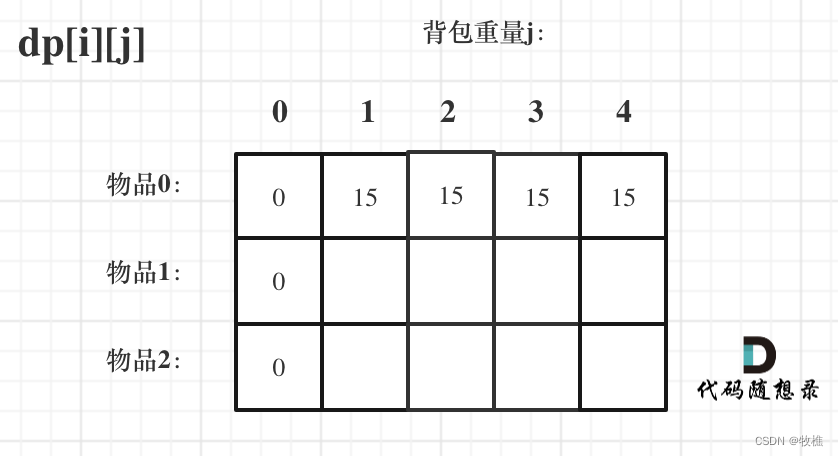
- 遍历顺序则是两种都可以
- 略!
void test_2_wei_bag_problem1() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagweight = 4;
// 二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
}
3. 416分割等和子集
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
// dp[i]中的i表示背包内总和
// 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200
// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了
vector<int> dp(10001, 0);
for (int i = 0; i < nums.size(); i++) {
sum += nums[i];
}
// 也可以使用库函数一步求和
// int sum = accumulate(nums.begin(), nums.end(), 0);
if (sum % 2 == 1) return false;
int target = sum / 2;
// 开始 01背包
for(int i = 0; i < nums.size(); i++) {
for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
// 集合中的元素正好可以凑成总和target
if (dp[target] == target) return true;
return false;
}
};
文章来源:https://blog.csdn.net/qq_56913257/article/details/135477100
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!