代码随想录打卡第二天| 977.有序数组的平方 209.长度最小的子数组 59.螺旋矩阵Ⅱ

977.有序数组的平方（文章链接、视频链接）

1.第一想法将数组平方然后进行快速排序，趁着408的记忆还在给出暴力解。注意递归实现快排的时候内层循环仍需要保持（low<high）为什么？（因为循环结束时内层可能会出现low>=high，虽然此时循环结束，但是内层循环在没有low<high的保护下可能已经完成low>=high情况下的数值覆盖，产生越界错误。）下面给出暴力解法代码实现：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* sortedSquares(int* nums, int numsSize, int* returnSize) {
    int i,j;
    for(i=0;i<numsSize;i++){
        nums[i]=nums[i]*nums[i];
    }
    quicksort(nums,0,numsSize-1);
    *returnSize=numsSize;//确定返回数组大小
    return nums;
}
void quicksort(int A[],int low,int high){//递归实现快排
    if(low<high){
        int pivotpos=partition(A,low,high);
        quicksort(A,low,pivotpos-1);
        quicksort(A,pivotpos+1,high);
    }
}
int partition(int A[],int low,int high){//枢轴划分算法
    int pivot=A[low];
    while(low<high){
        while(low<high&&A[high]>=pivot)
        --high;
        A[low]=A[high];
        while(low<high&&A[low]<=pivot) 
        ++low;
        A[high]=A[low];
    }
    A[low]=pivot;
    return low;
}

2.考虑到暴力算法没有用到数组有序这个条件，考察数组，易知元素平方的最大值只可能在首部或尾部取到（因为有负数），采用双指针，从数组两端向中间移动，下面给出双指针算法实现代码：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* sortedSquares(int* nums, int numsSize, int* returnSize) {
    *returnSize=numsSize;
    int* ans=(int*)malloc(sizeof(int)*numsSize);
    int i=0;
    int j=numsSize-1;
    for(int index=numsSize-1;index>=0;index--){//从数组最后一个位置开始填充
        int isquare=nums[i]*nums[i];
        int jsquare=nums[j]*nums[j];
        if(isquare>jsquare){
            ans[index]=isquare;
            i++;
        }
        else{
            ans[index]=jsquare;
            j--;
        }
    }
    return ans;
}

209.长度最小的子数组（文章讲解、视频讲解）

1.两重循环暴力解，测试用例超时

int minSubArrayLen(int target, int* nums, int numsSize) {
    int minlength=INT_MAX;//定义一个数值很大的整型，方便之后与minlength交换数值
    int i,j,sum;//分别用来定义最小子数组的起始位置
    for(i=0;i<numsSize;i++){
         sum=0;
        for(j=i;j<numsSize;j++){
            sum+=nums[j];
            if(sum>=target){
                int length=j-i+1;//当前子数组长度
                minlength=minlength<length? minlength :length;//更新子数组长度
            }
        }
    }
    return minlength==INT_MAX? 0: minlength;
}

2.滑动窗口解法（虽然是for循环套while循环，但时间复杂度其实是O（n））

int minSubArrayLen(int target, int* nums, int numsSize) {
    int minlength=INT_MAX;//定义一个数值很大的整型，方便之后与minlength交换数值
    int i=0,j=0,sum=0;//分别用来定义最小子数组的起始位置
    for(;j<numsSize;j++){
        sum+=nums[j];
        while(sum>=target){
            int length=j-i+1;
            minlength=minlength<length? minlength :length;
            sum-=nums[i];//滑动窗口精髓，在保持子数组之和大于target的前提下，尝试缩小子数组长度
            i++;//i增大，子数组减小，尝试减小之后的子数组是否依然符合条件
        }
    }
    return minlength==INT_MAX? 0: minlength;
}

59.螺旋矩阵||（文章讲解、视频讲解）

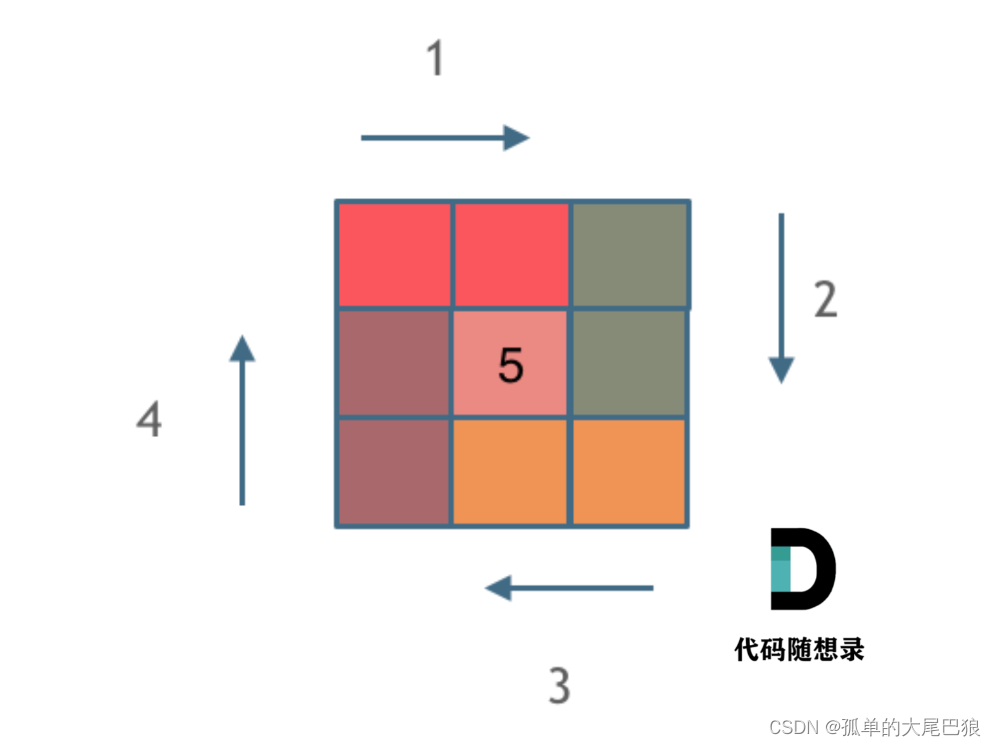
1.没什么思路直接看的讲解，关键是统一处理每条边的逻辑，其次要注意奇数阶矩阵中心元素的单独处理，最后C语言实现代码时注意确定二维数组、一维数组的大小。（附3阶矩阵处理逻辑，一种颜色代表对该行或该列的边界处理）

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** generateMatrix(int n, int* returnSize, int** returnColumnSizes) {
    *returnSize=n;//数组的大小
    *returnColumnSizes=(int*)malloc(sizeof(int*)*n);//指针数组的大小
    int **ans=(int**)malloc(sizeof(int**)*n);//要返回的二维数组
    int i;
    for(i=0;i<n;i++){
        ans[i]=(int*)malloc(sizeof(int)*n);
        (*returnColumnSizes)[i]=n;
    }
    int startX=0;
    int startY=0;
    int mid=n/2;
    int loop=n/2;
    int offset=1;
    int count=1;
    while(loop--){
        int i=startX;
        int j=startY;
        for(j=startY;j<n-offset;j++)
        ans[i][j]=count++;
        for(i=startX;i<n-offset;i++)
        ans[i][j]=count++;
        for(;j>startY;j--)
        ans[i][j]=count++;
        for(;i>startX;i--)
        ans[i][j]=count++;
        startX++;
        startY++;
        offset++;
    }
    if(n%2==1)
    ans[mid][mid]=count;
    return ans;
}

今日总结：如履薄冰。