机器学习扩散模型简介

发布时间：2024年01月13日

一、说明??

????????扩散模型的迅速崛起是过去几年机器学习领域最大的发展之一。在这本易于理解的指南中了解您需要了解的有关扩散模型的所有信息。

????????扩散模型是生成模型，在过去几年中越来越受欢迎，这是有充分理由的。仅在 2020 年代发布的几篇开创性论文就向世界展示了 Diffusion 模型的能力，例如在图像合成方面击败 GAN?[?6?]。最近，从业者将看到DALL-E 2（OpenAI 上个月发布的图像生成模型）中使用的扩散模型。

DALL-E 2 生成的各种图像（来源）。

????????鉴于扩散模型最近的成功浪潮，许多机器学习从业者肯定对其内部工作原理感兴趣。在本文中，我们将研究扩散模型的理论基础，然后演示如何在 PyTorch 中使用扩散模型生成图像。如需对扩散模型进行技术性较低、更直观的解释，请随时查看我们关于物理学如何推进生成式 AI 的文章。让我们深入了解吧！

二、扩散模型 - 简介

????????扩散模型是生成模型，这意味着它们用于生成与训练数据相似的数据。?从根本上讲，扩散模型的工作原理是通过连续添加高斯噪声来破坏训练数据，然后学习通过逆转该噪声过程来恢复数据。训练后，我们可以使用扩散模型来生成数据，只需将随机采样的噪声传递到学习的去噪过程中即可。

扩散模型可用于从噪声生成图像（改编自源）

????????更具体地说，扩散模型是使用固定马尔可夫链映射到潜在空间的潜在变量模型。该链逐渐向数据添加噪声以获得近似后验 $q(\textbf{x}_{1:T}|\textbf{x}_0)$ ?，在这里 $\textbf{x}_1, ... , \textbf{x}_T$ ?时间是具有相同维度的潜在变量 $X_0$ 。在下图中，我们看到了图像数据的马尔可夫链。

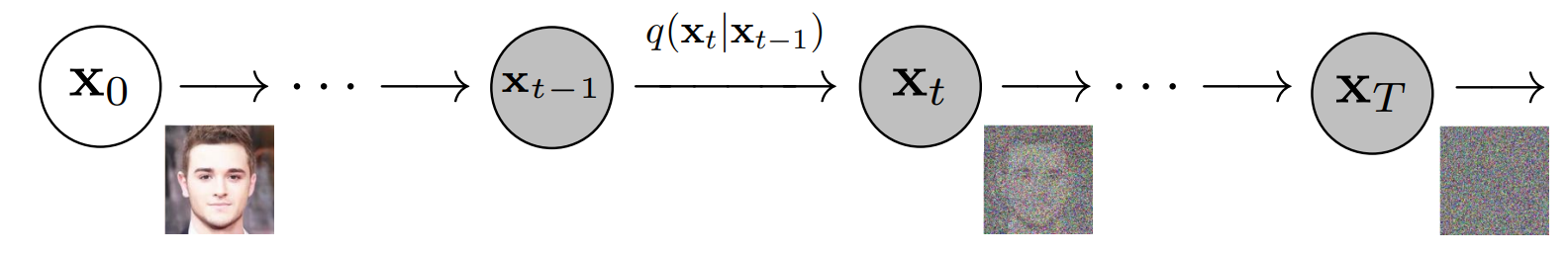
（根据源码修改）

????????最终，图像渐近变换为纯高斯噪声。训练扩散模型的目标是学习相反的过程 - 即训练 $p_\theta(x_{t-1}|x_t)$ 。通过沿着这条链向后遍历，我们可以生成新的数据。

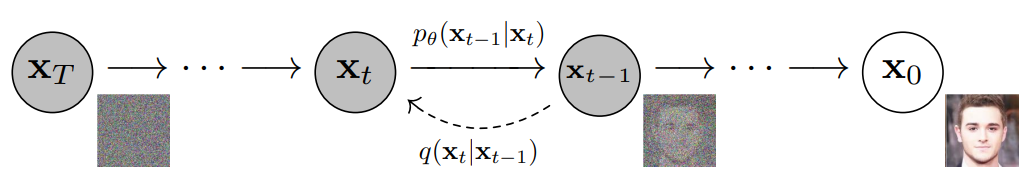
（根据源码修改）

2.1 扩散模型的好处

????????如上所述，近年来对扩散模型的研究呈爆炸式增长。受非平衡热力学[?1?]的启发，扩散模型目前可产生最先进的图像质量，其示例如下：

（改编自来源）

????????除了尖端的图像质量之外，扩散模型还具有许多其他优点，包括不需要对抗性训练。对抗性训练的困难是有据可查的；而且，如果存在具有可比性能和训练效率的非对抗性替代方案，通常最好利用它们。在训练效率方面，扩散模型还具有可扩展性和并行性的额外优势。

????????虽然扩散模型几乎似乎是凭空产生结果，但有许多仔细且有趣的数学选择和细节为这些结果提供了基础，并且最佳实践仍在文献中不断发展。现在让我们更详细地了解一下支持扩散模型的数学理论。

2.2?扩散模型 - 深入探讨

????????如上所述，扩散模型由前向过程（或扩散过程）和反向过程（或反向扩散过程）组成，其中数据（通常是图像）逐渐被噪声化，其中噪声被转换回来自目标分布的样本。

????????当噪声水平足够低时，前向过程中的采样链转换可以设置为条件高斯。将此事实与马尔可夫假设相结合，得出前向过程的简单参数化：

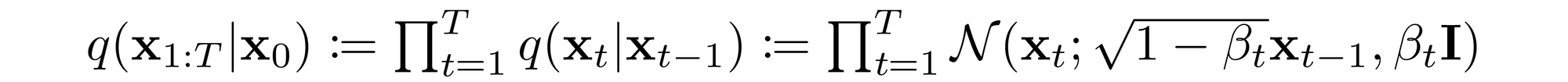
????????数学笔记

????????在这里 $\beta_1, ..., \beta_T$ 时间是一个方差表（学习的或固定的），如果表现良好，可以确保? $x_T$ 时间?对于足够大的 T ，几乎是各向同性高斯分布。

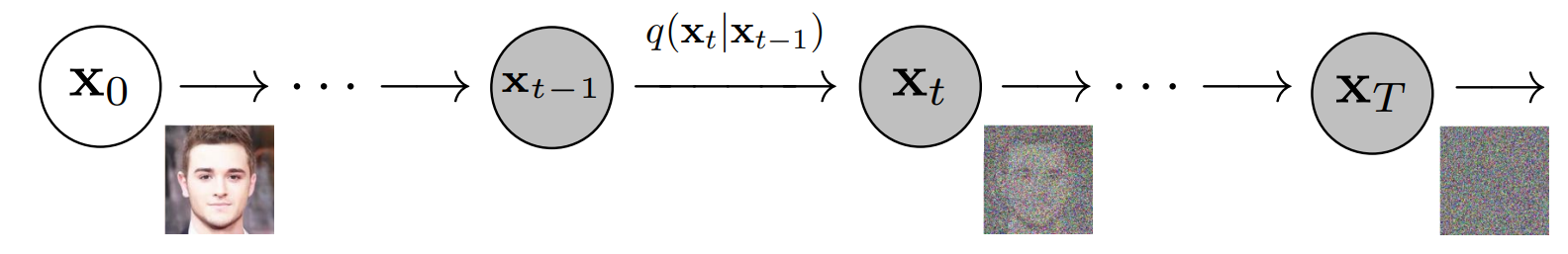
给定马尔可夫假设，潜在变量的联合分布是高斯条件链转换的乘积（从源修改）。

????????如前所述，扩散模型的“魔力”来自于相反的过程。在训练过程中，模型学习扭转这种扩散过程以生成新数据。从纯高斯噪声开始 $p(\textbf{x}_{T}) := \mathcal{N}(\textbf{x}_T, \textbf{0}, \textbf{I})$ ，模型学习联合分布 $p_\theta(\textbf{x}_{0:T})$ 作为

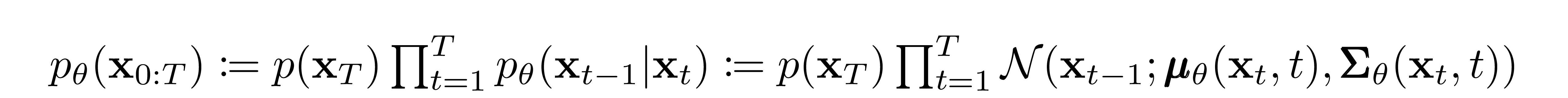
????????其中学习高斯跃迁的时间相关参数。特别注意，马尔可夫公式断言给定的反向扩散转移分布仅取决于前一个时间步（或后一个时间步，取决于您如何看待它）：

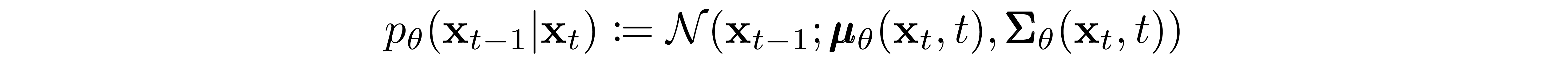
（根据源码修改）

想要了解如何在 PyTorch 中构建扩散模型？

????????查看我们的 MinImagen 项目，我们在其中构建了文本到图像模型 Imagen 的最小实现！

2.3 训练

????????通过寻找使训练数据的可能性最大化的逆马尔可夫转移来训练扩散模型。实际上，训练等效地包括最小化负对数似然的变分上限。

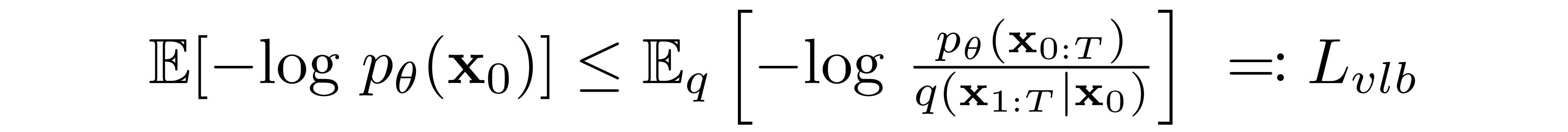
符号详细信息

我们寻求重写 $L_{vlb}$ 我乙就Kullback-Leibler (KL) 散度而言。KL 散度是一种不对称统计距离度量，衡量一个概率分布P与参考分布Q的差异程度。我们有兴趣制定 $L_{vlb}$ ? 就 KL 散度而言，因为我们的马尔可夫链中的转移分布是高斯分布，并且高斯分布之间的 KL 散度具有闭合形式。

2.4 什么是 KL 散度？

连续分布的 KL 散度的数学形式为

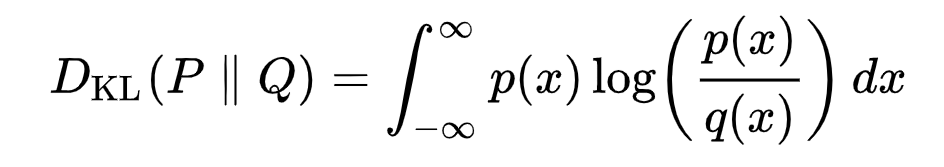
双条表示该函数相对于其参数不对称。

????????下面您可以看到变化分布P（蓝色）与参考分布Q（红色）的 KL 散度。绿色曲线表示上述 KL 散度定义中积分内的函数，曲线下的总面积表示任意给定时刻 ?P与Q的 KL 散度值，该值也以数字形式显示。

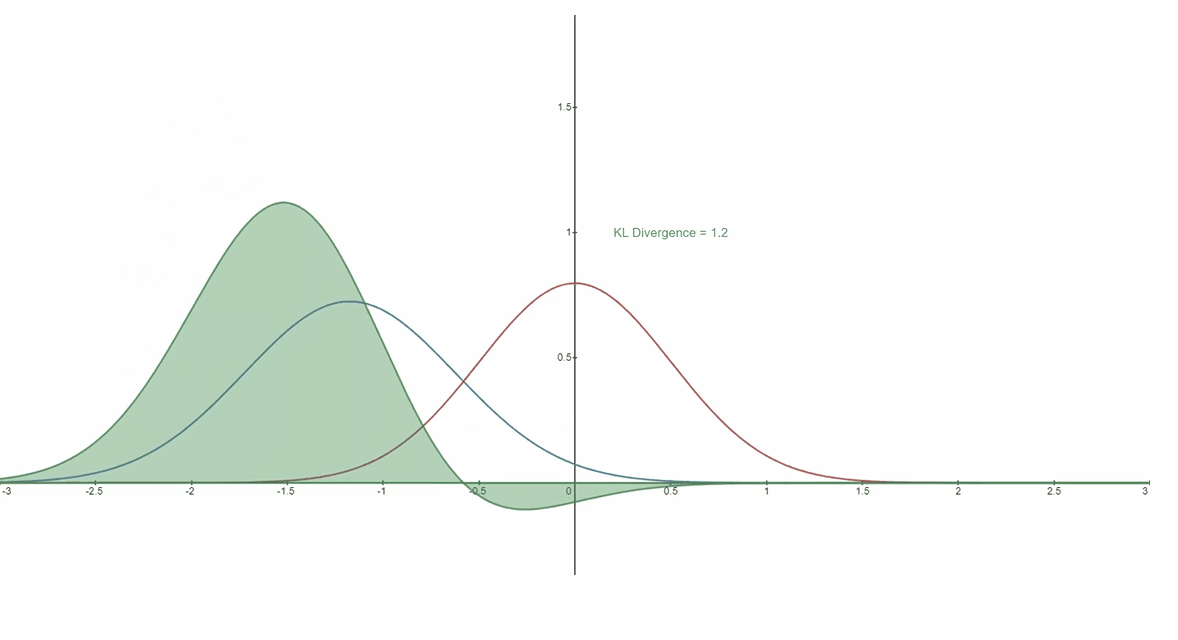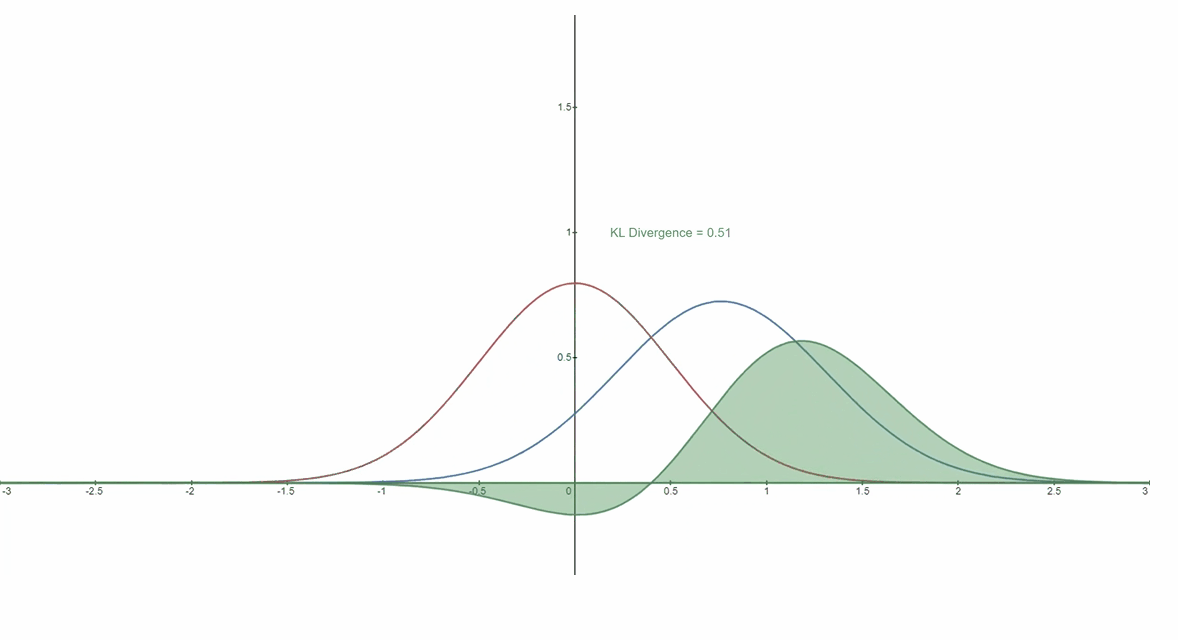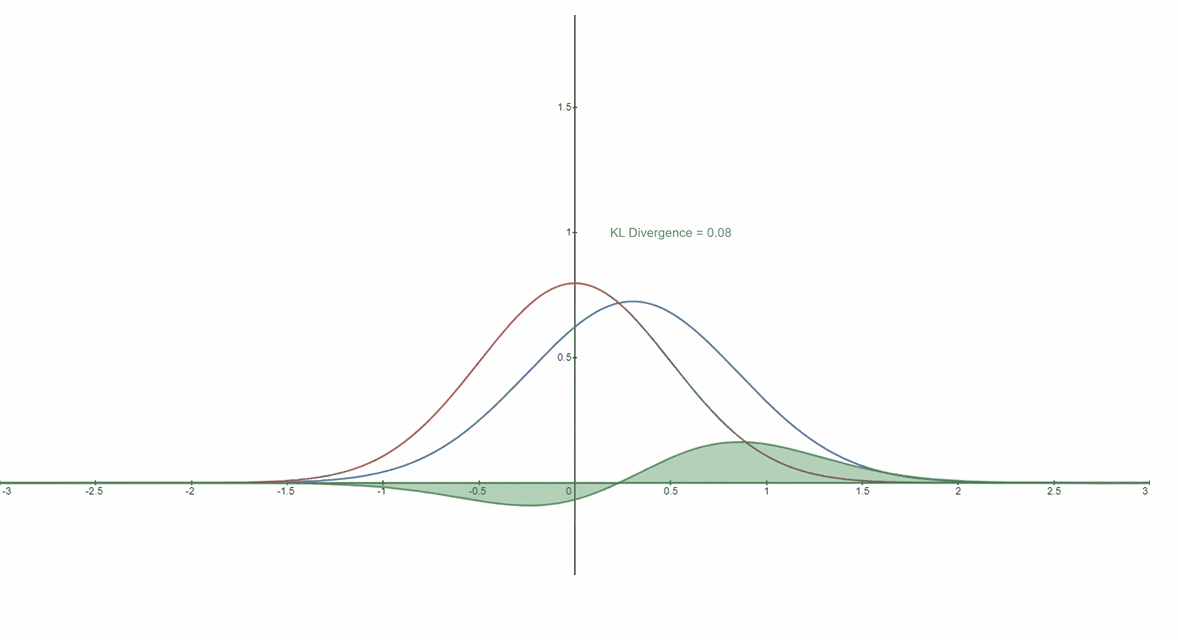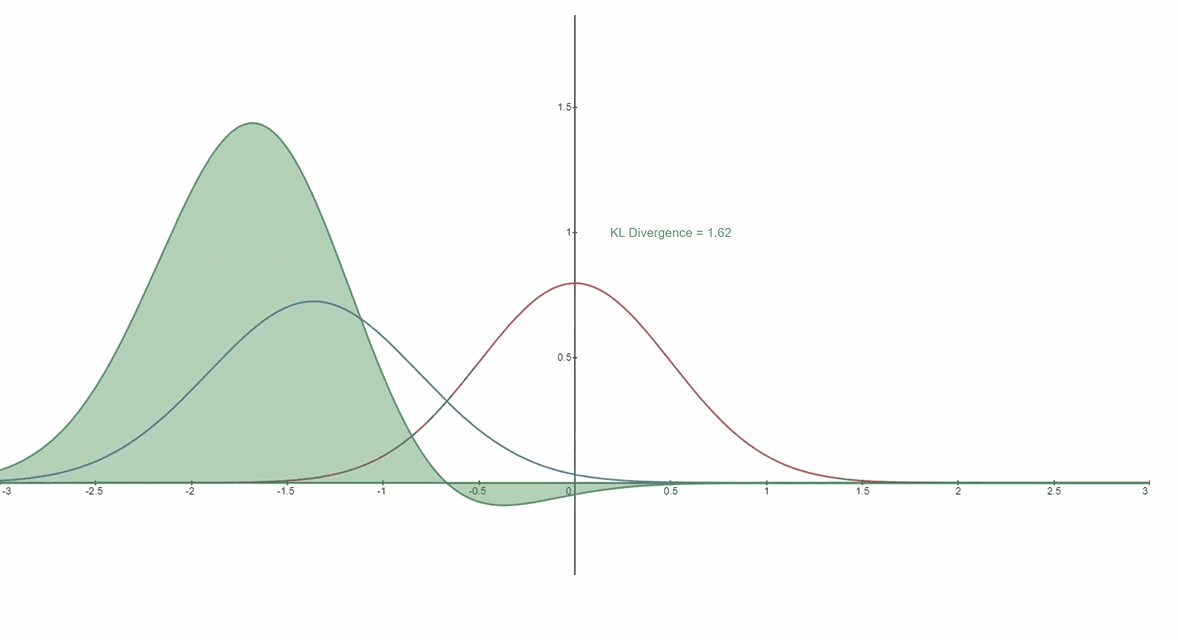
????????铸件 $L_{vlb}$ 依照 KL 散度而言

????????如前所述， [?1?]几乎完全可以重写 $L_{vlb}$ ，就KL 散度而言：

????????在这里

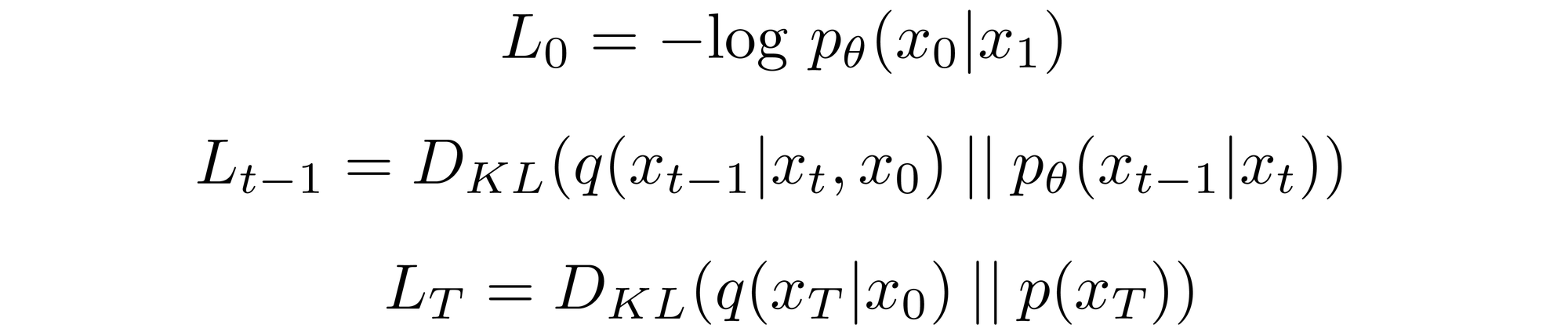
????????推导详情

????????调节后向过程 $x_0$ ?在 $L_{t-1}$ ?结果是一种易于处理的形式，导致所有 KL 散度都是高斯分布之间的比较。这意味着可以使用封闭式表达式而不是蒙特卡罗估计来精确计算散度[?3?]。

2.5 型号选择

????????建立了目标函数的数学基础后，我们现在需要就如何实现扩散模型做出一些选择。对于正向过程，唯一需要的选择是定义方差表，其值通常在正向过程中增加。

????????对于相反的过程，我们更多地选择高斯分布参数化/模型架构。请注意扩散模型提供的高度灵活性- 我们架构的唯一要求是其输入和输出具有相同的维度。

????????我们将在下面更详细地探讨这些选择的细节。

????????转发过程和? $L_T$

????????如上所述，关于前向过程，我们必须定义方差表。特别是，我们将它们设置为与时间相关的常数，忽略了它们是可以学习的事实。例如[?3?]，一个线性时间表 $\beta_1=10^{-4}$ 到 $\beta_T=0.2$ 可能会使用，或者可能是几何级数。

????????无论选择什么特定值，方差表是固定的这一事实会导致 $L_{T}$ 就我们的一组可学习参数而言，它成为一个常数，使我们能够在训练时忽略它。

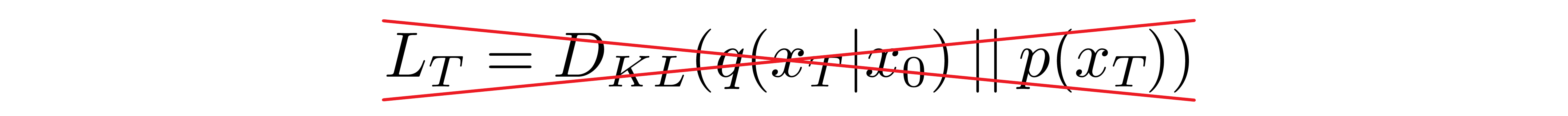
逆向过程和 $L_{1:T-1}$

现在我们讨论定义逆过程所需的选择。回想一下上面我们将逆马尔可夫转移定义为高斯：

????????我们现在必须定义函数形式 $\pmb{\mu}_\theta$ 或者 $\pmb{\Sigma}_\theta$ 。虽然有更复杂的参数化方法 $\pmb{\Sigma}_\theta$ ，我们简单设置

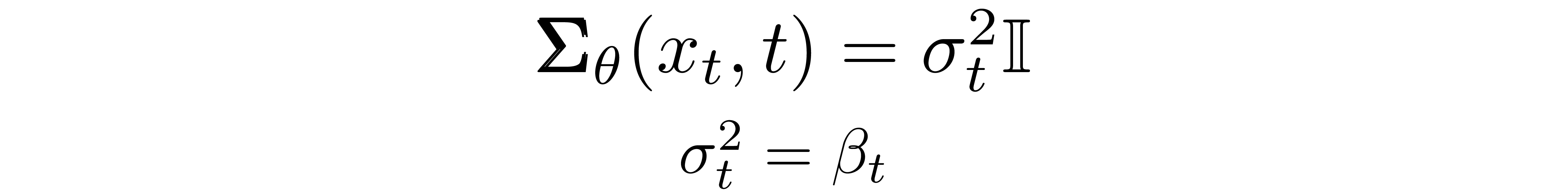
????????也就是说，我们假设多元高斯是具有相同方差的独立高斯的乘积，方差值可以随时间变化。我们将这些方差设置为等于我们的前向过程方差表。

????????鉴于这个新的配方 $\pmb{\Sigma}_\theta$ ，我们有

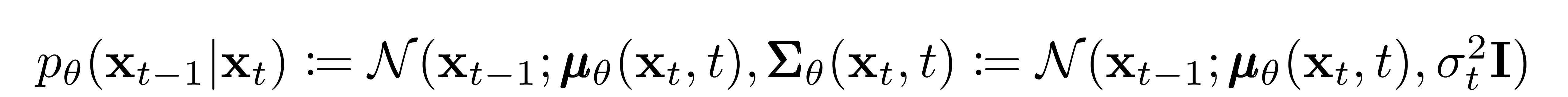
这使我们能够转变

到

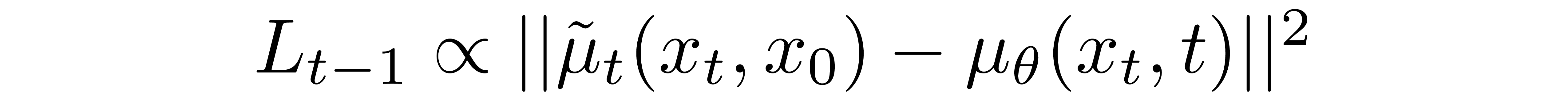
????????其中差值的第一项是以下项的线性组合 $x_t$ 和 $x_0$ 这取决于差异表 $\beta_t$ 。该函数的确切形式与我们的目的无关，但可以在[?3?]中找到。

????????上述比例的意义在于，最直接的参数化 $\mu_\theta$ 简单地预测扩散后验平均值。重要的是，[ 3?]的作者实际上发现训练 $\mu_\theta$ 预测任何给定时间步长的噪声分量会产生更好的结果。特别地，让

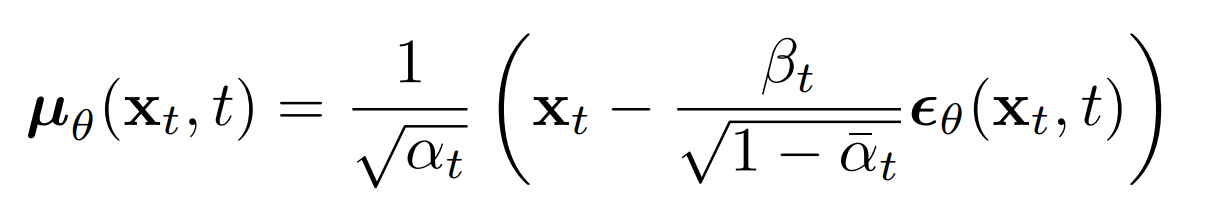
????????在这里

????????这导致了以下替代损失函数，[?3?]的作者发现它可以带来更稳定的训练和更好的结果：

[ 3?]的作者还注意到扩散模型的这种表述与基于 Langevin 动力学的分数匹配生成模型的联系。事实上，扩散模型和基于分数的模型似乎可能是同一枚硬币的两面，类似于基于波的量子力学和基于矩阵的量子力学的独立和同时发展，揭示了相同现象的两种等效公式[?2?]?]。

2.6 网络架构

????????虽然我们的简化损失函数旨在训练模型 $\pmb{\epsilon}_\theta$ ?，我们还没有定义这个模型的架构。请注意，模型的唯一要求是其输入和输出维度相同。

????????考虑到这一限制，图像扩散模型通常采用类似 U-Net 的架构来实现，这也许并不奇怪。

U-Net的架构（来源）

2.7 逆向过程解码器和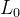 $L_0$ ?

????????逆过程的路径由连续条件高斯分布下的许多变换组成。在反向过程结束时，回想一下我们正在尝试生成一个由整数像素值组成的图像。因此，我们必须设计一种方法来获取所有像素上每个可能像素值的离散（对数）似然。

????????完成此操作的方法是将反向扩散链中的最后一个转换设置为独立的离散解码器。确定给定图像的可能性 $x_0$ 给定 $x_1$ ?，我们首先在数据维度之间施加独立性：

????????其中D是数据的维数，上标i表示提取一个坐标。现在的目标是确定给定像素的每个整数值的可能性有多大，给定时间点轻微噪声图像中相应像素的可能值的分布 $t=1$ ?：

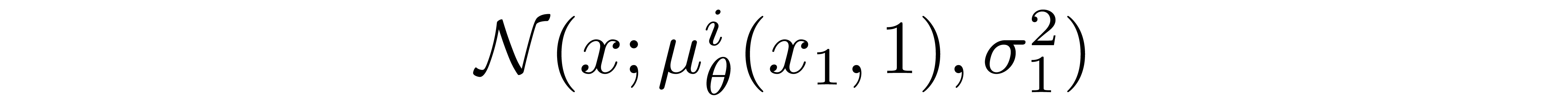
????????其中像素分布 $t=1$ ?源自以下多元高斯，其对角协方差矩阵允许我们将分布拆分为单变量高斯的乘积，一个对应于数据的每个维度：

????????我们假设图像由整数组成 ${0, 1, ..., 255}$ ?（与标准 RGB 图像一样）已线性缩放至[-1,1]。然后，我们将实际线分解为小“桶”，其中，对于给定的缩放像素值x，该范围的桶是 $[x-1/255, x+1/255]$ 。给定相应像素的单变量高斯分布，像素值 x的概率 $x_1$ ，是以x为中心的桶内单变量高斯分布下的面积。

????????下面您可以看到每个桶的面积及其均值为 0 高斯的概率，在这种情况下，对应于平均像素值为255/2（一半亮度）。红色曲线表示t=1图像中特定像素的分布，面积给出了t=0图像中对应像素值的概率。

????????技术说明

????????给定每个像素的t=0像素值，则 $p_\theta(x_0 | x_1)$ ?只是他们的产品。该过程由以下等式简洁地概括：

????????在这里

????????和

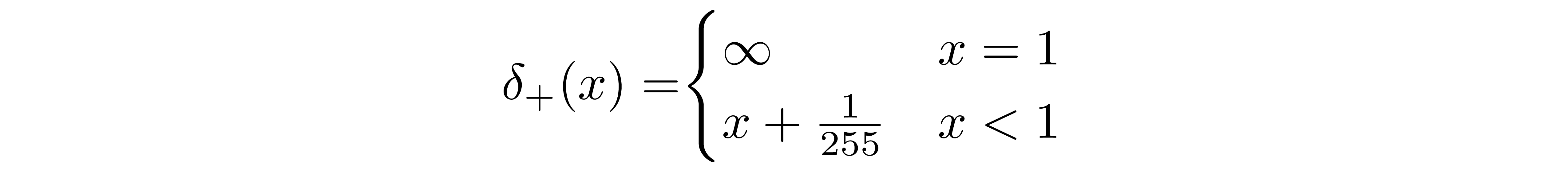
给定这个方程 $p_\theta(x_0 | x_1)$ ?，我们可以计算出最后一项 $L_{vlb}$ ? 它没有被表述为 KL 散度：

2.8 最终目标

正如上一节中提到的，[ 3?]的作者发现在给定时间步长预测图像的噪声分量会产生最佳结果。最终，他们使用以下目标：

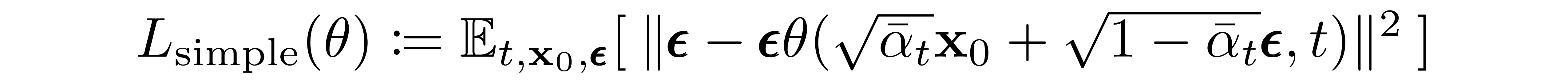
因此，我们的扩散模型的训练和采样算法可以在下图中简洁地描述：

（来源）

三、扩散模型理论总结

????????在本节中，我们详细介绍了扩散模型的理论。我们很容易陷入数学细节中，因此我们在下面的本节中记下最重要的几点，以便从鸟瞰的角度保持方向：

我们的扩散模型被参数化为马尔可夫链，这意味着我们的潜在变量 $x_1, ... , x_T$ ?时间仅取决于前一个（或后一个）时间步长。
马尔可夫链中的转移分布是高斯分布，其中前向过程需要方差调度，而反向过程参数是学习的。
扩散过程确保 $x_T$ 时间对于足够大的 T，渐近分布为各向同性高斯分布。
在我们的例子中，方差表是固定的，但它也是可以学习的。对于固定的时间表，遵循几何级数可能比线性级数提供更好的结果。在任何一种情况下，方差通常都会随着系列中的时间而增加（ $\beta_i < \beta_j$ ?随着 $i < j$ ）。
扩散模型非常灵活，允许使用输入和输出维度相同的任何架构。许多实现都使用类似 U-Net 的架构。
训练目标是最大化训练数据的?可能性。?这表现为调整模型参数以最小化数据的负对数似然的变分上限。
由于我们的马尔可夫假设，目标函数中的几乎所有项都可以转换为KL 散度。鉴于我们使用的是高斯分布，这些值变得可以计算，因此省略了执行蒙特卡洛近似的需要。
最终，使用简化的训练目标来训练预测给定潜在变量的噪声分量的函数会产生最佳且最稳定的结果。
作为反向扩散过程的最后一步，离散解码器用于获取像素值的对数似然。

????????了解了扩散模型的高级概述后，让我们继续了解如何在 PyTorch 中使用扩散模型。

四、PyTorch 中的扩散模型

????????虽然扩散模型尚未像机器学习中的其他旧架构/方法那样民主化，但仍然有可用的实现。在 PyTorch 中使用扩散模型的最简单方法是使用该denoising-diffusion-pytorch包，它实现了像本文中讨论的图像扩散模型。要安装该软件包，只需在终端中输入以下命令：

pip install denoising_diffusion_pytorch

4.1 最小的例子

为了训练模型并生成图像，我们首先导入必要的包：

import torch
from denoising_diffusion_pytorch import Unet, GaussianDiffusion

????????接下来，我们定义网络架构，在本例中是 U-Net。该dim参数指定第一次下采样之前的特征图数量，该dim_mults参数提供该值和后续下采样的被乘数：

model = Unet(
    dim = 64,
    dim_mults = (1, 2, 4, 8)
)

????????现在我们的网络架构已经定义，我们需要定义扩散模型本身。我们传入刚刚定义的 U-Net 模型以及几个参数 - 要生成的图像的大小、扩散过程中的时间步数以及 L1 和 L2 范数之间的选择。

diffusion = GaussianDiffusion(
    model,
    image_size = 128,
    timesteps = 1000,   # number of steps
    loss_type = 'l1'    # L1 or L2
)

????????现在已经定义了扩散模型，是时候进行训练了。我们生成随机数据进行训练，然后以通常的方式训练扩散模型：

training_images = torch.randn(8, 3, 128, 128)
loss = diffusion(training_images)
loss.backward()

????????一旦模型训练完成，我们最终就可以使用对象sample()的方法生成图像diffusion。这里我们生成 4 张图像，考虑到我们的训练数据是随机的，这些图像只是噪声：

sampled_images = diffusion.sample(batch_size = 4)

4.2 自定义数据培训

????????该denoising-diffusion-pytorch包还允许您在特定数据集上训练扩散模型。只需将'path/to/your/images'字符串替换为下面对象中的数据集目录路径Trainer()，然后更改image_size为适当的值即可。之后，只需运行代码来训练模型，然后像以前一样进行采样。请注意，PyTorch 必须在启用 CUDA 的情况下进行编译才能使用该类Trainer：

from denoising_diffusion_pytorch import Unet, GaussianDiffusion, Trainer

model = Unet(
    dim = 64,
    dim_mults = (1, 2, 4, 8)
).cuda()

diffusion = GaussianDiffusion(
    model,
    image_size = 128,
    timesteps = 1000,   # number of steps
    loss_type = 'l1'    # L1 or L2
).cuda()

trainer = Trainer(
    diffusion,
    'path/to/your/images',
    train_batch_size = 32,
    train_lr = 2e-5,
    train_num_steps = 700000,         # total training steps
    gradient_accumulate_every = 2,    # gradient accumulation steps
    ema_decay = 0.995,                # exponential moving average decay
    amp = True                        # turn on mixed precision
)

trainer.train()

下面您可以看到从多元高斯噪声到 MNIST 数字的渐进式去噪，类似于反向扩散：

五、最后的话

????????扩散模型是一种概念上简单而优雅的方法来解决数据生成问题。他们最先进的成果与非对抗性训练相结合，将他们推向了很高的高度，鉴于其刚刚起步的地位，预计未来几年将取得进一步的进步。特别是，扩散模型被发现对于DALL-E 2等尖端模型的性能至关重要。

#参考

[6]扩散模型在图像合成方面击败了 GAN

[7]?GLIDE：使用文本引导扩散模型实现真实感图像生成和编辑

[8]使用 CLIP Latents 生成分层文本条件图像

【9】Introduction to Diffusion Models for Machine Learning (assemblyai.com)?

文章来源:https://blog.csdn.net/gongdiwudu/article/details/135543397
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

机器学习扩散模型简介

一、说明??

二、扩散模型 - 简介

2.1 扩散模型的好处

2.2?扩散模型 - 深入探讨

2.3 训练

2.4 什么是 KL 散度？

2.5 型号选择

2.6 网络架构

2.7 逆向过程解码器和?

2.8 最终目标

三、扩散模型理论总结

四、PyTorch 中的扩散模型

4.1 最小的例子

4.2 自定义数据培训

五、最后的话

#参考

2.7 逆向过程解码器和 $L_0$ ?