我记不住的那些位操作bitwise(一)

背景： 最近在看底层的一些知识内容，其中有一些位操作，所以想复习并记录一下。

一、或

或：? ?0 |? 1 = 1? 及? 1 | 1 =1? ?但是无法区分这两种情况(1. 一个是false，另一个是true； 2. 这两个都是true)

在C语言中，位运算的或使用 单独的 |? ，判断条件的或使用两个 ||

位运算的或，一般用于求 两个位运算的集合的并集，

二、异或

异或XOR(Exclusive or)，Exclusive是专有的、独有的意思，也就是专门的一种或 or操作，与普通的or操作不同的是?XOR 主要用来判断两个值是否不同，和普通的或的差异在于 排除了 1 | 1 = 1这种情况。XOR按位不同则返回1，相同的返回0

或：?0 |? 1 = 1? 及? 1 | 1 =1

异或:? ? 1 |?0 =1? 及? 0 |?1 =1? ??

也就是说? 异或是 或的一个子集，异或将相同的1的这种情况排除了。

x ^ x = 0? ?自己与自己异或，肯定是0

x ^ 0 = x? ? 自己与0异或，还是自己，因为? 0 ^?0 = 0? ?0 ^?1=1 并没有变化。?

1、加密

text ^ key = cipherText

cipherText ^ key =? ?text ^ key ^ key = text ^ 0 = text

能用在AES的块加密上。

2、也可以用于求两个二进制字符串的汉明距离

从 000 -> 111

S = a ^ b? 能求出 从a到b需要变动的位，1代表差异需要变动的位，0代表相同无需变动。

然后求 |S| 这个二进制字符串有多少个1存在，就可以求出汉明距离。

如何求|S|的这个二进制字符串有多少个1 ？

可以通过 S-1 将最小位的1置0并且以及后面的0置1

S&(S-1) 将会 最小位的1置0，然后使用循环逐位置0，最后看S是否为0结束循环并返回1的个数。

可以使用下面的左移或右移或循环等，详细请看下面。

S&(S-1) = 0b+++++000

S^(S-1) = 0b+++++111

S&(-S) = lowbit(S)

3、交换x和y的值

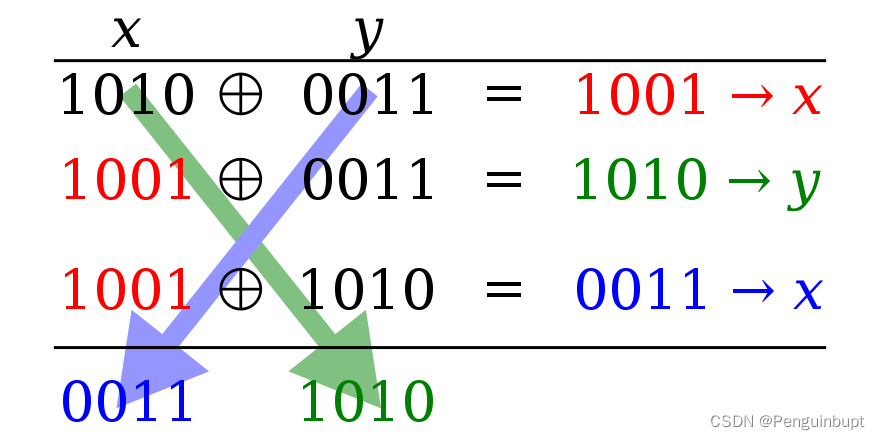
常规的交换是需要一个变量来存储临时的值，而通过异或交换算法，额外的存储是不需要的，算法如下所示：

X := X XOR Y; // XOR the values and store the result in X
Y := X XOR Y; // XOR the values and store the result in Y
X := X XOR Y; // XOR the values and store the result in X

通过三次异或操作来实现交换x和y的值。

4、按位取反

-1在n位的计算机中是 全1的一个串，这里以4位为例，因为负数在计算机中是以补码表示。

有符号数：?? 则将S进行取反，-1代表的是1111

无符号数：?，则将S进行取反

5、多个输入的数据，判断是否这些数据哪些位有奇数个1

最后结果是0b1100? 说明第0位和第1位是偶数个1，第2位和第3位是奇数个1

也可以用于奇偶校验位(parity bit)，进行错误检测，例如：串口通信中，会有一位是奇数偶数校验位

6、无进位的求和

下面的计算等效于将两个二进制的串进行不考虑进位的情况下的相加操作。

• 0b1110?XOR 0b1001?= 0b0111?(this is equivalent to addition without?carry)

三、应用

1. 案例

假设这个集合代表 学生是否签到，0代表未签到，1代表已签到，一个无符号的4位数字可以代表4个学生，两个集合代表两节不同的课程，那么

并集代表这4个学生中至少签到一节课的人

交集代表着4个学生两节课都签到的人

除 代表着 4个学生签到了第一节课，但是未签到第二节课。

S1:? 0101? ? ? ?S2: 0110

两个集合的并集：?? =? 0111? ? // 0号、1号、2号同学 至少签到了一节课

两个集合的交集：?? =? 0100? ?//? 2号同学 签到了两节课

两个集合的除：??=S1&(~S2)?= 0101 & 1001 = 0001? ?// 0号同学签到了第一节课，但是未签到第二节课。

2. 求一个字符串中有多少个1

方法1： 通过逻辑右移一位这个数字，同时使之和1进行与操作，直到为0。

方案2： 通过逻辑左移1，逐位与这个数字进行与操作，直到为0。

方案3： 通过 S&(S-1)将最右侧的1置0，这样逐次将最右边的1置0，直到为0。

public int bitCount(int n) {
    int count = 0;
    while (n != 0) {
        n &= n - 1;
        count++;
    }
    return count;
}

方案4： 通过查表，我们使用4位 0000-1111的数字进行存表，例如0000=0,1010=2，然后每次将数字逻辑右移4位来进行查表，得到1的总数。

方案5： 逐位相加，先是每一位相加，每两位相加，每四位相加，每八位相加等等。

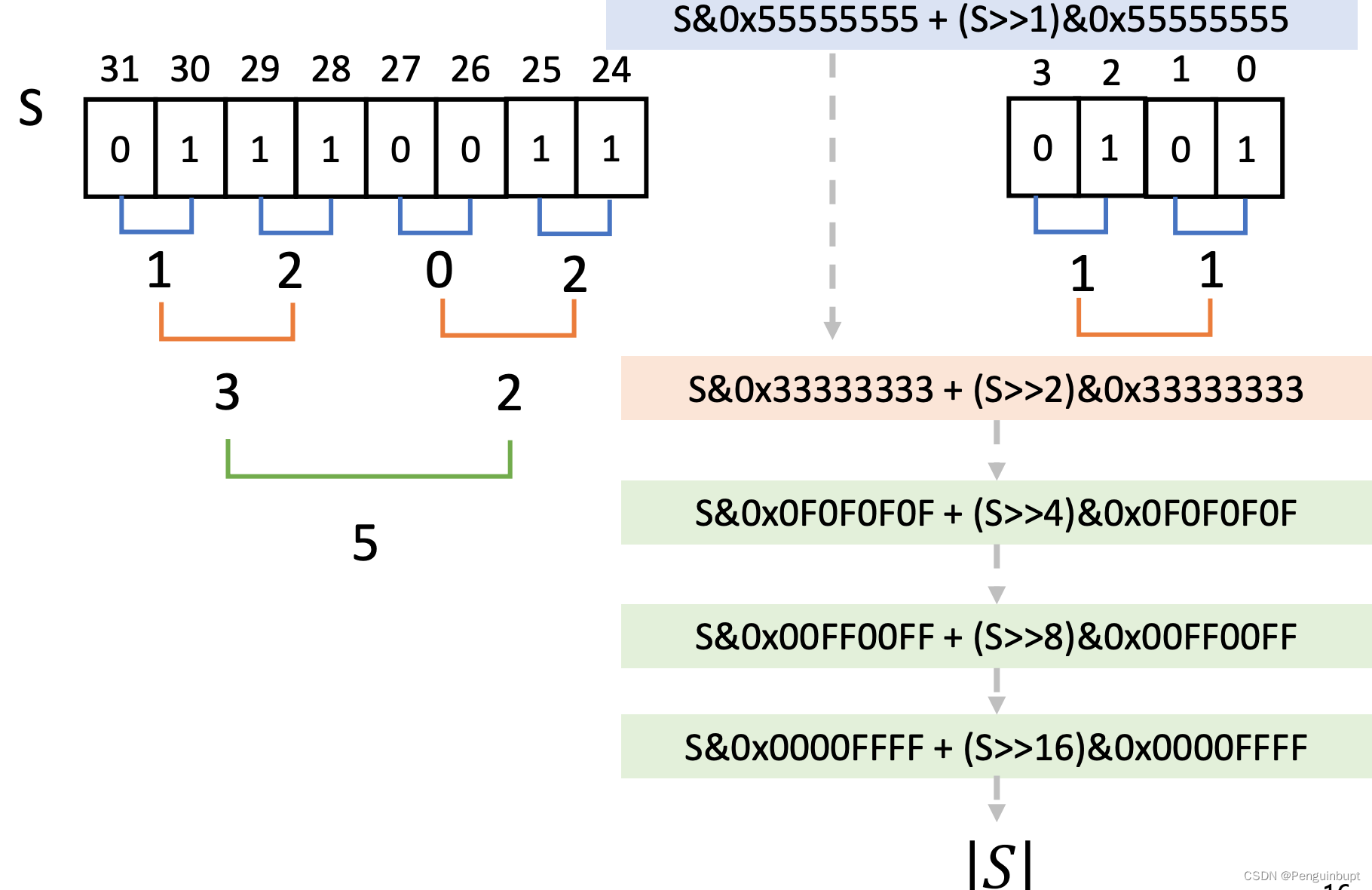
int bitset_size1(uint32_t S) { // SIMD
S = (S & 0x55555555) + ((S >> 1) & 0x55555555);
S = (S & 0x33333333) + ((S >> 2) & 0x33333333);
S = (S & 0x0F0F0F0F) + ((S >> 4) & 0x0F0F0F0F);
S = (S & 0x00FF00FF) + ((S >> 8) & 0x00FF00FF);
S = (S & 0x0000FFFF) + ((S >> 16) & 0x0000FFFF);
return S;
}

3. lowbit(x)

求x的最右侧的1的值

lowbit(x)= x & (-x)

假设x为一个有符号数的正数，那么-x则为负数，在计算机中以补码的方式存在。

x的源码为? ? 0010

(-x)原码为? ? 1010

(-x)反码为? ? 1101

(-x)补码为? ? 1110

取反加一，保证了最低位的1并没有变化，而左侧的其他位置均进行了变化。

发现将 x与(-x)进行与操作，可以得到最右侧的1的值。

x & (x-1) = 0b+++++000;

x ^ (x-1)? =?0b00000111;

x & (-x)? ?=? 0b00000100 (lowbit)

这个lowbit操作在 树状数组中有使用。

4. 求???

也就是求x的最左侧的1的位数

clz(Count Leading Zeros)用于求前导0的个数。

假设有32位数字， n = 32-clz(x) -1 为? 的值，即 00..0?.....

clz(x) + n + 1 = 32

int clz(uint32_t x) {
    int n = 0;
    if (x <= 0x0000ffff) n += 16, x <<= 16;
    if (x <= 0x00ffffff) n += 8, x <<= 8;
    if (x <= 0x0fffffff) n += 4, x <<= 4;
    if (x <= 0x3fffffff) n += 2, x <<= 2;
    if (x <= 0x7fffffff) n ++;
    return n;
}

参考文献：

0.Shift and rotate bits - Online Tools

1.?https://en.wikipedia.org/wiki/Bitwise_operation

2.?That XOR Trick

3.?https://en.wikipedia.org/wiki/Hamming_distance

4.https://en.wikipedia.org/wiki/XOR_swap_algorithm

5.bit manipulation - The difference between logical shift right, arithmetic shift right, and rotate right - Stack Overflow