机器学习——周志华

1.绪论

以很高的概率 得到一个很好的模型

1.1 机器学习过程

训练数据 (数据样本)

色泽	根	敲声	好瓜
青绿	蜷缩	沉浊	是
乌黑	蜷缩	沉浊	是
青绿	硬挺	沉浊	否
乌黑	蜷缩	清脆	否

经过训练(学习算法),得到

模型:决策树,神经网络,支持向量机,Boosting,贝叶斯网

1.2 基本术语

• 数据集:数据样本

  训练数据:用于得出模型

  测试数据:把模型拿来用

• 示例(instance):色泽 根 敲声

  样例(example):色泽 根 敲声 好瓜(结果)

• 属性(attribute):色泽 或者 根等

  属性空间:有几个属性就是几维属性空间(样本空间)

  特征向量(属性向量):属性空间中的向量(结果)

• 不可知样本(unseen data):未来的数据,不可知

• 假设:所用的模型,模型学到的东西,拟合函数f(x)

  真相:正确的答案y

• 分类:离散的输出 {yes,no},{big,middle,small}

  回归:连续的输出 [0,1]

• 监督学习(supervised learning):拿到的数据中有结果(知道好瓜标准是如何)

  无监督学习:拿到的数据中没有结果

• 独立同分布:只有样本满足独立同分布,他们之间才是无关的

  泛化:模型的泛用性 |f(x)-y|＜e (越小越好)

1.3 归纳偏好(Inductive Bias)

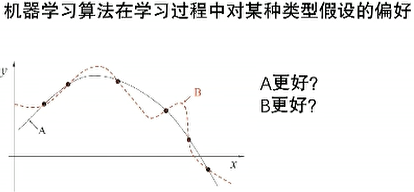
一般准则：奥卡姆剃刀(若非必要,勿增实体)

到底什么是更简单? ax^{2+bx+c还是ax}3+c ,进一步研究

学习算法的归纳偏好是否匹配问题决定了算法性能

1.4 NFL定理

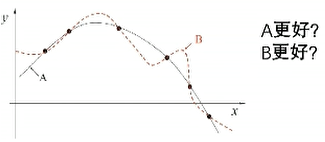
A和B谁更好?

黑点:训练样本 白点:测试样本

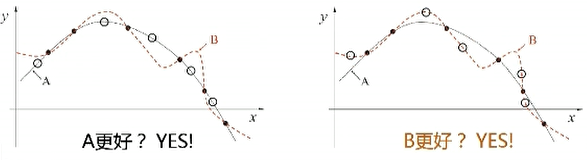
NFL定理(No Free Lunch没有免费午餐): 一个算法某些问题上A好,那比存在另一些问题B好

即脱离具体问题,谈论什么算法更好没有意义

具体问题,具体分析

2.模型评估与选择

2.1 泛化能力

什么模型好?

能很好适用于 unseen instance不可知样本

2.2 过拟合和欠拟合

泛化误差:在"未来"样本上的误差(越小越好)

经验误差:在训练集上的误差,即"训练误差"(可控)

经验误差是否越小越好? 经验误差越小可能出现"过拟合"

过拟合 VS 欠拟合

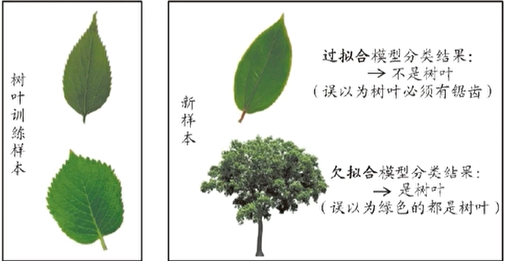
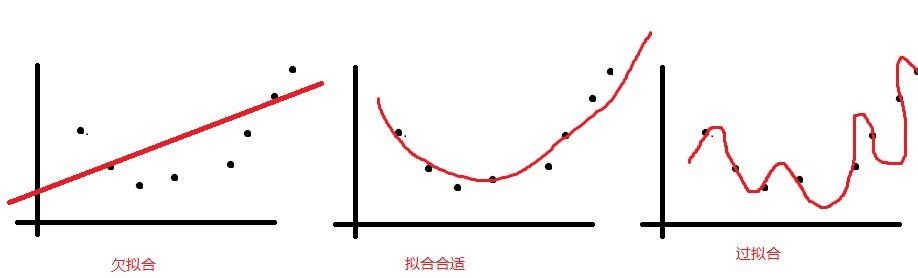
研究问题:这个算法是怎么解决Over Fitting的,这个办法什么时候会失效

2.3 三大问题

• 如何获得测试结果?

  没有unseen data的情况下用什么样的评估方法获得结果

• 如何评估性能优劣?

  性能度量,对于不同需求有不同的度量标准

• 如何判断实质差别?

  比较检验

2.4 评估方法

如何获得"测试集(test set)"

测试集应该与训练集"互斥",不可以从训练集中找几条数据进行测试

常见方法:

• 留出法(hold-out)

  将已有数据集留出一部分进行测试

  

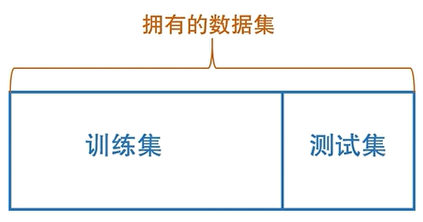
  注意

  • 保持数据分布一致性(eg:分层采样)

    不能训练集中的80个瓜都是好瓜,测试集中的20个全是坏瓜(所以要保持数据分布的一致性)

  • 多次重复划分(eg:多次随机取样)

  • 测试集不能太大,也不能太小

• 交叉验证(cross validation)

  解决留出法中随机取样取不到全部数据的尴尬情况

  • k-折(k-fold)交叉验证法

    

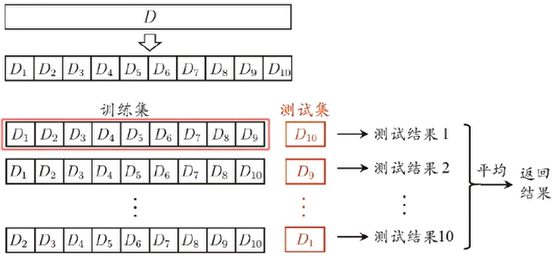
    上图为10折发,划分10个子集进行10次测试,每次取其中一个子集作为测试集,保证所有数据都会被用到

• 自助法(booststrap)

  上面两种方法对已有数据集M(100)进行评估时,总是要划分出m(k)作为测试集

  无法保证模型结果是100个数据的结果

  基于自助采样(有放回的采样,牺牲数据分布的一致性,换来数据量的一致性)

  

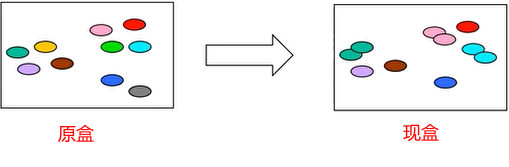
  原盒中取s个数据,将这s个数据复制一份放回原盒,然后取另外s个数据进行测试,这样就能在总数100不变的情况下,以牺牲数据分布一致性为代价换来数据个数的一致性

2.5 调参与验证集

• 算法的参数:人工设定,也称"超参数"(即人工对于模型的选择)

• 模型的参数:由学习确定

• 调参过程相似:先产生若干模型,然后基于某种评估方法进行选择

eg.利用多项式函数逼近数据
算法的参数:多项式的次数?由用户提供,是"超参数" ax^2+bx+c
模型的参数:确定上式abc

• 验证集(validation set)

  用于确定上述参数的选择

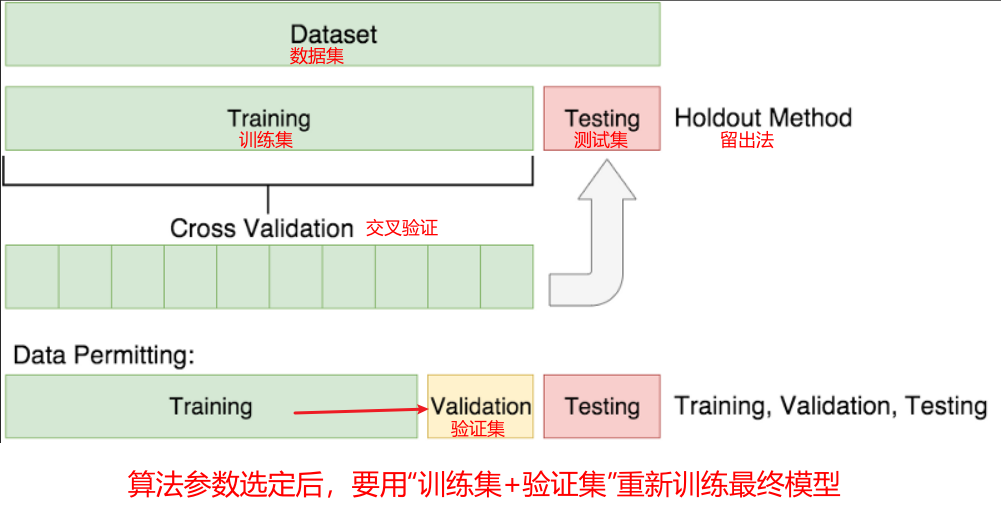
2.6 性能度量

什么样的模型是好的?

不仅取决于算法和数据,还取决于任务需求

• 回归(regression)任务常用的均方误差

  

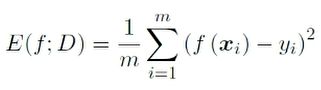
• 错误率

  

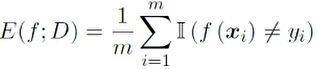
• 精度

  

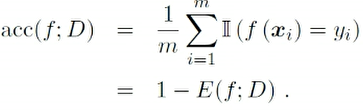
• 查准率

  

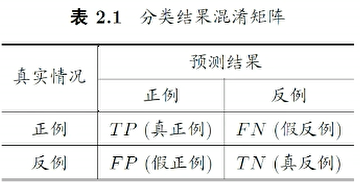
  TP:true positive

  FN:false negetive

  查准率:

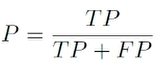
2.7 比较校验

在某种度量下取得评估结果后,是否可以直接比较评判优劣?

NO

• 测试性能不等于泛化性能

• 测试性能随着测试集的变化而变化

3.线性模型

通过属性的线性组合进行预测的函数

3.1 线性回归(Linear Regression)

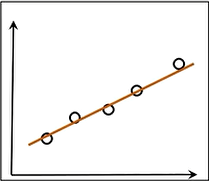
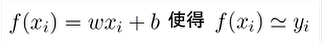
wi是属性,xi是权重

好瓜模型中:w1\*青绿色+w2*声音沉浊+w3\*根形态  显然是不合理的
对于属性这种离散的数据,要考虑期间是否存在'序'的关系

即考虑离散数据连续化

• 如果有序:(高 中 低)->1,0.5,0
• 如果无序:(蓝 绿 白)->(100),(010),(001) k维属性变成k维向量

3.2 最小二乘解

线性回归问题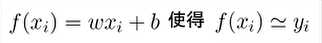目的就是求w向量和b求最似函数,相似度量可以采用均方计算

求最小值: 对w,b偏导,令偏导数为0 ,得到似然函数最小值时的解(w,b)

多元函数无条件极值必要条件: 令x,y偏导=0

线性回归问题中,对似然函数求导的极值点一定是极小值点

3.3 多元线性回归

线性回归问题中,xi是i个值

多元线性回归中,xi是向量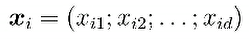比如x11为敲声,x12为根形态,x13为色泽

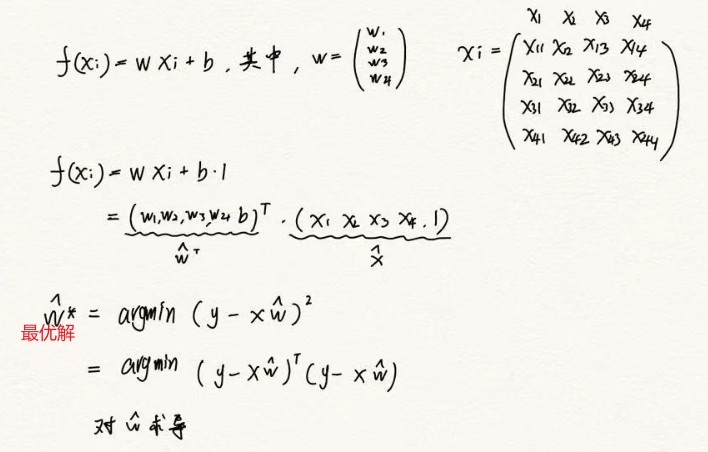
**求解:**x解向量的求解可以采用矩阵方程

• 

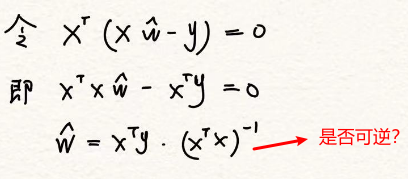
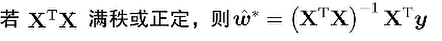
  r(A)=r(A|b)=n,唯一解

• 

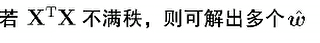
  r(A)=r(A|b)<n,无穷解

  求出无穷解w如何选用最好的w拟合模型呢?

  归纳偏好

  对于解出多个w,也就是多个对应模型,那么用哪个更好,这就是归纳偏好所研究的内容

  

  方法:正则化
  对于求出的多个模型
  a*x^2+b*x+c和
  c*x^3+d*x^2+e*x+f
  加入一个限制如:要求最高次最小or要求x系数最小等
  

3.4 广义线性模型

3.5 对率回归

3.6 对率回归求解

3.7 线性判别分析

3.8 类别不平衡

4.决策树

4.1 决策树基本流程

4.2 信息增益划分

4.3 其他属性划分准则

4.4 决策树的剪枝

4.5 预剪枝与后剪枝

4.6 缺失值的处理

5.支持向量机

5.1 支持向量机基本型

5.2 对偶问题与解的特性

5.3 求解方法

5.4 特征空间映射

5.5 核函数

5.6 软间隔SVM

5.7 正则化

5.8 如何使用SVM?

6.神经网络

6.1 神经网络模型

6.2 万有逼近能力

6.3 BP算法推导

6.4 缓解过拟合

7.贝叶斯分类器

7.1 贝叶斯决策论

7.2 生成式和判别式模型

7.3 贝叶斯分类器与贝叶斯学习

7.4 极大似然估计

7.5 朴素贝叶斯分类器

7.6 拉普拉斯修正

8.集成学习和聚类

8.1 集成学习

8.1 好而不同

8.1 两类常用集成学习方法

8.1 Boosting

8.1 Bagging

8.1 多样性度量

8.1 聚类

8.1 距离计算

8.1 聚类方法概述