【算法笔记】状态机dp
发布时间:2024年01月07日
状态机dp概述
当一个事件涉及的过程的考虑并且方案数的考虑比较繁琐时,我们可以尝试用状态机的思想去考虑这个问题,将这个问题简化,就是去考虑一个对象他所具有的几种状态。
状态机主要考虑一下两个方面:状态和转移
状态其实也就是正常在dp过程中分析的,不用过多解释了。
转移:状态与状态之间的转移,根据实际题目,分析状态与状态之间是否能转移,能转移的就画一根箭头。最后会发现其实就是一个有向图。
触发机制
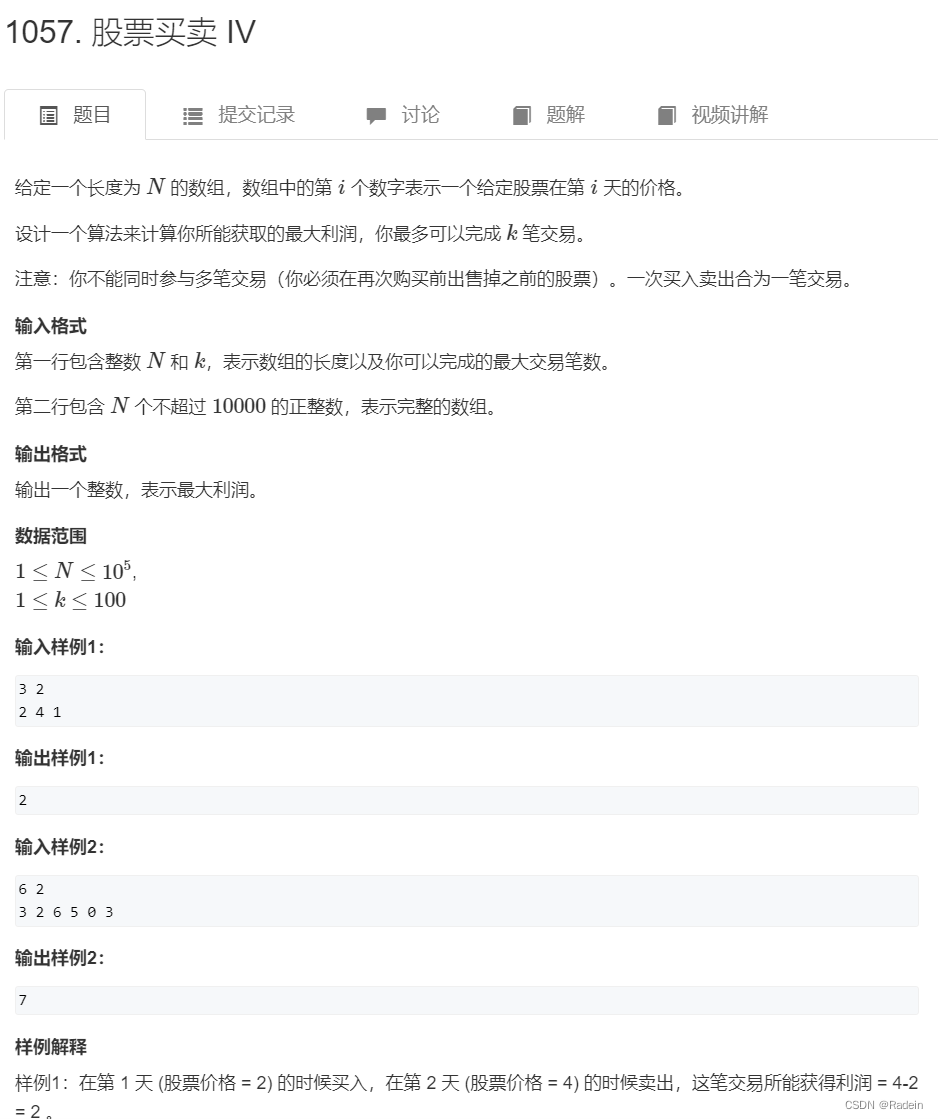
样题:股票买卖IV
?
状态含义:f[i, j, 0]表示前i个股票,已经进行完j次交易,且手中没有买入时的最大收益;
?f[i, j, 1]表示前i个股票,已经进行完 j - 1次交易,且已经买入第j个股票但还没卖出时的最大收益。
关于初始化:因为在最开始,我们任何一笔交易都没有产生,并且手中也没有任何股票,也就不能个进行卖出的操作。所以我们第一次操作就是从0变到1(买入股票)或继续保持0(不买股票)。所以我们直接将f[ i ][ 0 ][ 0 ]初始化为0。这样就完成了每个数据点的初始化,避免了不合法的方案进行转换。
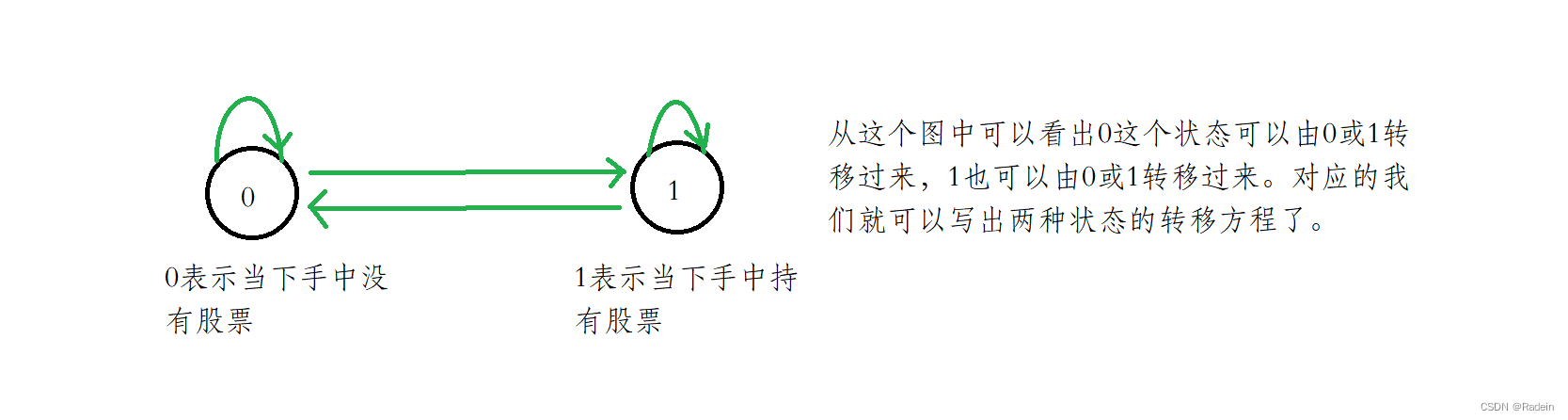

? ? ? ? ?
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100010, M = 110;
int f[N][M][2];
int n, k;
int w[N];
int main()
{
cin>>n>>k;
for(int i = 1; i <=n; i ++) cin>>w[i];
memset(f, -0x3f, sizeof f);
for(int i = 0; i <= n; i ++) f[i][0][0] = 0;
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= k; j ++)
{
f[i][j][0] = max(f[i-1][j][1] + w[i], f[i - 1][j][0]);
f[i][j][1] = max(f[i - 1][j][1], f[i-1][j-1][0] - w[i]);
}
}
int res = 0;
for(int i = 0; i <= k; i ++)
{
res = max(res, f[n][i][0]);
}
cout<<res;
}样题2:股票买卖V
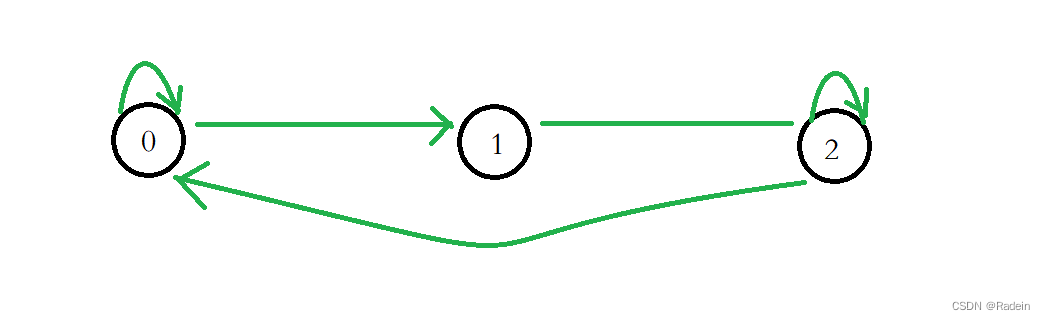
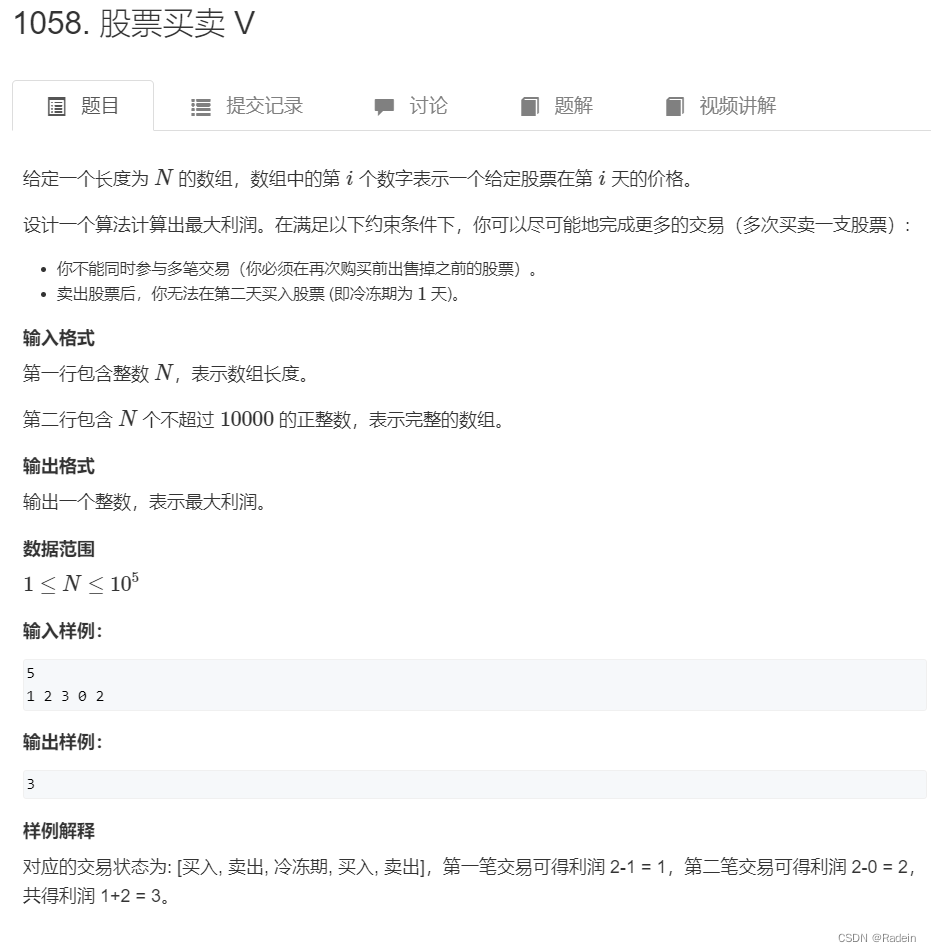 思考:这题和上面那题最大不同就是,这里可以进行无限多次交易,同时多了一个状态。这一题中共有三个状态:手中持有股票,刚刚卖出股票那一天,卖出股票天数大于等于2天。
思考:这题和上面那题最大不同就是,这里可以进行无限多次交易,同时多了一个状态。这一题中共有三个状态:手中持有股票,刚刚卖出股票那一天,卖出股票天数大于等于2天。
状态转移的分析过程就和上一题思路类似。照着图把转移方程写出来。
?
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100010;
int f[N][3];
int n;
int w[N];
int main()
{
cin>>n;
for(int i = 1; i <= n; i ++) cin>>w[i];
memset(f, -0x3f, sizeof f);
f[0][2] = 0;
for(int i = 1; i <= n; i ++)
{
f[i][0] = max(f[i-1][0], f[i - 1][2] - w[i]);
f[i][1] = f[i-1][0] + w[i];
f[i][2] = max(f[i-1][1], f[i-1][2]);
}
cout<<max(f[n][1],f[n][2]);
}
文章来源:https://blog.csdn.net/Radein/article/details/135420120
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 如何用CHAT绘制扇形图代码?
- redis—List列表
- docker查看日志
- 全国消费水平展示平台(JSP+java+springmvc+mysql+MyBatis)
- Python Process创建进程(2种方法)详解
- 在线课堂预约小程序源码系统 附带完整的搭建教程
- office三剑客从基础到精通,Word+Excel+PPT从新手到高手
- 二手买卖、废品回收小程序 在app.json中声明permission scope.userLocation字段 教程说明
- PromptNER: Prompt Locating and Typing for Named Entity Recognition
- Python处理音频