遗传算法（内附代码）

一.研究背景:

遗传算法是从生物现象遗传规律总结而出的。它是根据种群的不断衍化，个体间作为父本和母本产生新的个体，在这一过程中，基因进行交叉、变异、选择。通过不断的衍化逐渐使种群朝向整体逐渐优化（整体基因逐渐得到改良的过程）。这和严复的天演论中“物竞天择，适者生存”相一致，同时也相符与达尔文的物种进化适者生存的原理。但是对于遗传算法贡献最大的生物学理论还应该属孟德尔的豌豆杂交试验，从其中来的染色体交叉、基因变异等理论，这对于遗传算法给出了直接的启示。

1975年美国的Michigan大学J.Holland教授首先提出来这种通过模拟自然进化过程搜索最优解的方法。

二．研究目的及意义:

建立香蕉褐变面积比（x）与香蕉褐变区域生化指标酶活（y）的样本参数构建两者的回归方程并优化回归方程的参数，能够使用回归方程相互计算出对应的值，避免大量重复的实验，提高效率。

三．研究内容

要求根据给出的香蕉褐变面积比（x）与香蕉褐变区域生化指标酶活（y）的样本参数构建两者的回归方程，使用遗传算法对回归方程参数进行优化。

（1） 可建立一元线性回归方程

（2） 说明遗传算法中的评价函数。

（3） 说明遗传算法中参数的取值。

（4） 给出结果分析。

（5） 附录中提供程序等材料。

四、方法步骤

1、建立一元一次回归方程

根据给出的香蕉褐变面积比（x）与香蕉褐变区域生化指标酶活（y）的样本参数，在matlab中调用数据曲线拟合工具箱，进行数据曲线拟合，拟合结果如下：

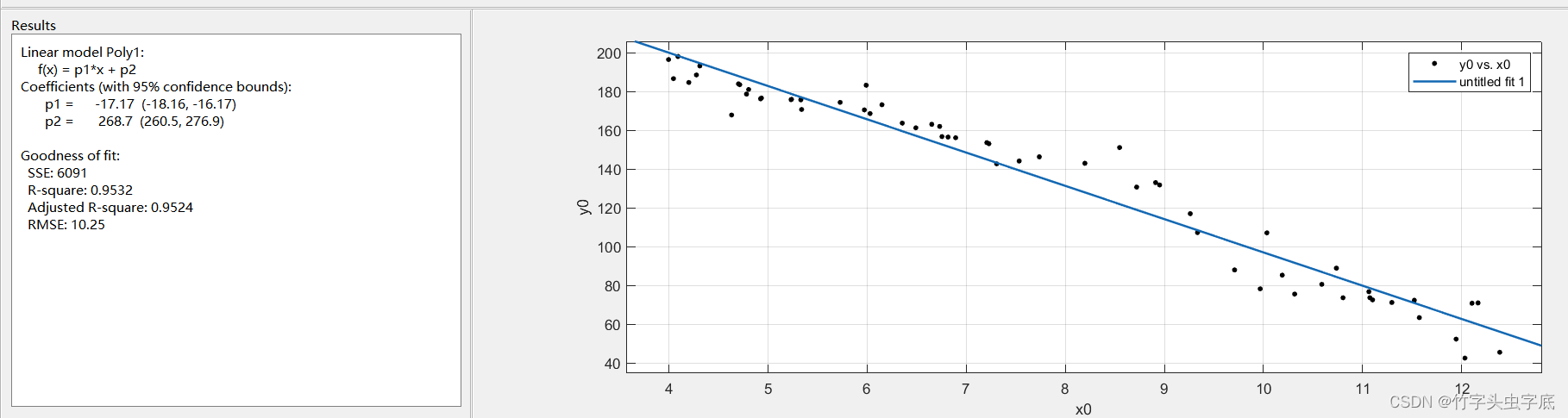
一元一次回归方程：y=-17.17x+268.7

1. 根据回归方程建立目标函数：F=a.*x0+b；（注：a为斜率，x0为香蕉褐变面积比样本参数，b为常数）

3、根据要求建立评价函数：P=abs(F-y0);（注：y0香蕉褐变区域生化指标酶活为样本参数，F为目标函数计算的香蕉褐变区域生化指标酶活，P为F和y0之间的绝对误差值）

4、设定基本遗传算法的运行参数

种群Size：60 ?????复制概率Pc=0.6

迭代次数G：300 ????变异概率Pm=0.1

精度CodeL=10

• 五、结果及分析

1、算法结果如下图：

2、优化参数结果如下图：

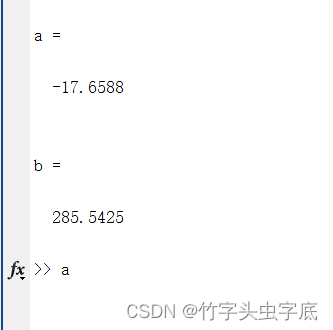
3.结果分析：

遗传算法在100代之前完成收敛，遗传算法优化的一元线性回归方程参数和使用数据拟合工具箱的结果相差不大，说明本次遗传算法优化结果较为理想，多次运行程序，选择优化最好的优化结果结果。

建立一元线性回归方程：y=-17.6588x+285.5425

六、程序附录：

clc;clear all; close all;

Z=xlsread('C:\Users\liukongyuan\Desktop\b.xls','sheet1');

x0=Z(:,1);

y0=Z(:,2);

%Parameters

Size=60;

G=300;

CodeL=10;

umax=-15;

umin=-20;

imax=290;

imin=260;

E=round(rand(Size,2*CodeL)); %Initial Code

%Main Program

for?k=1:1:G

time(k)=k;

for?s=1:1:Size

m=E(s,:);

y1=0;y2=0;

%Uncoding

m1=m(1:1:CodeL);

for?i=1:1:CodeL

y1=y1+m1(i)*2^(i-1);

end

a=(umax-umin)*y1/1023+umin;

m2=m(CodeL+1:1:2*CodeL);

for?i=1:1:CodeL

y2=y2+m2(i)*2^(i-1);

end

b=(imax-imin)*y2/1023+imin;

F=(a.*x0+b);

P=abs(F-y0);

end

Ji=P;

BestJ(k)=min(Ji);

fi=1./P;

%*****

[Oderfi,Indexfi]=sort(fi);

fi_sum=sum(fi);

fi_Size=(Oderfi/fi_sum)*Size;

fi_S=floor(fi_Size); %Selecting Bigger fi value

kk=1;

for?i=1:1:Size

for?j=1:1:fi_S(i) %Select and Reproduce fi_S(i)

TempE(kk,:)=E(Indexfi(i),:);

kk=kk+1; %kk is used to reproduce

end

end

%*****

pc=0.60;

n=ceil(20*rand);

for?i=1:2:(Size-1)

temp=rand;

if?temp<pc %Crossover Condition

for?j=n:1:20

TempE(i,j)=E(i+1,j);

TempE(i+1,j)=E(i,j);

end

end

end

TempE(Size,:)=E(Indexfi(Size),:);

E=TempE;

%********

pm=0.1; %Big mutation

for?i=1:1:Size

for?j=1:1:2*CodeL

temp=rand;

if?temp<pm %Mutation Condition

if?TempE(i,j)==0

TempE(i,j)=1;

else

TempE(i,j)=0;

end

end

end

end

TempE(Size,:)=E(Indexfi(Size),:);

E=TempE;

end

a

b

figure(1);

plot(time,BestJ);

xlabel('Times');ylabel('误差');