【算法】Java-二叉树的右视图(BFS、DFS两种解法)

题目要求：

给定一个二叉树的?根节点?root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

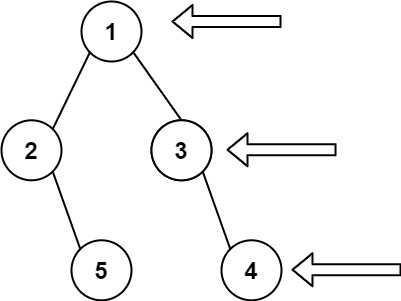
输入:?[1,2,3,null,5,null,4]
输出:?[1,3,4]

示例 2:

输入:?[1,null,3]
输出:?[1,3]

示例 3:

输入:?[]
输出:?[]

提示:

二叉树的节点个数的范围是[0,100]
-100<= Node.val <= 100

---

题目分析：

右视图，不仅仅是返回右子树上的节点，如果是一颗这样的树，我们要返回：1 ?3 5。

如果只返回右子树的节点，只返回1 3，就不符合右视图了。

返回每个层次最后一个节点，所以我用的第一个方法是：BFS-广度优先遍历。

方法一：广度优先遍历

思路：遍历每一层，将下一层的节点存到队列；如果是最后一个节点，add到返回集合；

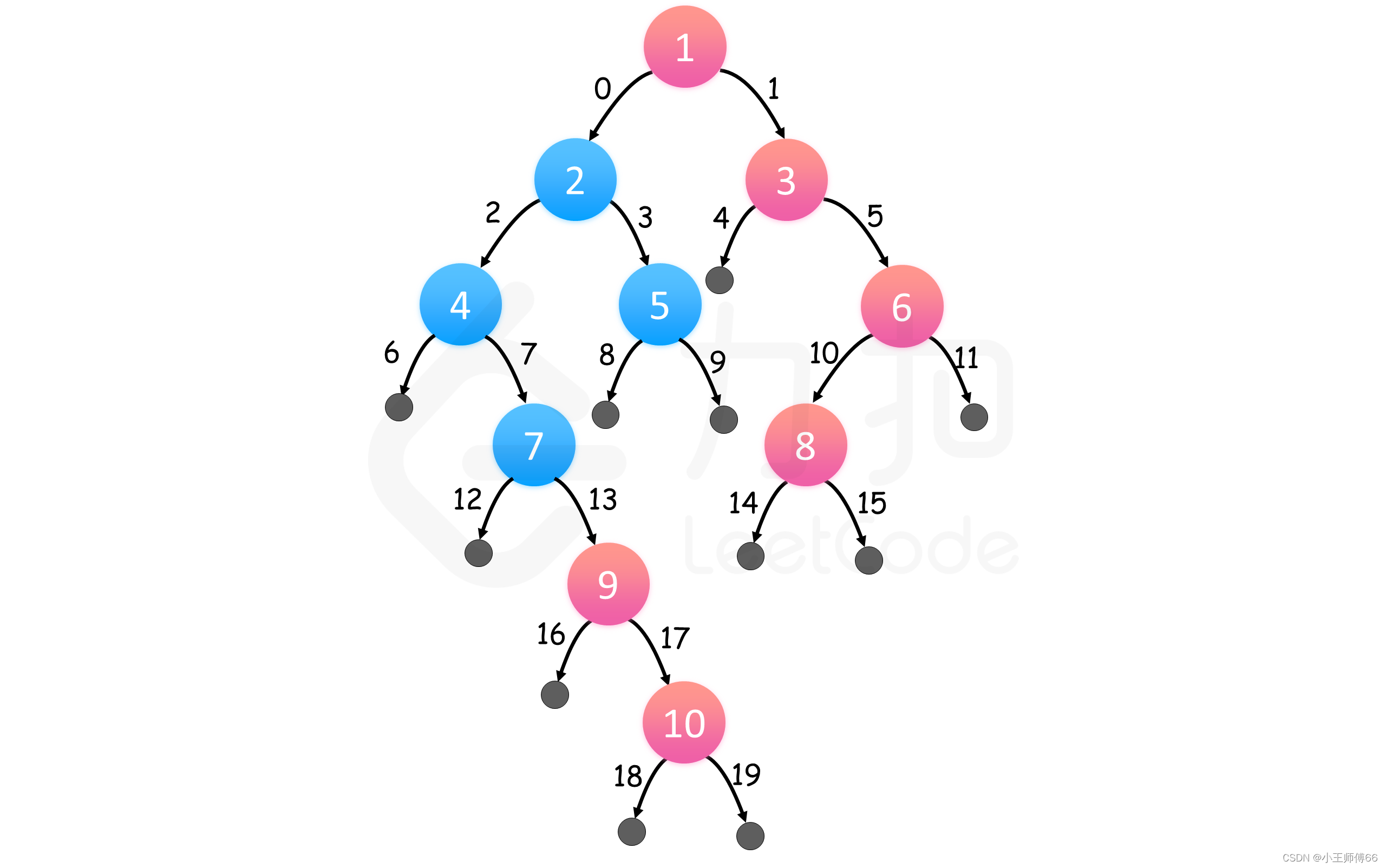
public class RightViewTree {
	
	public List<Integer> rightSideView(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }

        ArrayDeque queue = new ArrayDeque(); 
        queue.offer(root);
        while (queue.size() > 0) {
            int count = queue.size(); // ①记录当前层有多少个节点
            for (int i = 0; i < count; i++) {
                TreeNode node = (TreeNode) queue.poll();
                if (node.getLeftNode() != null) {
                    queue.offer(node.getLeftNode());
                }
                if (node.getRightNode() != null) {
                    queue.offer(node.getRightNode());
                }
                // 遍历到最后一个 add 到res
                if (i == count - 1) {
                    res.add(node.val);
                }
            }
        }
        return res;
    }
}

另外：这是最终版，前面几版，除了把问题理解成了输出右子树的节点，还这样写过：

public List<Integer> rightSideView(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        ArrayDeque queue = new ArrayDeque();
        queue.offer(root);
        int count = 1; // ①记录每层的节点个数
        while (queue.size()> 0){
            int add = 0;
            // 遍历队列 拿最后一个
            for(int i = 0; i < count ; i ++){
                TreeNode node =(TreeNode) queue.poll();
                if(node.getLeftNode() != null){
                    queue.offer(node.getLeftNode());
                    add ++;
                }
                if(node.getRightNode() != null){
                    queue.offer(node.getRightNode());
                    add ++;
                }
                // 遍历到最后一个 add 到res
                if(i == count -1){
                    res.add(node.val);
                }
            }
            count = add;
        }
        return res;
    }

时间复杂度:O(N);

空间复杂度:O(N);

①与最终版的区别在于，如何记录每层的节点数，这里用了一个临时变量count；

学习了其他博主的写法之后，意识到每次for循环结束后，add到queue中的节点，就是下一层所有节点了，不用单独记，直接取size可以。

（后来我想当时还是没把queue中存的内容想清楚，才又count了一下，所以在这里标识一下）

方法二：深度优先遍历

思路：按照根->右->左 遍历二叉树，保证每层都是最先访问最右边的节点。

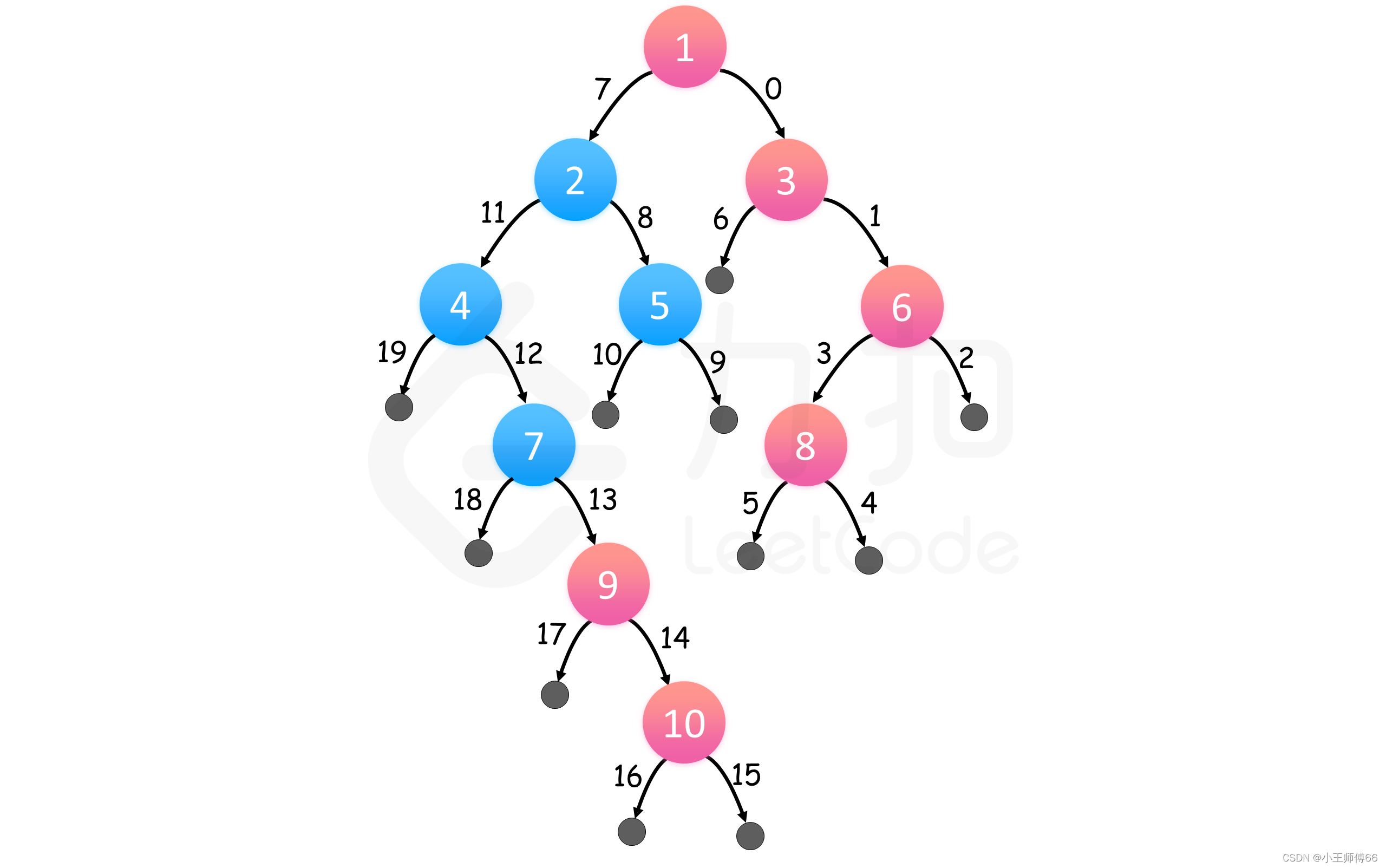
? ? ? 这个方法最开始我没想出来，后来看了别人的解题思路，理解到这种方法的关键在于：遍历每个节点时，如何知道这个深度是否已经记录过最右侧的节点了？大家看答案之前可以先想一想。

答：使用递归，将深度作为入参记录到栈帧。

将节点add到返回集合中；通过对比深度和集合中节点的数量，就知道该层是否已经记录过。

public class RightViewTree {


    private static List<Integer> res = new ArrayList<>();



    /**
     * 深度优先遍历
     * @param root
     * @return
     */
    private List<Integer> rightSideView(TreeNode root) {
        dfs(root, 0); // 从根节点开始访问，depth=0
        return res;
    }

  
    // 在使用递归进行深度优先遍历时，每个栈帧保存当时的depth。
    private void dfs(TreeNode root, int depth) {
        if (root == null) {
            return;
        }
        // 先访问 当前节点，再递归地访问右子树、左子树。
        // 每一层的depth一定，当depth>=res.size()时，说明该层还未记录，将节点add到返回集合中；在本题中，不会出现大于的情况，所以只需判断等于。
        // 又因为我们遍历的顺序是根-右-左，所以root一定是当前深度最右边的节点。
        if (depth == res.size()) {  
            res.add(root.val);
        }
        depth++; // 准备记录下一层
        dfs(root.getRightNode(), depth);
        dfs(root.getLeftNode(), depth);
    }


}

时间复杂度：O(N);

空间复杂度:O(N);

? ? 对于深度优先遍历或递归不了解的朋友，可能对depth的变化不太理解。可以结合栈帧中记录，多debug几遍。

? ? 方法二可以帮助我们更好的理解递归中，递和归的过程，以及过程中变量的变化。

写在最后：

? ? ? 这道题的解法有很多，分享这两种解法的原因是在做这道题时，我感受到了自己的一点点质变。方法一，对队列的熟练应用。方法二，深度理解了递归的过程，后面还要继续应用，继续体会。

? ? ? 学习算法增加了我看问题的视角，经常感叹“原来可以这样”，“居然还能这样”，“这人想的真好”之类。但我们知道“知道”和“做到”之间，有一条“鸿沟”，用新的“知道”的方法解出题的感觉真是太棒了，我做到了！当然，过程非常不容易，经常有些题目都看不懂，或者别人的思路理解不了。这时候，我们要想想，这道题难度是不是太大了，如果太大，要降低难度；否则，多debug，或者把步骤一步步写在纸上，是个不错的方法；或者多看看别人的解题思路。

? ? ?开年的第一篇博客，是关于对算法的思考，太不可思议了！小王师傅做到了！希望能帮到一些朋友，有更多的朋友做到！

参考：

LeetCode官方：. - 力扣（LeetCode）

LeetCode?Sweetiee博主的分享：. - 力扣（LeetCode）