CCF模拟题 202212-2 训练计划
CCF_2022-12-2
试题编号: 202212-2
试题名称: 训练计划
时间限制: 1.0s
内存限制: 512.0MB
训练计划
问题背景
西西艾弗岛荒野求生大赛还有 n 天开幕!
问题描述
为了在大赛中取得好成绩,顿顿准备在 n 天时间内完成“短跑”、“高中物理”以及“核裂变技术”等总共 m 项科目的加强训练。其中第 i 项(1<=i<=m)科目编号为 i,也可简称为科目 i。已知科目 i 耗时 ti 天,即如果从第 a 天开始训练科目 i,那么第 a+ti-1 天就是该项训练的最后一天。
大部分科目的训练可以同时进行,即顿顿在同一天内可以同时进行多项科目的训练,但部分科目之间也存在着依赖关系。如果科目 i 依赖科目 j,那么只能在后者训练结束后,科目 i 才能开始训练。具体来说,如果科目 j 从第 a 天训练到第 a+tj-1天,那么科目 i 最早只能从第 a+tj 天开始训练。还好,顿顿需要训练的 m 项科目依赖关系并不复杂,每项科目最多只依赖一项别的科目,且满足依赖科目的编号小于自己。那些没有任何依赖的科目,则可以从第 1 天就开始训练。
对于每一项科目,试计算:
1)最早开始时间:该科目最早可以于哪一天开始训练?
2)最晚开始时间:在不耽误参赛的前提下(n 天内完成所有训练),该科目最晚可以从哪一天开始训练?
n天内完成所有训练,即每一项科目训练的最后一天都要满足 <=n。需要注意,顿顿如果不能在 n 天内完成全部 m 项科目的训练,就无法参加大赛。这种情况下也就不需要再计算“最晚开始时间”了。
输入格式:
从标准输入读入数据
输入共三行
输入的第一行包含空格分隔的两个正整数 n 和 m,分别表示距离大赛开幕的天数和训练科目的数量。
输入的第二行包含空格分隔的 m 个整数,其中第 i 个(1<=i<=m)整数 pi 表示科目 i 依赖的科目编号,满足0<=pi<i;pi=0 表示科目 i 无依赖。
输入的第三行包含空格分隔的 m 个正整数,其中第 i 个(1<=i<=m)数 ti 表示训练科目 i 所需天数,满足1<=i<=n。
输出格式:
输出到标准输出中
输出共一行或两行
输出的第一行包含空格分隔的 m 个正整数,依次表示每项科目的最早开始时间。
如果顿顿可以在 n 天内完成全部 m 项科目的训练,则继续输出第二行,否则输出到此为止。
输出的第二行包含空格分隔的 m 个正整数,依次表示每项科目的最晚开始时间。
样例 1 输入
10 5
0 0 0 0 0
1 2 3 2 10
样例 1 输出
1 1 1 1 1
10 9 8 9 1
样例 1的说明:
五项科目间没有依赖关系,都可以从第 1 天就开始训练。
10 天时间恰好可以完成所有科目的训练。其中科目 1 耗时仅 1 天,所以最晚可以拖延到第 10 天再开始训练;而科目 5 耗时 10 天,必须从第 1 天就开始训练。
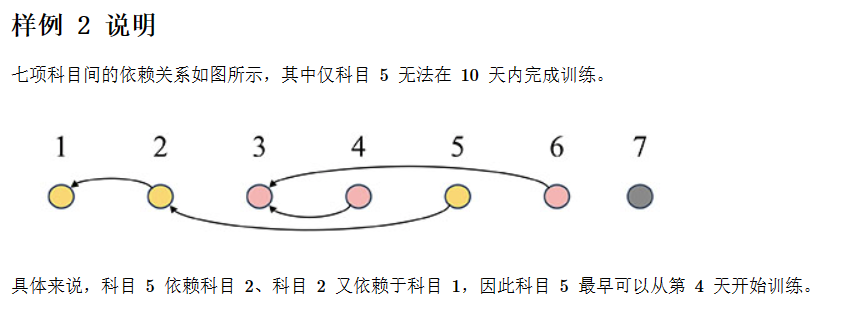
样例 2 输入
10 7
0 1 0 3 2 3 0
2 1 6 3 10 4 3
样例 2 输出
1 3 1 7 4 7 1
样例 3 输入
10 5
0 1 2 3 4
10 10 10 10 10
样例 3 输出
1 11 21 31 41
子任务
70%的测试数据满足:顿顿无法在 n 天内完成全部 m 项科目的训练,此时仅需输出一行“最早开始时间”;
全部的测试数据满足 0<n<=365 且 0<m<=100。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 轻松监测空气质量:了解空气质量查询API的功能
- springboot集成swagger
- 全网最全Midjourney以图生图的详细教程 内有6种案例 小白必收藏!!!!
- 软件需求分析(大学图书馆管理系统之大学图书馆数字化转型)
- 判断自守数
- 普中STM32-PZ6806L开发板(HAL库函数实现-访问多个温度传感器DS18B20)
- SpringBoot常见请求参数
- aram 流水灯
- [Django-05 ]自定义sql查询
- XML简介 (EXtensible Markup Language)