【ICCV 2023】MPI-Flow：什么，只需要单张图片就能训练光流估计模型了？

来源：ICCV 2023
机构：北京理工大学 & 小红书
论文题目：MPI-Flow: Learning Realistic Optical Flow with Multiplane Images

本文的关键思路在于将单图→多视角生成模型，引入数据合成思路，用于多视角任务的训练

论文链接：https://arxiv.org/abs/2309.06714

原版开源代码（生成本地数据）：https://github.com/Sharpiless/MPI-Flow

新版开源代码（在 Dataloader 中）：https://github.com/Sharpiless/Train-RAFT-from-single-view-images

12.18 作者更新了 Online-training 版本代码，当前只需要准备应用场景的单视角图像，就可以无缝衔接光流估计模型的训练代码（例如 RAFT），并且增强的合成数据的随机性。

引言：

基于学习的光流估计模型的准确性在很大程度上依赖于训练数据集的真实性。目前，生成这类数据集的方法要么使用合成数据，要么以有限的真实性生成图像。然而，这些数据与真实世界场景的领域差距，限制了训练模型的泛化到真实世界的应用。

主要贡献：

为了解决这个问题，本文研究从真实世界的图像中生成真实的光流数据集：

• 首先，为了生成高度逼真的新图像，本文从单视图图像中构建了一个分层深度表示法，称为多平面图像（MPI）。这使得我们能够生成高度逼真的新视角图像。为了生成与新图像准确对应的光流图，本文使用相机矩阵和平面深度来计算每个平面的光流。然后，本文将这些分层的光流投影到具有体积渲染的输出光流图中。
• 其次，为了保证运动的真实性，本文提出了一个独立的物体运动模块，可以在MPI中分离摄像机和动态物体运动。该模块解决了基于mpi的单视图方法的缺陷，其中光流仅由摄像机的运动产生，而不考虑任何物体的运动。
• 此外，本文还设计了一个深度感知的内部绘制模块来合并新的图像与动态对象，并解决非自然的运动遮挡。

通过在真实数据集上的大量实验，本文展示了提出的方法的优越性能。此外，提出的方法在基于学习的模型的无监督和监督训练中都取得了最先进的性能。

Motivation：

近年来，随着神经网络的快速发展，与传统的基于模型的算法相比，基于学习的算法取得了重大进展。传统的实践主要依赖于合成数据，其中，合成数据包含精确的光流标签和动画图像。然而，合成数据和真实数据之间的领域差距阻碍了它在现实应用中的进一步改进。

最近的研究旨在是利用手工制作的特殊硬件，从真实数据中提取光流。然而，严格控制和低效的收集程序限制了它们的适用性。为了解决这个问题，Depthstillation [1] 和 RealFlow [12] 被提出，利用随机运动将真实图像中的每个像素投影到新的视图帧上，并通过虚拟摄像机合成光流。尽管如此，这两种方法都受到了缺乏图像真实性的限制，导致了诸如碰撞、孔洞和伪影等问题。这些限制限制了基于学习的光流模型的实际性能。

为了实现更高的图像真实感，本文将注意力转向使用单视图多平面图像（MPI）。这系列工作展示了显著的单视图图像渲染能力，并有效地减少了以前方法中常见的碰撞、孔和伪影。这些进步有助于提高更高的图像真实感，引发了一个自然的问题：高真实度的MPI方法能否用于生成用于训练目的的高质量光流数据集？

为此，本文提出了MPI-Flow，旨在从真实世界的图像中生成具有真实感的光流数据集。具体来说，本文首先回顾了 MPI 的图像合成管道，并设计了一个伴随图像合成的光流生成管道：MPI-Flow。在这一步中，本文通过将预测的颜色和密度扭曲到每个分层平面上来构建一个 MPI。然后，颜色和密度被映射到一个真实的新图像通过体积渲染。利用分层平面，本文从渲染图像和真实图像中提取具有虚拟摄像机运动的光流。

其次，由于MPI只能应用于静态场景，产生有限的运动真实性，本文提出了一个独立的物体运动模块和一个深度感知绘画模块来解决这个问题。独立对象运动模块将动态对象与静态场景解耦，并应用不同的虚拟摄像机矩阵来计算动态和静态部分的运动。最后引入一种深度感知的图像修复模块，来消除合成新图像中的对象遮挡。

算法细节：

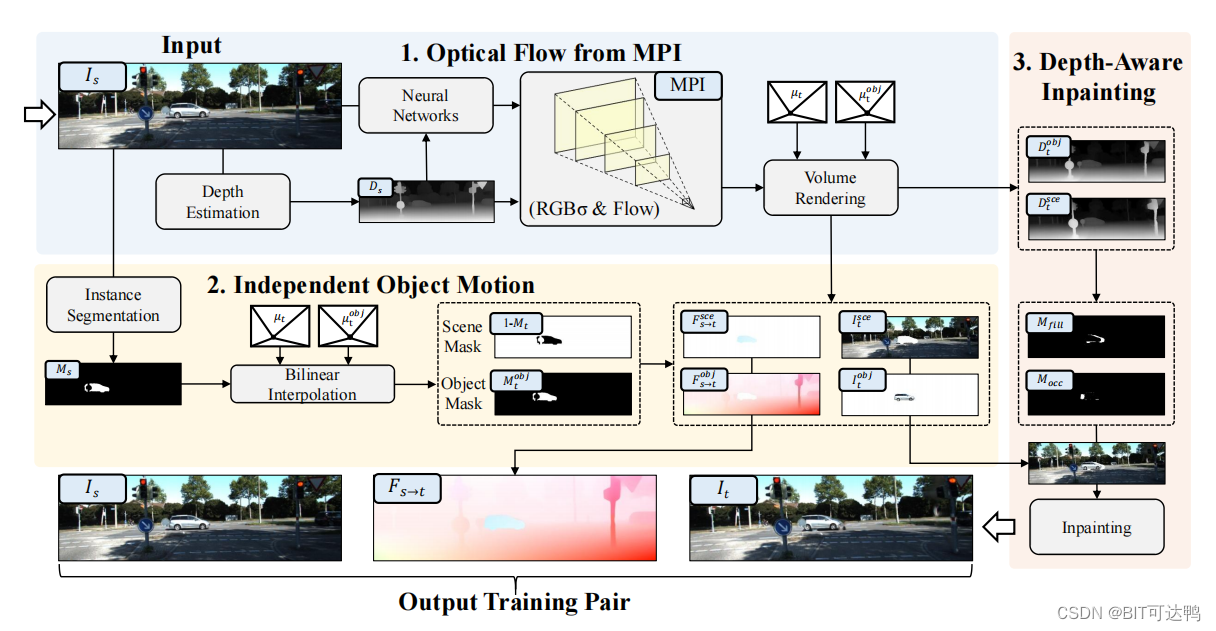
本文提出的 MPI-Flow 框架采用单视图图像作为输入，并通过估计深度来构建MPI，其中每个平面的RGB和密度由神经网络预测，每个平面的光流由摄像机矩阵计算。新视图和光流图都是通过体渲染来渲染的，并由带有新视图对象掩模的独立对象运动模块来分隔。新图像通过深度感知的图像合并。

Optical Flow Data Generation

为了在目标新视角下渲染真实的图像，我们以可区分的方式从原视角的 MPI 进行像素扭曲。具体来说，我们使用神经网络预测在源视角下使用颜色通道、密度通道和深度（${\mathbf{c}}_n,{\mathbf{\sigma }}_n,{\mathbf{d}}_n$）：

{ ( c n , σ n , d n ) } n = 1 N = F ( I s , D s ) \left\{\left(\mathbf{c}_n, \boldsymbol{\sigma}_n, \mathbf{d}_n\right)\right\}_{n=1}^N=\mathcal{F}\left(\mathbf{I}_s, \mathbf{D}_s\right) {(cn?,σn?,dn?)}n=1N?=F(Is?,Ds?)

其中 ${\mathbf{I}}_s$ 和 ${\mathbf{D}}_s$ 分别是原始视角 $s$ 下的图像和深度，$N$ 是一个预定义的参数，表示 MPI 中的平面数量。

因此，新视角下图像平面上的每个像素 $(x_t,y_t)$ 都可以通过同源函数[映射到第 $n$ 个源 MPI 平面上的像素 $(x_s,y_s)$：

${\left[x_s,y_s,1\right]}^T～\mathbf{K}\left(\mathbf{R}?\frac{{\mathbf{tn}}^T}{{\mathbf{d}}_n}\right){\mathbf{K}}^{?1}{\left[x_t,y_t,1\right]}^T$

其中，$\mathbf{R}$ 和 $\mathbf{t}$ 为从源视角到目标视角的旋转和平移矩阵，$K$ 为相机固有内参，$\mathbf{n}=[0,0,1]$ 为法向量。因此，每个新平面的颜色和密度可以通过双线性采样得到。然后我们使用新平面和通过场景的任意光线之间的离散交点来估计积分：

${\mathbf{I}}_t={\sum }_{n=1}^N\left({\mathbf{c}}_n^{\prime }{\mathbf{\alpha }}_n^{\prime }{\prod }_{m=1}^{n?1}\left(1?{\mathbf{\alpha }}_m^{\prime }\right)\right)$

其中 ${\mathbf{\alpha }}_n^{\prime }=\exp \left(?{\mathbf{\delta }}_n{\mathbf{\sigma }}_n^{\prime }\right)$，${\mathbf{\delta }}_n$ 是平面 $n$ 和 $n+1$ 之间的距离映射。

虽然基于mpi的方法可以合成真实的图像，但也需要可靠的光流图来训练基于学习的光流估计模型。因此，我们建议在每个平面上增加一个额外的光通道。

为此，我们计算了源图像在像素为 $(x_s,y_s)$ 处的第 n 个平面上的光流为：

${\mathbf{f}}_n=\left[x_t?x_s,y_t?y_s\right]$

通过用反等价形式的向后 Warp 过程：

${\left[x_t,y_t,1\right]}^T～\mathbf{K}\left({\mathbf{R}}^{?}?\frac{{\mathbf{t}}^{?}{\mathbf{n}}^T}{{\mathbf{d}}_n}\right){\mathbf{K}}^{?1}{\left[x_s,y_s,1\right]}^T$

为了确保光流图与新的视图图像完美匹配，我们建议同样用体积渲染获取最终的光流标签：

${\mathbf{F}}_{s\to t}={\sum }_{n=1}^N\left({\mathbf{f}}_n{\mathbf{\alpha }}_n{\prod }_{m=1}^{n?1}\left(1?{\mathbf{\alpha }}_m\right)\right)$

Independent Object Motions

为了模拟更真实的运动，我们建议应用从场景中提取的对象和静态背景的虚拟运动。因此，我们利用实例分割网络提取源图像中的主对象掩码。

然后，分别对背景和前景使用不同的相机运动，来模拟运动场场景。

如图所示，在添加独立运动前，物体和场景有相似的光流，因为他们运动方向保持一致。

添加独立运动后，物体跟场景有了分离的运动方向，更符合真实场景运动。

Depth-Aware Inpainting

虽然合并后的图像具有真实的视觉效果，但由摄像机运动和物体运动引起的深度变化也会导致非自然的遮挡。为了解决这个问题，我们使用体积渲染来获得场景新视图的深度：

${\mathbf{D}}_t={\sum }_{n=1}^N\left({\mathbf{d}}_n^{\prime }{\mathbf{\alpha }}_n^{\prime }{\prod }_{m=1}^{n?1}\left(1?{\mathbf{\alpha }}_m^{\prime }\right)\right)$

用同样的方法也可以得到物体新视角的深度。然后，我们利用这两个深度来计算新视图之间的占据掩模，并修复物体和场景的前后遮挡关系，如图所示：

实验结果：

为了评估所提出方法的有效性，MPI-Flow 在广泛使用的真实光流数据集上进行了实验：KITTI 数据集，并测试了不同来源的原始单目图像数据对结果的影响。

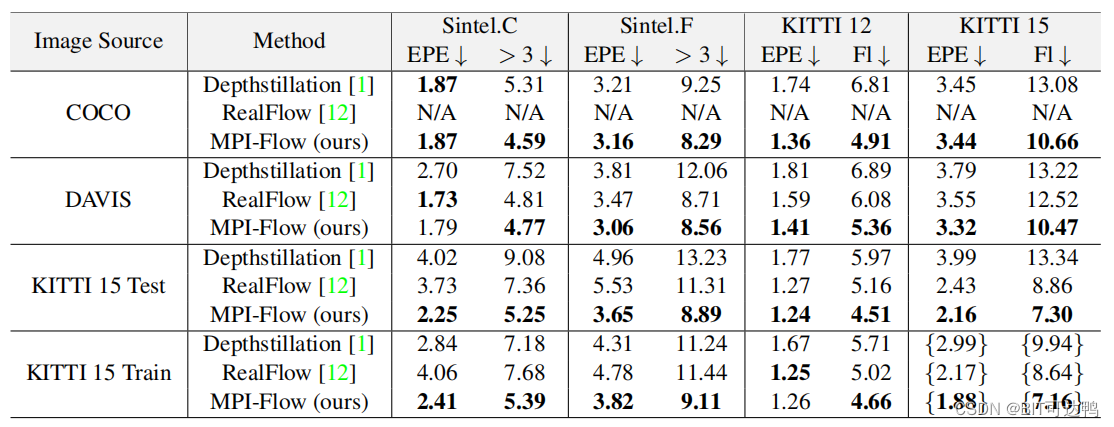
表一给出了交叉数据集的验证结果，以及与其他来自真实图像或视频的数据集生成方法的比较。“Image Source”列表示用于光流训练数据生成的图像数据集。报告了使用不同方法在不同数据集上训练的 RAFT 的评价结果（使用 C+T 进行预训练）。鉴于 RealFlow 无法处理来自 COCO 的单视图图像，该结果标注为“N/A。花括号“{}”表示对未标记的评估集的使用，这个表中表示 KITTI 15 训练集。

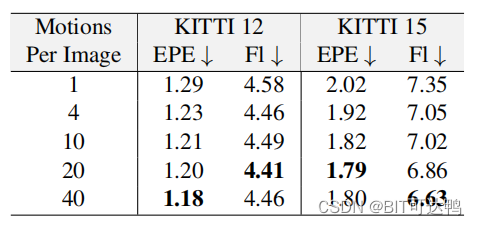
消融实验表明，在原始图像数量相同的情况下，使用更多的随机运动合成更多数据，有助于进一步提高性能。