回溯法:0-1背包问题

问题描述

给定种物品和一背包。 物品的重量是， 其价值为，背包的容量为 c。 问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？注意物品不重复!

实例：物品价值V={12, 11, 9, 8}, 物品重量W={8, 6, 4, 3}, 背包容量c=13

结点：向量 （ 子集的部分特征向量）

搜索空间： 子集树，片树叶

其中两个可行解为：

回溯法模版回顾?

参考文章：代码随想录

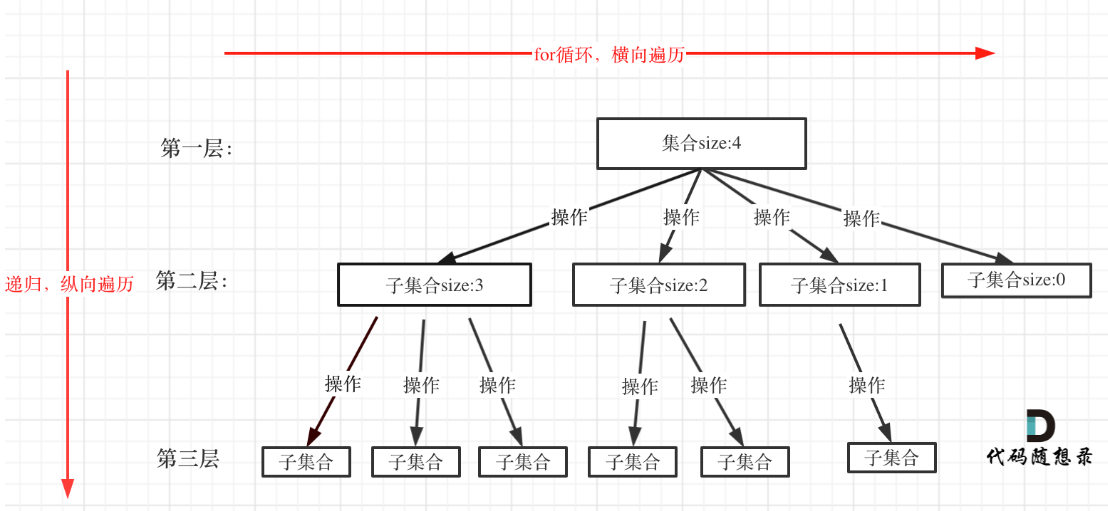
回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

实现代码

终止条件代码

public static void backtracking(int n,  int startIndex) {
    if (startIndex>=n){
        //此时startIndex越界了
        if (getPathSum()<=c){
            result.add(new ArrayList<>(path));
            return;
        }
        return;
    }
    //再加后面任意一个就肯定不够了
    if (getPathSum()<=c&&(getPathSum() + items_min_weight[startIndex]) > c) {
        //        if (getPathSum()<c) {
        result.add(new ArrayList<>(path));
        return;
    }
    for (int i = startIndex; i < n; i++) {
        path.add(i);
        backtracking(n,  i + 1);
        path.removeLast();
    }

最终代码(含注释)

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

public class KnapsackProblem {
    static List<List<Integer>> result = new ArrayList<>();
    static LinkedList<Integer> path = new LinkedList<>();

    static int N = 4;
    //    static int[] items_weight = new int[N];
    static int[] items_weight = {8, 6, 4, 3};
    //    static int[] items_value = new int[N];
    static int[] items_value = {12, 11, 9, 8};
    //每个items_min_weight(对应下标为i)的值为min{items_weight[i],...,items_weight[N-1]}
    static int[] items_min_weight = new int[N];
    //c为背包的容量
    static int c=13;

    public static void main(String[] args) {
        items_min_weight[N - 1] = items_weight[N - 1];
        int min = items_min_weight[N - 1];
        for (int i = items_weight.length - 2; i >= 0; i--) {
            if (items_weight[i] < min) {
                min = items_weight[i];
            }
            items_min_weight[i] = min;
        }
        backtracking(N,  0);
        System.out.println("可行解有:");
        result.forEach(System.out::println);
        //要是想求最优解,直接对每个可行解对应重量求和,之后取最大一个就好啦
    }

    public static void backtracking(int n,  int startIndex) {
        if (startIndex>=n){
            //此时startIndex越界了
            if (getPathSum()<=c){
                result.add(new ArrayList<>(path));
                return;
            }
            return;
        }
        //再加后面任意一个就肯定不够了
        if (getPathSum()<=c&&(getPathSum() + items_min_weight[startIndex]) > c) {
            //        if (getPathSum()<c) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < n; i++) {
            path.add(i);
            backtracking(n,  i + 1);
            path.removeLast();
        }
    }

    public static int getPathSum() {
        int sum = 0;
        for (int i = 0; i < path.size(); i++) {
            sum += items_weight[path.get(i)];
        }
        return sum;
    }
}