TCN 时序卷积网络 （temporal convolutional network）【因果卷积、空洞卷积】

TCN 时序卷积 （temporal convolutional network）

它由膨胀卷积核因果卷积两种卷积构成。

如图：左边是膨胀因果卷积，右边是1x1卷积构成的残差连接，两条链路并行，构成残差块，残差块在串联构成时序卷积神经网络。

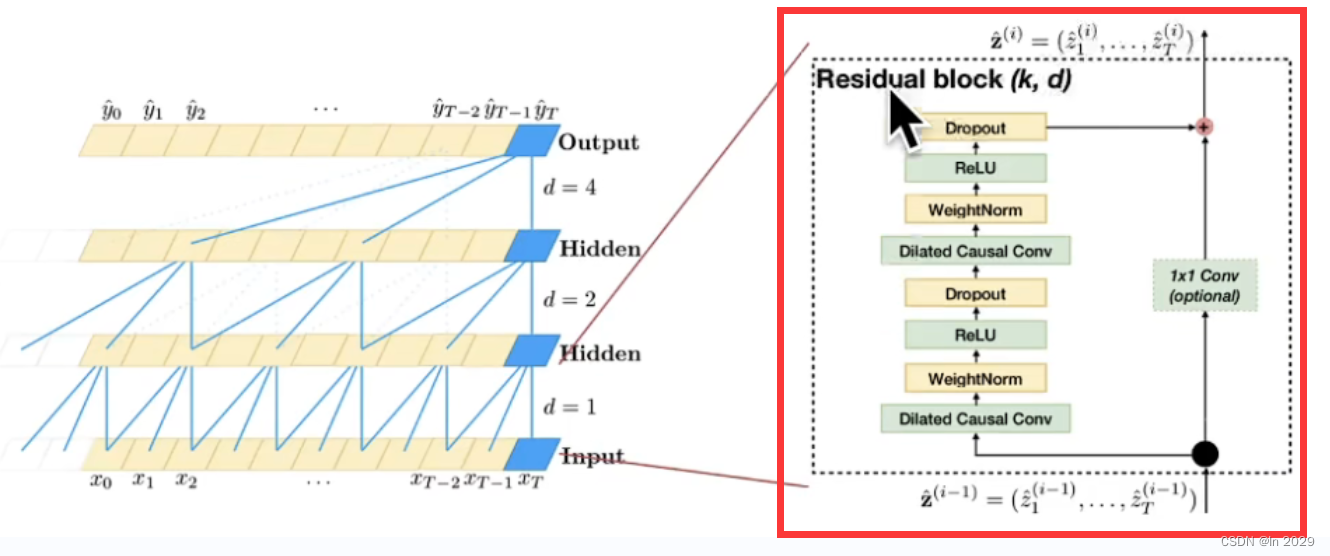
1.因果卷积

在深度学习中，卷积是一个常见的操作。但在处理时间序列数据时，特别是在预测未来的时刻，我们不希望未来的信息在当前时刻被使用。但是在一维卷积的计算过程中，很显然我们会涉及到的不止过去的时间点，还有未来的时间点（即不止会涉及到上方的样本，还会涉及到下方的样本）

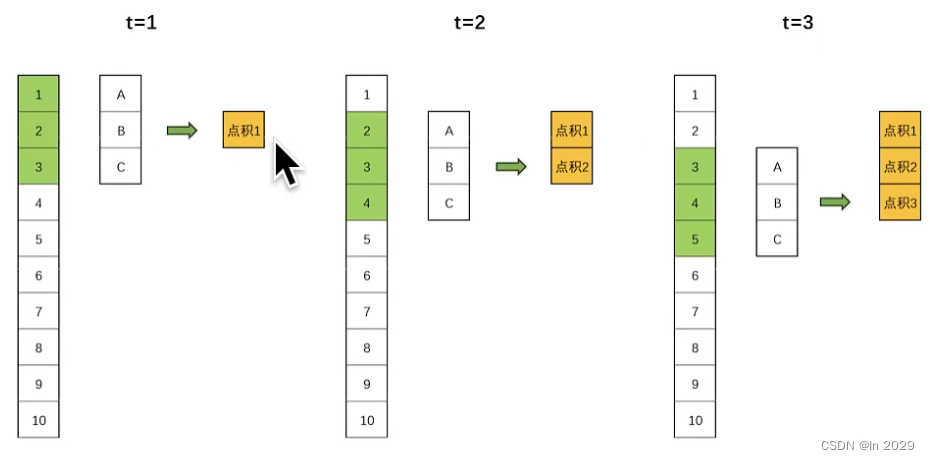
这就引入了“因果卷积”。因果卷积保证了在任何时间点t，输出只依赖于时间点t及其之前的输入，而不依赖于t之后的输入。因果卷积可以通过对输入数据进行适当的“填充”来实现。具体地说，假设我们有一个一维的输入序列和一个大小为k的卷积核，为了实现因果卷积，我们可以在序列的开始处填充k-1个零，然后进行标准的卷积操作。这样，卷积的输出在任何时间点t都会依赖于时间点t及其之前的输入，如下图：

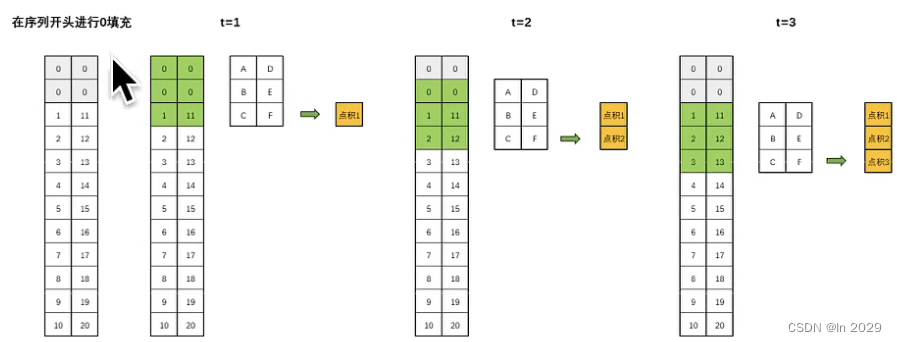
2.膨胀卷积

（1）膨胀卷积也叫空洞卷积、扩张卷积。最初的提出是为了解决图像分割的问题，常见的图像分割算法通常使用池化层和卷 积层来增加感受野，同时也缩小了特征图尺寸，然后利用上采样还原图像尺寸，特征图缩小在放大的过程造成了精度上的损失，因此需要一种操作可以在增加感受野的同时保持特征图的尺寸不变，从而代替下采样和上采样操作。

（2）感受野：指特征图上的某个点能看到的输入图像的区域，即特征图上的点是由输入图像中感受野大小区域的计算得到。如下图

（3）计算当前层感受野的公式：
$$R{F}_{i+1}=R{F}_i+(k?1)\times S_i$$
? 其中，$R{F}_{i+1}$表示当前层的感受野，$R{F}_i$表示上一层的感受野，k表示卷积核的大小，$S_i$表示之前所有层的步长的乘积（不包含本层）

（4）膨胀卷积的原理：

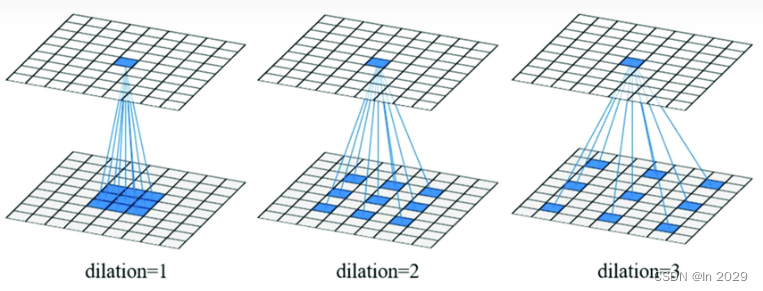
? 与正常的卷积不同的是，膨胀卷积引入了“扩张率”的超参数，该超参数定义了卷积核处理数据时各值的间距。

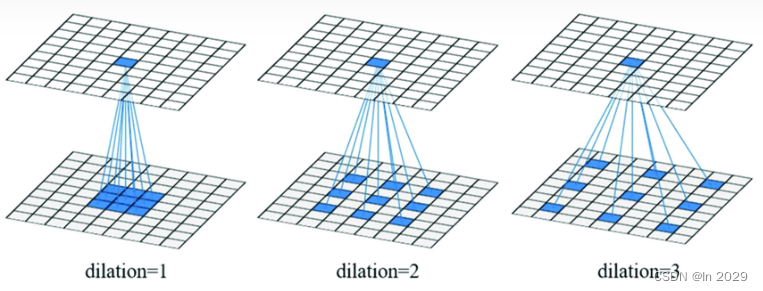
dilation = 1,卷积后的感受野为3；

dilation = 2,卷积后的感受野为5；

dilation = 3,卷积后的感受野为7；

（5）理解膨胀卷积可以增大感受野，但是可以不改变图像输出特征图的尺寸。

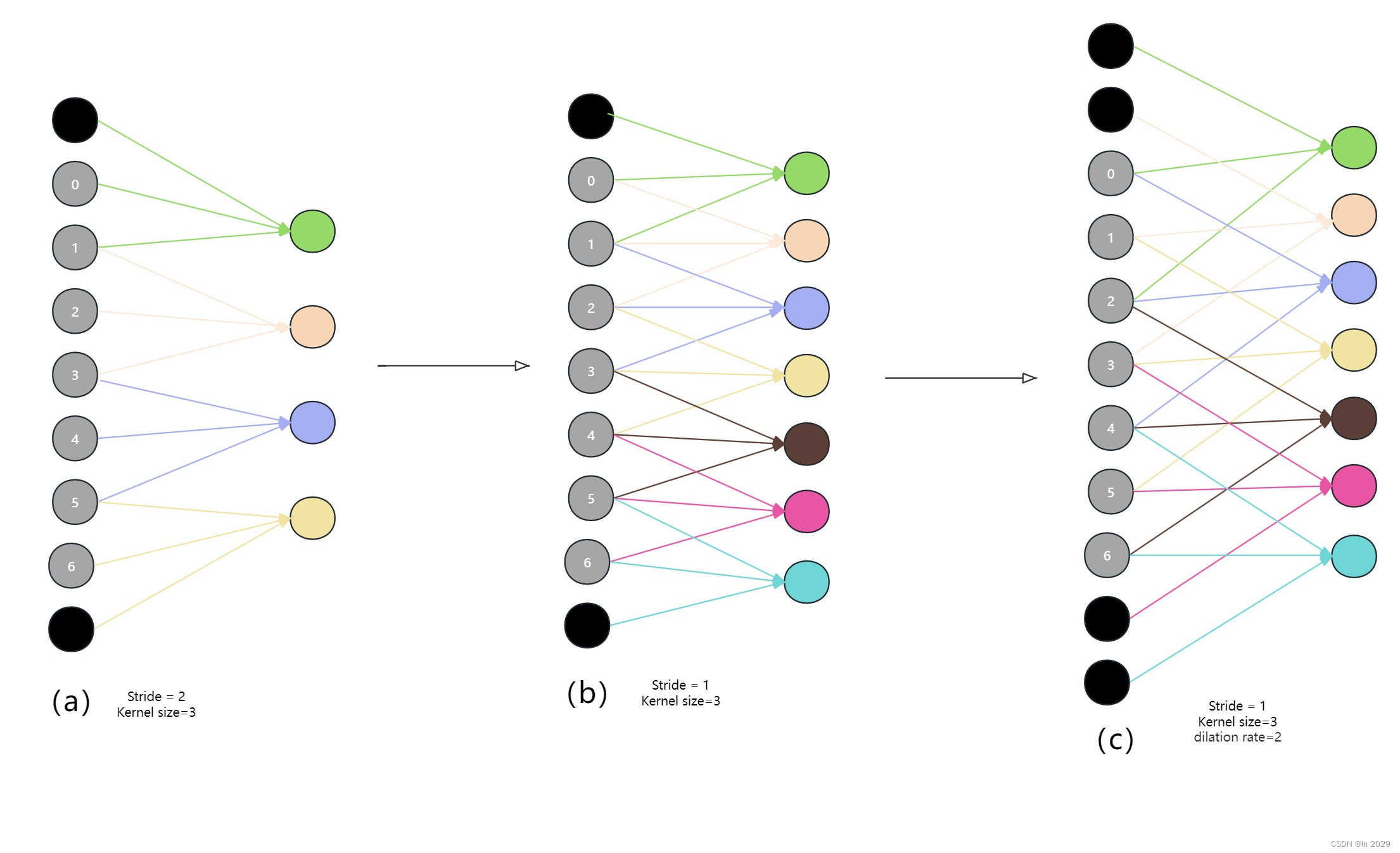
从b和c可以看出，有无膨胀卷积，不影响输出特征的尺寸，但是利用膨胀卷积可以增大感受野

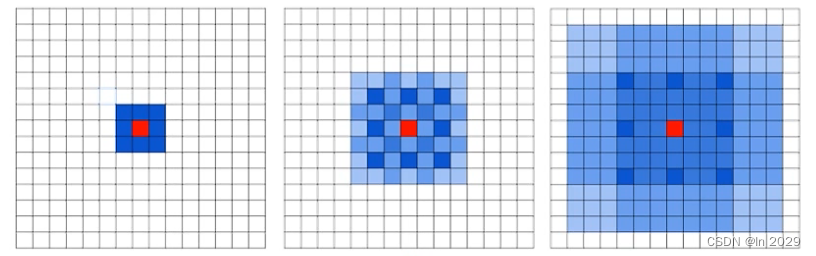
（6）存在的问题：The Gridding Effect

如果多次叠加 dilation rate=2 d 3 x 3 卷积核，会出现以下问题

如图可以看到，很多像素点没有被覆盖到。

（7）解决方法：Hybrid Dilated Convolution (HDC)

假设连续堆叠 N 个空洞卷积，然后卷积核大小为 K x K 膨胀卷积系数分别为 [r1,r2,r3,…,rn],想要设计出一个没有间隙的区域，需要满足以下特性：

特性1：叠加卷积的系数不能有大于1的公约数；

特性2：卷积的系数成锯齿状结构，如[1,2,5,1,2,51,2,5]

特性3：满足下列式子
$$M_i=\max [M_{i+1}?2r_i,M_{i+1}?2(M_{i+1}?r_i),r_i]$$
其中$r_i$是是 i 层的 dilation rate 而 $M_i$是指在 i 层的最大dilation rate，那么假设总共有n层的话， 默认$M_n$=$r_n$。假设我们应用于 kernel 为 k x k 的话，我们的目标则是$M_2$≤k,这样我们至少可以用dilation rate=1的方式来覆盖所有。

???????????????????????????????????????????
我是韩一，用知识认识更多的人，欢迎大家指正！